
Time evolution
Encyclopedia
Time evolution is the change of state brought about by the passage of time
, applicable to systems with internal state (also called stateful systems). In this formulation, time is not required to be a continuous parameter, but may be discrete
or even finite. In classical physics
, time evolution of a collection of rigid bodies
is governed by the principles of classical mechanics
. In their most rudimentary form, these principles express the relationship between forces acting on the bodies and their acceleration given by Newton's laws of motion
. These principles can also be equivalently expressed more abstractly by Hamiltonian mechanics
or Lagrangian mechanics
.
The concept of time evolution may be applicable to other stateful systems as well. For instance, the operation of a Turing machine
can be regarded as the time evolution of the machine's control state together with the state of the tape (or possibly multiple tapes) including the position of the machine's read-write head (or heads). In this case, time is discrete.
Stateful systems often have dual descriptions in terms of states or in terms of observable
values. In such systems, time evolution can also refer to the change in observable values. This is particularly relevant in quantum mechanics
where the Schrödinger picture
and Heisenberg picture
are (mostly) equivalent descriptions of time evolution.
s R. Then time evolution is given by a family of bijective state transformations
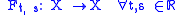
Ft, s(x) is the state of the system at time t, whose state at time s is x. The following identity holds
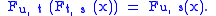
To see why this is true, suppose x ∈ X is the state at time s. Then by the definition of F, Ft, s(x) is the state of the system at time t and consequently applying the definition once more, Fu, t(Ft, s(x)) is the state at time u. But this is also Fu, s(x).
In some contexts in mathematical physics, the mappings Ft, s are called propagation operators or simply propagator
s. In classical mechanics
, the propagators are functions that operate on the phase space
of a physical system. In quantum mechanics
, the propagators are usually unitary operator
s on a Hilbert space
. The propagators can be expressed as time-ordered exponentials of the integrated Hamiltonian. The asymptotic properties of time evolution are given by the scattering matrix.
A state space with a distinguished propagator is also called a dynamical system
.
To say time evolution is homogeneous means that
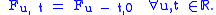
In the case of a homogeneous system, the mappings Gt = Ft,0 form a one-parameter group
of transformations of X, that is

Non-reversibility. For non-reversible systems, the propagation operators Ft, s are defined whenever t ≥ s and satisfy the propagation identity
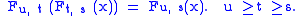
In the homogeneous case the propagators are exponentials of the Hamiltonian.
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
, applicable to systems with internal state (also called stateful systems). In this formulation, time is not required to be a continuous parameter, but may be discrete
Discrete time
Discrete time is the discontinuity of a function's time domain that results from sampling a variable at a finite interval. For example, consider a newspaper that reports the price of crude oil once every day at 6:00AM. The newspaper is described as sampling the cost at a frequency of once per 24...
or even finite. In classical physics
Classical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
, time evolution of a collection of rigid bodies
Rigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
is governed by the principles of classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
. In their most rudimentary form, these principles express the relationship between forces acting on the bodies and their acceleration given by Newton's laws of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
. These principles can also be equivalently expressed more abstractly by Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
or Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
.
The concept of time evolution may be applicable to other stateful systems as well. For instance, the operation of a Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
can be regarded as the time evolution of the machine's control state together with the state of the tape (or possibly multiple tapes) including the position of the machine's read-write head (or heads). In this case, time is discrete.
Stateful systems often have dual descriptions in terms of states or in terms of observable
Observable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
values. In such systems, time evolution can also refer to the change in observable values. This is particularly relevant in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
where the Schrödinger picture
Schrödinger picture
In physics, the Schrödinger picture is a formulation of quantum mechanics in which the state vectors evolve in time, but the operators are constant. This differs from the Heisenberg picture which keeps the states constant while the observables evolve in time...
and Heisenberg picture
Heisenberg picture
In physics, the Heisenberg picture is a formulation of quantum mechanics in which the operators incorporate a dependency on time, but the state vectors are time-independent. It stands in contrast to the Schrödinger picture in which the operators are constant and the states evolve in time...
are (mostly) equivalent descriptions of time evolution.
Time evolution operators
Consider a system with state space X for which evolution is deterministic and reversible. For concreteness let us also suppose time is a parameter that ranges over the set of real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s R. Then time evolution is given by a family of bijective state transformations
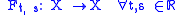
Ft, s(x) is the state of the system at time t, whose state at time s is x. The following identity holds
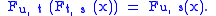
To see why this is true, suppose x ∈ X is the state at time s. Then by the definition of F, Ft, s(x) is the state of the system at time t and consequently applying the definition once more, Fu, t(Ft, s(x)) is the state at time u. But this is also Fu, s(x).
In some contexts in mathematical physics, the mappings Ft, s are called propagation operators or simply propagator
Propagator
In quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...
s. In classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, the propagators are functions that operate on the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
of a physical system. In quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the propagators are usually unitary operator
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
s on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. The propagators can be expressed as time-ordered exponentials of the integrated Hamiltonian. The asymptotic properties of time evolution are given by the scattering matrix.
A state space with a distinguished propagator is also called a dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
.
To say time evolution is homogeneous means that
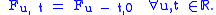
In the case of a homogeneous system, the mappings Gt = Ft,0 form a one-parameter group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of transformations of X, that is

Non-reversibility. For non-reversible systems, the propagation operators Ft, s are defined whenever t ≥ s and satisfy the propagation identity
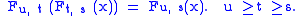
In the homogeneous case the propagators are exponentials of the Hamiltonian.

