
Path decomposition
Encyclopedia
In graph theory
, a path decomposition of a graph G is, informally, a representation of G as a "thickened" path graph
, and the pathwidth of G is a number that measures how much the path was thickened to form G. More formally, a path-decomposition is
a sequence of subsets of vertices of G such that the endpoints of each edge appear in one of the subsets and such that each vertex appears in a contiguous subsequence of the subsets, and the pathwidth is one less than the size of the largest set in such a decomposition.
Pathwidth is also known as interval thickness (one less than the maximum clique size in an interval
supergraph of G), vertex separation number, or node searching number.
Pathwidth and path-decompositions are closely analogous to treewidth and tree decomposition
s. They play a key role in the theory of graph minors: the families of graphs that are closed under graph minors and do not include all forest
s may be characterized as having bounded pathwidth, and the "vortices" appearing in the general structure theory for minor-closed graph families
have bounded pathwidth. Pathwidth, and graphs of bounded pathwidth, also have applications in VLSI design, graph drawing
, and computational linguistics
.
It is NP-hard
to find the pathwidth of arbitrary graphs, or even to approximate it accurately. However, the problem is fixed-parameter tractable: testing whether a graph has pathwidth k can be solved in an amount of time that depends linearly on the size of the graph but superexponentially on k. Additionally, for several special classes of graphs, such as trees
, the pathwidth may be computed in polynomial time without dependence on k.
Many problems in graph algorithms may be solved efficiently on graphs of bounded pathwidth, by using dynamic programming
on a path-decomposition of the graph. Path decomposition may also be used to measure the space complexity of dynamic programming algorithms on graphs of bounded treewidth.
The second of these two properties is equivalent to requiring that the subsets containing any particular vertex form a contiguous subsequence of the whole sequence. In the language of the later papers in Robertson and Seymour's graph minor series, a path-decomposition is a tree decomposition
(X,T) in which the underlying tree T of the decomposition is a path graph
.
The width of a path-decomposition is defined in the same way as for tree-decompositions, as maxi |Xi| − 1, and the pathwidth of G is the minimum width of any path-decomposition of G. The subtraction of one from the size of Xi in this definition makes little difference in most applications of pathwidth, but is used to make the pathwidth of a path graph
be equal to one.
 The pathwidth of any graph G is equal to one less than the smallest clique number of an interval graph
The pathwidth of any graph G is equal to one less than the smallest clique number of an interval graph
that contains G as a subgraph. That is, for every path decomposition of G one can find an interval supergraph of G, and for every interval supergraph of G one can find a path decomposition of G, such that the width of the decomposition is one less than the clique number of the interval graph.
In one direction, suppose a path decomposition of G is given. Then one may represent the nodes of the decomposition as points on a line (in path order) and represent each vertex v as a closed interval having these points as endpoints. In this way, the path decomposition nodes containing v correspond to the representative points in the interval for v. The intersection graph
of the intervals formed from the vertices of G is an interval graph that contains G as a subgraph. Its maximal cliques are given by the sets of intervals containing the representative points, and its maximum clique size is one plus the pathwidth of G.
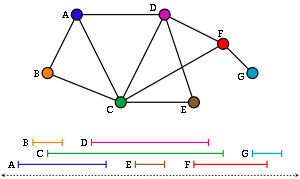
In the other direction, if G is a subgraph of an interval graph with clique number p + 1, then G has a path decomposition of width p whose nodes are given by the maximal cliques of the interval graph. For instance, the interval graph shown with its interval representation in the figure has a path decomposition with five nodes, corresponding to its five maximal cliques ABC, ACD, CDE, CDF, and FG; the maximum clique size is three and the width of this path decomposition is two.
This equivalence between pathwidth and interval thickness is closely analogous to the equivalence between treewidth and the minimum clique number (minus one) of a chordal graph
of which the given graph is a subgraph. Interval graphs are a special case of chordal graphs, and chordal graphs can be represented as intersection graphs of subtrees of a common tree generalizing the way that interval graphs are intersection graphs of subpaths of a path.
The vertex separation number of G is the minimum vertex separation number of any linear ordering of G. The vertex separation number was defined by , and is equal to the pathwidth of G.
This follows from the earlier equivalence with interval graph clique numbers: if G is a subgraph of an interval graph I, represented (as in the figure) in such a way that all interval endpoints are distinct, then the ordering of the left endpoints of the intervals of I has vertex separation number one less than the clique number of I. And in the other direction, from a linear ordering of G one may derive an interval representation in which the left endpoint of the interval for a vertex v is its position in the ordering and the right endpoint is the position of the neighbor of v that comes last in the ordering.
in which a set of searchers collaborate to track down a fugitive hiding in a graph. The searchers are placed on vertices of the graph while the fugitive may be in any edge of the graph, and the fugitive's location and moves are hidden from the searchers. In each turn, some or all of the searchers may move (arbitrarily, not necessarily along edges) from one vertex to another, and then the fugitive may move along any path in the graph that does not pass through a searcher-occupied vertex. The fugitive is caught when both endpoints of his edge are occupied by searchers. The node searching number of a graph is the minimum number of searchers needed to ensure that the fugitive can be guaranteed to be caught, no matter how he moves. As show, the node searching number of a graph equals its interval thickness. The optimal strategy for the searchers is to move the searchers so that in successive turns they form the separating sets of a linear ordering with minimal vertex separation number.
pathwidth-k graphs (graphs to which no more edges can be added without increasing the pathwidth) have exactly this many edges. A maximal pathwidth-k graph must be either a k-path or a k-caterpillar, two special kinds of k-tree. A k-tree is a chordal graph
with exactly maximal cliques, each containing vertices; in a k-tree that is not itself a , each maximal clique either separates the graph into two or more components, or it contains a single leaf vertex, a vertex that belongs to only a single maximal clique. A k-path is a k-tree with at most two leaves, and a k-caterpillar is a k-tree in which the non-leaf vertices induce a k-path. In particular the maximal graphs of pathwidth one are exactly the caterpillar tree
s.
Since path-decompositions are a special case of tree-decompositions, the pathwidth of any graph is greater than or equal to its treewidth. The pathwidth is also less than or equal to the cutwidth, the minimum number of edges that crosses any cut between lower-numbered and higher-numbered vertices in an optimal linear arrangement of the vertices of a graph; this follows because the vertex separation number, the number of lower-numbered vertices with higher-numbered neighbors, can at most equal the number of cut edges. For similar reasons, the cutwidth is at most the pathwidth times the maximum degree
of the vertices in a given graph.
Any n-vertex forest
has pathwidth O(log n). For, in a forest, one can always find a constant number of vertices the removal of which leaves a forest that can be partitioned into two smaller subforests with at most 2n/3 vertices each. A linear arrangement formed by recursively partitioning each of these two subforests, placing the separating vertices between them, has logarithmic vertex searching number. The same technique, applied to a tree-decomposition of a graph, shows that, if the treewidth of an n-vertex graph G is t, then the pathwidth of G is O(t log n). Since outerplanar graph
s, series-parallel graph
s, and Halin graph
s all have bounded treewidth, they all also have at most logarithmic pathwidth.
As well as its relations to treewidth, pathwidth is also related to clique-width
and cutwidth, via line graph
s; the line graph L(G) of a graph G has a vertex for each edge of G and two vertices in L(G) are adjacent when the corresponding two edges of G share an endpoint. Any family of graphs has bounded pathwidth if and only if its line graphs have bounded linear clique-width, where linear clique-width replaces the disjoint union operation from clique-width with the operation of adjoining a single new vertex. If a connected graph with three or more vertices has maximum degree three, then its cutwidth equals the vertex separation number of its line graph.
In any planar graph
, the pathwidth is at most proportional to the square root of the number of vertices. One way to find a path-decomposition with this width is (similarly to the logarithmic-width path-decomposition of forests described above) to use the planar separator theorem
to find a set of O(√n) vertices the removal of which separates the graph into two subgraphs of at most 2n/3 vertices each, and concatenate recursively-constructed path decompositions for each of these two subgraphs. The same technique applies to any class of graphs for which a similar separator theorem holds. Since, like planar graphs, the graphs in any fixed minor-closed graph family have separators of size O(√n), it follows that the pathwidth of the graphs in any fixed minor-closed family is again O(√n). For some classes of planar graphs, the pathwidth of the graph and the pathwidth of its dual graph
must be within a constant factor of each other: bounds of this form are known for biconnected outerplanar graphs and for polyhedral graphs. For 2-connected planar graphs, the pathwidth of the dual graph less than the pathwidth of the line graph. It remains open whether the pathwidth of a planar graph and its dual are always within a constant factor of each other in the remaining cases.
In some classes of graphs, it has been proven that the pathwidth and treewidth are always equal to each other: this is true for cograph
s, permutation graph
s, the complements
of comparability graph
s, and the comparability graphs of interval order
s.
In any cubic graph
, or more generally any graph with maximum vertex degree three, the pathwidth is at most n/6 + o(n), where n is the number of vertices in the graph. There exist cubic graphs with pathwidth 0.082n, but it is not known how to reduce this gap between this lower bound and the n/6 upper bound.
to determine whether the pathwidth of a given graph is at most k, when k is a variable given as part of the input. The best known worst-case time bounds for computing the pathwidth of arbitrary n-vertex graphs are of the form O(2n nc) for some constant c. Nevertheless several algorithms are known to compute path-decompositions more efficiently when the pathwidth is small, when the class of input graphs is limited, or approximately.
algorithm is applied to this decomposition in order to find the optimal decomposition.
However, the time bounds for known algorithms of this type are exponential in k2, impractical except for the smallest values of k. For the case k = 2 an explicit linear-time algorithm based on a structural decomposition of pathwidth-2 graphs is given by .
s, planar graphs of bounded degree, chordal graph
s, chordal dominoes, the complements
of comparability graph
s,,
and bipartite
distance-hereditary graph
s. It follows immediately that it is also NP-complete for the graph families that contain the bipartite distance-hereditary graphs, including the bipartite graphs, chordal bipartite graphs, distance-hereditary graphs, and circle graph
s.
However, the pathwidth may be computed in linear time for trees and forests, and for graphs of bounded treewidth including series-parallel graph
s, outerplanar graph
s, and Halin graph
s. It may also be computed in polynomial time for split graph
s, for the complements of chordal graphs, for permutation graph
s, for cograph
s, for circular-arc graph
s, for the comparability graphs of interval orders, and of course for interval graph
s themselves, since in that case the pathwidth is just one less than the maximum number of intervals covering any point in an interval representation of the graph.
The best known approximation ratio of a polynomial time approximation algorithm for pathwidth is O((log n)3/2).
For earlier approximation algorithms for pathwidth, see and . For approximations on restricted classes of graphs, see .
F can be characterized as the graphs that do not have any minor in X, where X is a finite set of forbidden minors. For instance, Wagner's theorem states that the planar graph
s are the graphs that have neither the complete graph
K5 nor the complete bipartite graph
K3,3 as minors. In many cases, the properties of F and the properties of X are closely related, and the first such result of this type was by , and relates bounded pathwidth with the existence of a forest
in the family of forbidden minors. Specifically, define a family F of graphs to have bounded pathwidth if there exists a constant p such that every graph in F has pathwidth at most p. Then, a minor-closed family F has bounded pathwidth if and only if the set X of forbidden minors for F includes at least one forest.
In one direction, this result is straightforward to prove: if X does not include at least one forest, then the X-minor-free graphs do not have bounded pathwidth. For, in this case, the X-minor-free graphs include must all forests, and in particular they include the perfect binary trees. But a perfect binary tree with k levels has pathwidth k − 1, so in this case the X-minor-free-graphs have unbounded pathwidth. In the other direction, if X contains an n-vertex forest, then the X-minor-free graphs have pathwidth at most n − 2.
Although Xp necessarily includes at least one forest, it is not true that all graphs in Xp are forests: for instance, X1 consists of two graphs, a seven-vertex tree and the triangle K3. However, the set of trees in Xp may be precisely characterized: these trees are exactly the trees that can be formed from three trees in Xp − 1 by connecting a new root vertex by an edge to an arbitrarily chosen vertex in each of the three smaller trees. For instance, the seven-vertex tree in X1 is formed in this way from the two-vertex tree (a single edge) in X0. Based on this construction, the number of forbidden minors in Xp can be shown to be at least (p!)2. The complete set X2 of forbidden minors for pathwidth-2 graphs has been computed; it contains 110 different graphs.
for minor-closed graph families states that, for any such family F, the graphs in F can be decomposed into clique-sum
s of graphs that can be embedded
onto surfaces of bounded genus
, together with a bounded number of apexes and vortices for each component of the clique-sum. An apex is a vertex that may be adjacent to any other vertex in its component, while a vortex is a graph of bounded pathwidth that is glued into one of the faces of the bounded-genus embedding of a component. The cyclic ordering of the vertices around the face into which a vortex is embedded must be compatible with the path decomposition of the vortex, in the sense that breaking the cycle to form a linear ordering must lead to an ordering with bounded vertex separation number. This theory, in which pathwidth is intimately connected to arbitrary minor-closed graph families, has important algorithmic applications.
use interval thickness to model the number of tracks needed in a one-dimensional layout of a VLSI circuit, formed by a set of modules that need to be interconnected by a system of nets. In their model, one forms a graph in which the vertices represent nets, and in which two vertices are connected by an edge if their nets both connect to the same module; that is, if the modules and nets are interpreted as forming the nodes and hyperedges of a hypergraph
then the graph formed from them is its line graph. An interval representation of a supergraph of this line graph, together with a coloring
of the supergraph, describes an arrangement of the nets along a system of horizontal tracks (one track per color) in such a way that the modules can be placed along the tracks in a linear order and connect to the appropriate nets. The fact that interval graphs are perfect graph
s implies that the number of colors needed, in an optimal arrangement of this type, is the same as the clique number of the interval completion of the net graph.
Gate matrix layout is a specific style of CMOS
VLSI layout for Boolean logic
circuits. In gate matrix layouts, signals are propagated along "lines" (vertical line segments) while each gate of the circuit is formed by a sequence of device features that lie along a horizontal line segment. Thus, the horizontal line segment for each gate must cross the vertical segments for each of the lines that form inputs or outputs of the gate. As in the layouts of , a layout of this type that minimizes the number of vertical tracks on which the lines are to be arranged can be found by computing the pathwidth of a graph that has the lines as its vertices and pairs of lines sharing a gate as its edges. The same algorithmic approach can also be used to model folding problems in programmable logic array
s.
:
of high-level programming language
s, pathwidth arises in the problem of reordering sequences of straight-line code (that is, code with no control flow
branches or loops) in such a way that all the values computed in the code can be placed in machine registers
instead of having to be spilled into main memory. In this application, one represents the code to be compiled as a directed acyclic graph
in which the nodes represent the input values to the code and the values computed by the operations within the code. An edge from node x to node y in this DAG represents the fact that value x is one of the inputs to operation y. A topological ordering of the vertices of this DAG represents a valid reordering of the code, and the number of registers needed to evaluate the code in a given ordering is given by the vertex separation number of the ordering.
For any fixed number w of machine registers, it is possible to determine in linear time whether a piece of straight-line code can be reordered in such a way that it can be evaluated with at most w registers. For, if the vertex separation number of a topological ordering is at most w, the minimum vertex separation among all orderings can be no larger, so the undirected graph formed by ignoring the orientations of the DAG described above must have pathwith at most w. It is possible to test whether this is the case, using the known fixed-parameter-tractable algorithms for pathwidth, and if so to find a path-decomposition for the undirected graph, in linear time given the assumption that w is a constant. Once a path decomposition has been found, a topological ordering of width w (if one exists) can be found using dynamic programming, again in linear time.
. In this application, sentences are modeled as graphs, in which the vertices represent words and the edges represent relationships between words; for instance if an adjective modifies a noun in the sentence then the graph would have an edge between those two words. Due to the limited capacity of human short-term memory, Kornai and Tuza argue that this graph must have bounded pathwidth (more specifically, they argue, pathwidth at most six), for otherwise humans would not be able to parse speech correctly.
on a path-decomposition of the graph. For instance, if a linear ordering of the vertices of an n-vertex graph G is given, with vertex separation number w, then it is possible to find the maximum independent set of G in time On graphs of bounded pathwidth, this approach leads to fixed-parameter tractable algorithms, parametrized by the pathwidth. Such results are not frequently found in the literature because they are subsumed by similar algorithms parametrized by the treewidth; however, pathwidth arises even in treewidth-based dynamic programming algorithms in measuring the space complexity of these algorithms.
The same dynamic programming method also can be applied to graphs with unbounded pathwidth, leading to algorithms that solve unparametrized graph problems in exponential time. For instance, combining this dynamic programming approach with the fact that cubic graphs have pathwidth n/6 + o(n) shows that, in a cubic graph, the maximum independent set can be constructed in time O(2n/6 + o(n)), faster than previous known methods. A similar approach leads to improved exponential-time algorithms for the maximum cut
and minimum dominating set problems in cubic graphs, and for several other NP-hard optimization problems.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a path decomposition of a graph G is, informally, a representation of G as a "thickened" path graph
Path graph
In the mathematical field of graph theory, a path graph or linear graph is a particularly simple example of a tree, namely a tree with two or more vertices that is not branched at all, that is, contains only vertices of degree 2 and 1...
, and the pathwidth of G is a number that measures how much the path was thickened to form G. More formally, a path-decomposition is
a sequence of subsets of vertices of G such that the endpoints of each edge appear in one of the subsets and such that each vertex appears in a contiguous subsequence of the subsets, and the pathwidth is one less than the size of the largest set in such a decomposition.
Pathwidth is also known as interval thickness (one less than the maximum clique size in an interval
Interval graph
In graph theory, an interval graph is the intersection graph of a multiset of intervals on the real line. It has one vertex for each interval in the set, and an edge between every pair of vertices corresponding to intervals that intersect.-Definition:...
supergraph of G), vertex separation number, or node searching number.
Pathwidth and path-decompositions are closely analogous to treewidth and tree decomposition
Tree decomposition
In graph theory, a tree decomposition is a mapping of a graph into a tree that can be used to speed up solving certain problems on the original graph...
s. They play a key role in the theory of graph minors: the families of graphs that are closed under graph minors and do not include all forest
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
s may be characterized as having bounded pathwidth, and the "vortices" appearing in the general structure theory for minor-closed graph families
Graph structure theorem
In mathematics, the graph structure theorem is a major result in the area of graph theory. The result establishes a deep and fundamental connection between the theory of graph minors and topological embeddings. The theorem is stated in the seventeenth of a series of 23 papers by Neil Robertson and...
have bounded pathwidth. Pathwidth, and graphs of bounded pathwidth, also have applications in VLSI design, graph drawing
Graph drawing
Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, and bioinformatics...
, and computational linguistics
Computational linguistics
Computational linguistics is an interdisciplinary field dealing with the statistical or rule-based modeling of natural language from a computational perspective....
.
It is NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
to find the pathwidth of arbitrary graphs, or even to approximate it accurately. However, the problem is fixed-parameter tractable: testing whether a graph has pathwidth k can be solved in an amount of time that depends linearly on the size of the graph but superexponentially on k. Additionally, for several special classes of graphs, such as trees
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
, the pathwidth may be computed in polynomial time without dependence on k.
Many problems in graph algorithms may be solved efficiently on graphs of bounded pathwidth, by using dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
on a path-decomposition of the graph. Path decomposition may also be used to measure the space complexity of dynamic programming algorithms on graphs of bounded treewidth.
Definition
In the first of their famous series of papers on graph minors, define a path-decomposition of a graph G to be a sequence of subsets Xi of vertices of G, with two properties:- For each edge of G, there exists an i such that both endpoints of the edge belong to subset Xi, and
- For every three indices i ≤ j ≤ k,
The second of these two properties is equivalent to requiring that the subsets containing any particular vertex form a contiguous subsequence of the whole sequence. In the language of the later papers in Robertson and Seymour's graph minor series, a path-decomposition is a tree decomposition
Tree decomposition
In graph theory, a tree decomposition is a mapping of a graph into a tree that can be used to speed up solving certain problems on the original graph...
(X,T) in which the underlying tree T of the decomposition is a path graph
Path graph
In the mathematical field of graph theory, a path graph or linear graph is a particularly simple example of a tree, namely a tree with two or more vertices that is not branched at all, that is, contains only vertices of degree 2 and 1...
.
The width of a path-decomposition is defined in the same way as for tree-decompositions, as maxi |Xi| − 1, and the pathwidth of G is the minimum width of any path-decomposition of G. The subtraction of one from the size of Xi in this definition makes little difference in most applications of pathwidth, but is used to make the pathwidth of a path graph
Path graph
In the mathematical field of graph theory, a path graph or linear graph is a particularly simple example of a tree, namely a tree with two or more vertices that is not branched at all, that is, contains only vertices of degree 2 and 1...
be equal to one.
Alternative characterizations
As describes, pathwidth can be characterized in many equivalent ways.Gluing sequences
A path decomposition can be described as a sequence of graphs Gi that are glued together by identifying pairs of vertices from consecutive graphs in the sequence, such that the result of performing all of these gluings is G. The graphs Gi may be taken as the induced subgraphs of the sets Xi in the first definition of path decompositions, with two vertices in successive induced subgraphs being glued together when they are induced by the same vertex in G, and in the other direction one may recover the sets Xi as the vertex sets of the graphs Gi. The width of the path decomposition is then one less than the maximum number of vertices in one of the graphs Gi.Interval thickness

Interval graph
In graph theory, an interval graph is the intersection graph of a multiset of intervals on the real line. It has one vertex for each interval in the set, and an edge between every pair of vertices corresponding to intervals that intersect.-Definition:...
that contains G as a subgraph. That is, for every path decomposition of G one can find an interval supergraph of G, and for every interval supergraph of G one can find a path decomposition of G, such that the width of the decomposition is one less than the clique number of the interval graph.
In one direction, suppose a path decomposition of G is given. Then one may represent the nodes of the decomposition as points on a line (in path order) and represent each vertex v as a closed interval having these points as endpoints. In this way, the path decomposition nodes containing v correspond to the representative points in the interval for v. The intersection graph
Intersection graph
In the mathematical area of graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph may be represented as an intersection graph, but some important special classes of graphs may be defined by the types of sets that are used to form...
of the intervals formed from the vertices of G is an interval graph that contains G as a subgraph. Its maximal cliques are given by the sets of intervals containing the representative points, and its maximum clique size is one plus the pathwidth of G.
In the other direction, if G is a subgraph of an interval graph with clique number p + 1, then G has a path decomposition of width p whose nodes are given by the maximal cliques of the interval graph. For instance, the interval graph shown with its interval representation in the figure has a path decomposition with five nodes, corresponding to its five maximal cliques ABC, ACD, CDE, CDF, and FG; the maximum clique size is three and the width of this path decomposition is two.
This equivalence between pathwidth and interval thickness is closely analogous to the equivalence between treewidth and the minimum clique number (minus one) of a chordal graph
Chordal graph
In the mathematical area of graph theory, a graph is chordal if each of its cycles of four or more nodes has a chord, which is an edge joining two nodes that are not adjacent in the cycle. An equivalent definition is that any chordless cycles have at most three nodes...
of which the given graph is a subgraph. Interval graphs are a special case of chordal graphs, and chordal graphs can be represented as intersection graphs of subtrees of a common tree generalizing the way that interval graphs are intersection graphs of subpaths of a path.
Vertex separation number
Suppose that the vertices of a graph G are linearly ordered. Then the vertex separation number of G is the smallest number s such that, for each vertex v, at most s vertices are earlier than v in the ordering but that have v or a later vertex as a neighbor.The vertex separation number of G is the minimum vertex separation number of any linear ordering of G. The vertex separation number was defined by , and is equal to the pathwidth of G.
This follows from the earlier equivalence with interval graph clique numbers: if G is a subgraph of an interval graph I, represented (as in the figure) in such a way that all interval endpoints are distinct, then the ordering of the left endpoints of the intervals of I has vertex separation number one less than the clique number of I. And in the other direction, from a linear ordering of G one may derive an interval representation in which the left endpoint of the interval for a vertex v is its position in the ordering and the right endpoint is the position of the neighbor of v that comes last in the ordering.
Node searching number
The node searching game on a graph is a form of pursuit-evasionPursuit-evasion
Pursuit-evasion is a family of problems in mathematics and computer science in which one group attempts to track down members of another group in an environment. Early work on problems of this type modeled the environment geometrically...
in which a set of searchers collaborate to track down a fugitive hiding in a graph. The searchers are placed on vertices of the graph while the fugitive may be in any edge of the graph, and the fugitive's location and moves are hidden from the searchers. In each turn, some or all of the searchers may move (arbitrarily, not necessarily along edges) from one vertex to another, and then the fugitive may move along any path in the graph that does not pass through a searcher-occupied vertex. The fugitive is caught when both endpoints of his edge are occupied by searchers. The node searching number of a graph is the minimum number of searchers needed to ensure that the fugitive can be guaranteed to be caught, no matter how he moves. As show, the node searching number of a graph equals its interval thickness. The optimal strategy for the searchers is to move the searchers so that in successive turns they form the separating sets of a linear ordering with minimal vertex separation number.
Bounds
Every n-vertex graph with pathwidth k has at most edges, and the maximalMaximal element
In mathematics, especially in order theory, a maximal element of a subset S of some partially ordered set is an element of S that is not smaller than any other element in S. The term minimal element is defined dually...
pathwidth-k graphs (graphs to which no more edges can be added without increasing the pathwidth) have exactly this many edges. A maximal pathwidth-k graph must be either a k-path or a k-caterpillar, two special kinds of k-tree. A k-tree is a chordal graph
Chordal graph
In the mathematical area of graph theory, a graph is chordal if each of its cycles of four or more nodes has a chord, which is an edge joining two nodes that are not adjacent in the cycle. An equivalent definition is that any chordless cycles have at most three nodes...
with exactly maximal cliques, each containing vertices; in a k-tree that is not itself a , each maximal clique either separates the graph into two or more components, or it contains a single leaf vertex, a vertex that belongs to only a single maximal clique. A k-path is a k-tree with at most two leaves, and a k-caterpillar is a k-tree in which the non-leaf vertices induce a k-path. In particular the maximal graphs of pathwidth one are exactly the caterpillar tree
Caterpillar tree
In graph theory, a caterpillar or caterpillar tree is a tree in which all the vertices of the caterpillar are within distance 1 of a central path....
s.
Since path-decompositions are a special case of tree-decompositions, the pathwidth of any graph is greater than or equal to its treewidth. The pathwidth is also less than or equal to the cutwidth, the minimum number of edges that crosses any cut between lower-numbered and higher-numbered vertices in an optimal linear arrangement of the vertices of a graph; this follows because the vertex separation number, the number of lower-numbered vertices with higher-numbered neighbors, can at most equal the number of cut edges. For similar reasons, the cutwidth is at most the pathwidth times the maximum degree
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
of the vertices in a given graph.
Any n-vertex forest
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
has pathwidth O(log n). For, in a forest, one can always find a constant number of vertices the removal of which leaves a forest that can be partitioned into two smaller subforests with at most 2n/3 vertices each. A linear arrangement formed by recursively partitioning each of these two subforests, placing the separating vertices between them, has logarithmic vertex searching number. The same technique, applied to a tree-decomposition of a graph, shows that, if the treewidth of an n-vertex graph G is t, then the pathwidth of G is O(t log n). Since outerplanar graph
Outerplanar graph
In graph theory, an undirected graph is an outerplanar graph if it can be drawn in the plane without crossings in such a way that all of the vertices belong to the unbounded face of the drawing. That is, no vertex is totally surrounded by edges...
s, series-parallel graph
Series-parallel graph
In graph theory, series-parallel graphs are graphs with two distinguished vertices called terminals, formed recursively by two simple composition operations. They can be used to model series and parallel electric circuits.-Definition and terminology:...
s, and Halin graph
Halin graph
In graph theory, a mathematical discipline, a Halin graph is a planar graph constructed from a plane embedding of a tree with at least four vertices and with no vertices of degree 2, by connecting all the leaves of the tree with a cycle that passes around the tree in the natural cyclic order...
s all have bounded treewidth, they all also have at most logarithmic pathwidth.
As well as its relations to treewidth, pathwidth is also related to clique-width
Clique-width
In graph theory, the clique-width of a graph G is the minimum number of labels needed to construct G by means of the following 4 operations :#Creation of a new vertex v with label i...
and cutwidth, via line graph
Line graph
In graph theory, the line graph L of undirected graph G is another graph L that represents the adjacencies between edges of G...
s; the line graph L(G) of a graph G has a vertex for each edge of G and two vertices in L(G) are adjacent when the corresponding two edges of G share an endpoint. Any family of graphs has bounded pathwidth if and only if its line graphs have bounded linear clique-width, where linear clique-width replaces the disjoint union operation from clique-width with the operation of adjoining a single new vertex. If a connected graph with three or more vertices has maximum degree three, then its cutwidth equals the vertex separation number of its line graph.
In any planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
, the pathwidth is at most proportional to the square root of the number of vertices. One way to find a path-decomposition with this width is (similarly to the logarithmic-width path-decomposition of forests described above) to use the planar separator theorem
Planar separator theorem
In graph theory, the planar separator theorem is a form of isoperimetric inequality for planar graphs, that states that any planar graph can be split into smaller pieces by removing a small number of vertices...
to find a set of O(√n) vertices the removal of which separates the graph into two subgraphs of at most 2n/3 vertices each, and concatenate recursively-constructed path decompositions for each of these two subgraphs. The same technique applies to any class of graphs for which a similar separator theorem holds. Since, like planar graphs, the graphs in any fixed minor-closed graph family have separators of size O(√n), it follows that the pathwidth of the graphs in any fixed minor-closed family is again O(√n). For some classes of planar graphs, the pathwidth of the graph and the pathwidth of its dual graph
Dual graph
In mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual...
must be within a constant factor of each other: bounds of this form are known for biconnected outerplanar graphs and for polyhedral graphs. For 2-connected planar graphs, the pathwidth of the dual graph less than the pathwidth of the line graph. It remains open whether the pathwidth of a planar graph and its dual are always within a constant factor of each other in the remaining cases.
In some classes of graphs, it has been proven that the pathwidth and treewidth are always equal to each other: this is true for cograph
Cograph
In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union...
s, permutation graph
Permutation graph
In areas of mathematics influenced by graph theory, a permutation graph is the intersection graph of a family of line segments that connect two parallel lines in the Euclidean plane...
s, the complements
Complement graph
In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
of comparability graph
Comparability graph
In graph theory, a comparability graph is an undirected graph that connects pairs of elements that are comparable to each other in a partial order...
s, and the comparability graphs of interval order
Interval order
In mathematics, especially order theory,the interval order for a collection of intervals on the real lineis the partial order corresponding to their left-to-right precedence relation—one interval, I1, being considered less than another, I2, if I1 is completely to the left of I2.More formally, a...
s.
In any cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
, or more generally any graph with maximum vertex degree three, the pathwidth is at most n/6 + o(n), where n is the number of vertices in the graph. There exist cubic graphs with pathwidth 0.082n, but it is not known how to reduce this gap between this lower bound and the n/6 upper bound.
Computing path-decompositions
It is NP-completeNP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
to determine whether the pathwidth of a given graph is at most k, when k is a variable given as part of the input. The best known worst-case time bounds for computing the pathwidth of arbitrary n-vertex graphs are of the form O(2n nc) for some constant c. Nevertheless several algorithms are known to compute path-decompositions more efficiently when the pathwidth is small, when the class of input graphs is limited, or approximately.
Fixed-parameter tractability
Pathwidth is fixed-parameter tractable: for any constant k, it is possible to test whether the pathwidth is at most k, and if so to find a path-decomposition of width k, in linear time. In general, these algorithms operate in two phases. In the first phase, the assumption that the graph has pathwidth k is used to find a path-decomposition or tree-decomposition that is not optimal, but whose width can be bounded as a function of k. In the second phase, a dynamic programmingDynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
algorithm is applied to this decomposition in order to find the optimal decomposition.
However, the time bounds for known algorithms of this type are exponential in k2, impractical except for the smallest values of k. For the case k = 2 an explicit linear-time algorithm based on a structural decomposition of pathwidth-2 graphs is given by .
Special classes of graphs
surveys the complexity of computing the pathwidth on various special classes of graphs. Determining whether the pathwidth of a graph G is at most k remains NP-complete when G is restricted to bounded-degree graphs, planar graphPlanar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
s, planar graphs of bounded degree, chordal graph
Chordal graph
In the mathematical area of graph theory, a graph is chordal if each of its cycles of four or more nodes has a chord, which is an edge joining two nodes that are not adjacent in the cycle. An equivalent definition is that any chordless cycles have at most three nodes...
s, chordal dominoes, the complements
Complement graph
In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
of comparability graph
Comparability graph
In graph theory, a comparability graph is an undirected graph that connects pairs of elements that are comparable to each other in a partial order...
s,,
and bipartite
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
distance-hereditary graph
Distance-hereditary graph
In graph-theoretic mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph...
s. It follows immediately that it is also NP-complete for the graph families that contain the bipartite distance-hereditary graphs, including the bipartite graphs, chordal bipartite graphs, distance-hereditary graphs, and circle graph
Circle graph
In graph theory, a circle graph is the intersection graph of a set of chords of a circle. That is, it is an undirected graph whose vertices can be associated with chords of a circle such that two vertices are adjacent if and only if the corresponding chords cross each other.-Algorithmic...
s.
However, the pathwidth may be computed in linear time for trees and forests, and for graphs of bounded treewidth including series-parallel graph
Series-parallel graph
In graph theory, series-parallel graphs are graphs with two distinguished vertices called terminals, formed recursively by two simple composition operations. They can be used to model series and parallel electric circuits.-Definition and terminology:...
s, outerplanar graph
Outerplanar graph
In graph theory, an undirected graph is an outerplanar graph if it can be drawn in the plane without crossings in such a way that all of the vertices belong to the unbounded face of the drawing. That is, no vertex is totally surrounded by edges...
s, and Halin graph
Halin graph
In graph theory, a mathematical discipline, a Halin graph is a planar graph constructed from a plane embedding of a tree with at least four vertices and with no vertices of degree 2, by connecting all the leaves of the tree with a cycle that passes around the tree in the natural cyclic order...
s. It may also be computed in polynomial time for split graph
Split graph
In graph theory, a branch of mathematics, a split graph is a graph in which the vertices can be partitioned into a clique and an independent set...
s, for the complements of chordal graphs, for permutation graph
Permutation graph
In areas of mathematics influenced by graph theory, a permutation graph is the intersection graph of a family of line segments that connect two parallel lines in the Euclidean plane...
s, for cograph
Cograph
In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union...
s, for circular-arc graph
Circular-arc graph
In graph theory, a circular-arc graph is the intersection graph of a set of arcs on the circle. It has one vertex for each arc in the set, and an edge between every pair of vertices corresponding to arcs that intersect....
s, for the comparability graphs of interval orders, and of course for interval graph
Interval graph
In graph theory, an interval graph is the intersection graph of a multiset of intervals on the real line. It has one vertex for each interval in the set, and an edge between every pair of vertices corresponding to intervals that intersect.-Definition:...
s themselves, since in that case the pathwidth is just one less than the maximum number of intervals covering any point in an interval representation of the graph.
Approximation algorithms
It is NP-hard to approximate the pathwidth of a graph to within an additive constant.The best known approximation ratio of a polynomial time approximation algorithm for pathwidth is O((log n)3/2).
For earlier approximation algorithms for pathwidth, see and . For approximations on restricted classes of graphs, see .
Graph minors
A minor of a graph G is another graph formed from G by contracting edges, removing edges, and removing vertices. Graph minors have a deep theory in which several important results involve pathwidth.Excluding a forest
If a family F of graphs is closed under taking minors (every minor of a member of F is also in F), then by the Robertson–Seymour theoremRobertson–Seymour theorem
In graph theory, the Robertson–Seymour theorem states that the undirected graphs, partially ordered by the graph minor relationship, form a well-quasi-ordering...
F can be characterized as the graphs that do not have any minor in X, where X is a finite set of forbidden minors. For instance, Wagner's theorem states that the planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
s are the graphs that have neither the complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
K5 nor the complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
K3,3 as minors. In many cases, the properties of F and the properties of X are closely related, and the first such result of this type was by , and relates bounded pathwidth with the existence of a forest
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
in the family of forbidden minors. Specifically, define a family F of graphs to have bounded pathwidth if there exists a constant p such that every graph in F has pathwidth at most p. Then, a minor-closed family F has bounded pathwidth if and only if the set X of forbidden minors for F includes at least one forest.
In one direction, this result is straightforward to prove: if X does not include at least one forest, then the X-minor-free graphs do not have bounded pathwidth. For, in this case, the X-minor-free graphs include must all forests, and in particular they include the perfect binary trees. But a perfect binary tree with k levels has pathwidth k − 1, so in this case the X-minor-free-graphs have unbounded pathwidth. In the other direction, if X contains an n-vertex forest, then the X-minor-free graphs have pathwidth at most n − 2.
Obstructions to bounded pathwidth
The property of having pathwidth at most p is, itself, closed under taking minors: if G has a path-decomposition with width at most p, then the same path-decomposition remains valid if any edge is removed from G, and any vertex can be removed from G and from its path-decomposition without increasing the width. Contraction of an edge, also, can be accomplished without increasing the width of the decomposition, by merging the sub-paths representing the two endpoints of the contracted edge. Therefore, the graphs of pathwidth at most p can be characterized by a set Xp of excluded minors.Although Xp necessarily includes at least one forest, it is not true that all graphs in Xp are forests: for instance, X1 consists of two graphs, a seven-vertex tree and the triangle K3. However, the set of trees in Xp may be precisely characterized: these trees are exactly the trees that can be formed from three trees in Xp − 1 by connecting a new root vertex by an edge to an arbitrarily chosen vertex in each of the three smaller trees. For instance, the seven-vertex tree in X1 is formed in this way from the two-vertex tree (a single edge) in X0. Based on this construction, the number of forbidden minors in Xp can be shown to be at least (p!)2. The complete set X2 of forbidden minors for pathwidth-2 graphs has been computed; it contains 110 different graphs.
Structure theory
The graph structure theoremGraph structure theorem
In mathematics, the graph structure theorem is a major result in the area of graph theory. The result establishes a deep and fundamental connection between the theory of graph minors and topological embeddings. The theorem is stated in the seventeenth of a series of 23 papers by Neil Robertson and...
for minor-closed graph families states that, for any such family F, the graphs in F can be decomposed into clique-sum
Clique-sum
In graph theory, a branch of mathematics, a clique-sum is a way of combining two graphs by gluing them together at a clique, analogous to the connected sum operation in topology...
s of graphs that can be embedded
Graph embedding
In topological graph theory, an embedding of a graph G on a surface Σ is a representation of G on Σ in which points of Σ are associated to vertices and simple arcs are associated to edges in such a way that:...
onto surfaces of bounded genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
, together with a bounded number of apexes and vortices for each component of the clique-sum. An apex is a vertex that may be adjacent to any other vertex in its component, while a vortex is a graph of bounded pathwidth that is glued into one of the faces of the bounded-genus embedding of a component. The cyclic ordering of the vertices around the face into which a vortex is embedded must be compatible with the path decomposition of the vortex, in the sense that breaking the cycle to form a linear ordering must lead to an ordering with bounded vertex separation number. This theory, in which pathwidth is intimately connected to arbitrary minor-closed graph families, has important algorithmic applications.
VLSI
In VLSI design, the vertex separation problem was originally studied as a way to partition circuits into smaller subsystems, with a small number of components on the boundary between the subsystems.use interval thickness to model the number of tracks needed in a one-dimensional layout of a VLSI circuit, formed by a set of modules that need to be interconnected by a system of nets. In their model, one forms a graph in which the vertices represent nets, and in which two vertices are connected by an edge if their nets both connect to the same module; that is, if the modules and nets are interpreted as forming the nodes and hyperedges of a hypergraph
Hypergraph
In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
then the graph formed from them is its line graph. An interval representation of a supergraph of this line graph, together with a coloring
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
of the supergraph, describes an arrangement of the nets along a system of horizontal tracks (one track per color) in such a way that the modules can be placed along the tracks in a linear order and connect to the appropriate nets. The fact that interval graphs are perfect graph
Perfect graph
In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph....
s implies that the number of colors needed, in an optimal arrangement of this type, is the same as the clique number of the interval completion of the net graph.
Gate matrix layout is a specific style of CMOS
CMOS
Complementary metal–oxide–semiconductor is a technology for constructing integrated circuits. CMOS technology is used in microprocessors, microcontrollers, static RAM, and other digital logic circuits...
VLSI layout for Boolean logic
Boolean logic
Boolean algebra is a logical calculus of truth values, developed by George Boole in the 1840s. It resembles the algebra of real numbers, but with the numeric operations of multiplication xy, addition x + y, and negation −x replaced by the respective logical operations of...
circuits. In gate matrix layouts, signals are propagated along "lines" (vertical line segments) while each gate of the circuit is formed by a sequence of device features that lie along a horizontal line segment. Thus, the horizontal line segment for each gate must cross the vertical segments for each of the lines that form inputs or outputs of the gate. As in the layouts of , a layout of this type that minimizes the number of vertical tracks on which the lines are to be arranged can be found by computing the pathwidth of a graph that has the lines as its vertices and pairs of lines sharing a gate as its edges. The same algorithmic approach can also be used to model folding problems in programmable logic array
Programmable logic array
A programmable logic array is a kind of programmable logic device used to implement combinational logic circuits. The PLA has a set of programmable AND gate planes, which link to a set of programmable OR gate planes, which can then be conditionally complemented to produce an output...
s.
Graph drawing
Pathwidth has several applications to graph drawingGraph drawing
Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, and bioinformatics...
:
- The minimal graphs that have a given crossing numberCrossing number (graph theory)In graph theory, the crossing number cr of a graph G is the lowest number of edge crossings of a planar drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero.The concept originated in...
have pathwidth that is bounded by a function of their crossing number. - The number of parallel lines on which the vertices of a tree can be drawn with no edge crossings (under various natural restrictions on the ways that adjacent vertices can be placed with respect to the sequence of lines) is proportional to the pathwidth of the tree.
- A k-crossing h-layer drawing of a graph G is a placement of the vertices of G onto h distinct horizontal lines, with edges routed as monotonic polygonal paths between these lines, in such a way that there are at most k crossings. The graphs with such drawings have pathwidth that is bounded by a function of h and k. Therefore, when h and k are both constant, it is possible in linear time to determine whether a graph has a k-crossing h-layer.
- A graph with n vertices and pathwidth p can be embedded into a three-dimensional grid of size in such a way that no two edges (represented as straight line segments between grid points) intersect each other. Thus, graphs of bounded pathwidth have embeddings of this type with linear volume.
Compiler design
In the compilationCompiler
A compiler is a computer program that transforms source code written in a programming language into another computer language...
of high-level programming language
High-level programming language
A high-level programming language is a programming language with strong abstraction from the details of the computer. In comparison to low-level programming languages, it may use natural language elements, be easier to use, or be from the specification of the program, making the process of...
s, pathwidth arises in the problem of reordering sequences of straight-line code (that is, code with no control flow
Control flow
In computer science, control flow refers to the order in which the individual statements, instructions, or function calls of an imperative or a declarative program are executed or evaluated....
branches or loops) in such a way that all the values computed in the code can be placed in machine registers
Register allocation
In compiler optimization, register allocation is the process of assigning a large number of target program variables onto a small number of CPU registers...
instead of having to be spilled into main memory. In this application, one represents the code to be compiled as a directed acyclic graph
Directed acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
in which the nodes represent the input values to the code and the values computed by the operations within the code. An edge from node x to node y in this DAG represents the fact that value x is one of the inputs to operation y. A topological ordering of the vertices of this DAG represents a valid reordering of the code, and the number of registers needed to evaluate the code in a given ordering is given by the vertex separation number of the ordering.
For any fixed number w of machine registers, it is possible to determine in linear time whether a piece of straight-line code can be reordered in such a way that it can be evaluated with at most w registers. For, if the vertex separation number of a topological ordering is at most w, the minimum vertex separation among all orderings can be no larger, so the undirected graph formed by ignoring the orientations of the DAG described above must have pathwith at most w. It is possible to test whether this is the case, using the known fixed-parameter-tractable algorithms for pathwidth, and if so to find a path-decomposition for the undirected graph, in linear time given the assumption that w is a constant. Once a path decomposition has been found, a topological ordering of width w (if one exists) can be found using dynamic programming, again in linear time.
Linguistics
describe an application of path-width in natural language processingNatural language processing
Natural language processing is a field of computer science and linguistics concerned with the interactions between computers and human languages; it began as a branch of artificial intelligence....
. In this application, sentences are modeled as graphs, in which the vertices represent words and the edges represent relationships between words; for instance if an adjective modifies a noun in the sentence then the graph would have an edge between those two words. Due to the limited capacity of human short-term memory, Kornai and Tuza argue that this graph must have bounded pathwidth (more specifically, they argue, pathwidth at most six), for otherwise humans would not be able to parse speech correctly.
Exponential algorithms
Many problems in graph algorithms may be solved efficiently on graphs of low pathwidth, by using dynamic programmingDynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
on a path-decomposition of the graph. For instance, if a linear ordering of the vertices of an n-vertex graph G is given, with vertex separation number w, then it is possible to find the maximum independent set of G in time On graphs of bounded pathwidth, this approach leads to fixed-parameter tractable algorithms, parametrized by the pathwidth. Such results are not frequently found in the literature because they are subsumed by similar algorithms parametrized by the treewidth; however, pathwidth arises even in treewidth-based dynamic programming algorithms in measuring the space complexity of these algorithms.
The same dynamic programming method also can be applied to graphs with unbounded pathwidth, leading to algorithms that solve unparametrized graph problems in exponential time. For instance, combining this dynamic programming approach with the fact that cubic graphs have pathwidth n/6 + o(n) shows that, in a cubic graph, the maximum independent set can be constructed in time O(2n/6 + o(n)), faster than previous known methods. A similar approach leads to improved exponential-time algorithms for the maximum cut
Maximum cut
For a graph, a maximum cut is a cut whose size is at least the size of any other cut. The problem of finding a maximum cut in a graph is known as the max-cut problem.The problem can be stated simply as follows...
and minimum dominating set problems in cubic graphs, and for several other NP-hard optimization problems.
See also
- BoxicityBoxicityIn graph theory, boxicity is a graph invariant, introduced by Fred S. Roberts in 1969.The boxicity of a graph is the minimum dimension in which a given graph can be represented as an intersection graph of axis-parallel boxes...
, a different way of measuring the complexity of an arbitrary graph in terms of interval graphs - Cycle rankCycle rankIn graph theory, the cycle rank of a directed graph is a digraph connectivity measure proposed first by Eggan and Büchi . Intuitively, this concept measures how close adigraph is to a directed acyclic graph , in the sense that a DAG has...
, a number that is bounded for a minor-closed graph family if and only if the family excludes a path - DegeneracyDegeneracy (graph theory)In graph theory, a k-degenerate graph is an undirected graph in which every subgraph has a vertex of degree at most k: that is, some vertex in the subgraph touches k or fewer of the subgraph's edges. The degeneracy of a graph is the smallest value of k for which it is k-degenerate...
, a measure of the sparsity of a graph that is at most equal to its path width - Graph bandwidthGraph bandwidthIn graph theory, the graph bandwidth problem to label the n vertices vi of a graph G with distinct integers f so that the quantity \max...
, a different NP-complete optimization problem involving linear layouts of graphs - Strahler numberStrahler numberIn mathematics, the Strahler number or Horton–Strahler number of a mathematical tree is a numerical measure of its branching complexity....
, a measure of the complexity of rooted trees defined similarly to pathwidth of unrooted trees

