Clique-width
Encyclopedia
In graph theory
, the clique-width of a graph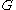
is the minimum number of labels needed to construct 
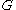by means of the following 4 operations :
Cograph
s are exactly the graphs with clique-width at most 2 ; every distance-hereditary graph
has clique-width at most 3 . Many optimization problems that are NP-hard
for more general classes of graphs may be solved efficiently by dynamic programming
on graphs of bounded clique-width . The theory of graphs of bounded clique-width resembles that for graphs of bounded treewidth, but unlike treewidth allows for dense graph
s.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the clique-width of a graph
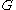is the minimum number of labels needed to construct 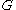by means of the following 4 operations :- Creation of a new vertex v with label i ( noted i(v) )
- Disjoint union of two labeled graphs G and H ( denoted
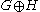) - Joining by an edge every vertex labeled i to every vertex labeled j (denoted n(i,j))
- Renaming label i to label j ( denoted p(i,j) )
Cograph
Cograph
In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union...
s are exactly the graphs with clique-width at most 2 ; every distance-hereditary graph
Distance-hereditary graph
In graph-theoretic mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph...
has clique-width at most 3 . Many optimization problems that are NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
for more general classes of graphs may be solved efficiently by dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
on graphs of bounded clique-width . The theory of graphs of bounded clique-width resembles that for graphs of bounded treewidth, but unlike treewidth allows for dense graph
Dense graph
In mathematics, a dense graph is a graph in which the number of edges is close to the maximal number of edges. The opposite, a graph with only a few edges, is a sparse graph...
s.