
Split graph
Encyclopedia
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
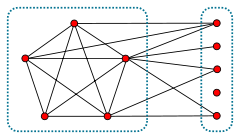
, a branch of mathematics, a split graph is a graph in which the vertices can be partitioned into a clique
Clique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
and an independent set
Independent set (graph theory)
In graph theory, an independent set or stable set is a set of vertices in a graph, no two of which are adjacent. That is, it is a set I of vertices such that for every two vertices in I, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in I...
. Split graphs were first studied by , and independently introduced by .
A split graph may have more than one partition into a clique and an independent set; for instance, the path a–b–c is a split graph, the vertices of which can be partitioned in three different ways:
- the clique {a,b} and the independent set {c}
- the clique {b,c} and the independent set {a}
- the clique {b} and the independent set {a,c}
Split graphs can be characterized in terms of their forbidden induced subgraphs: a graph is split if and only if no induced subgraph is a cycle
Cycle graph
In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
on four or five vertices, or a pair of disjoint edges (the complement of a 4-cycle).
Relation to other graph families
From the definition, split graphs are clearly closed under complementation. Another characterization of split graphs involves complementation: they are chordal graphChordal graph
In the mathematical area of graph theory, a graph is chordal if each of its cycles of four or more nodes has a chord, which is an edge joining two nodes that are not adjacent in the cycle. An equivalent definition is that any chordless cycles have at most three nodes...
s the complements of which are also chordal. Just as chordal graphs are the intersection graph
Intersection graph
In the mathematical area of graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph may be represented as an intersection graph, but some important special classes of graphs may be defined by the types of sets that are used to form...
s of subtrees of trees, split graphs are the intersection graphs of distinct substars of star graphs. Almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
chordal graphs are split graphs; that is, in the limit as n goes to infinity, the fraction of n-vertex chordal graphs that are split approaches one.
Because chordal graphs are perfect
Perfect graph
In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph....
, so are the split graphs. The double split graphs, a family of graphs derived from split graphs by doubling every vertex (so the clique comes to induce an antimatching and the independent set comes to induce a matching), figure prominently as one of five basic classes of perfect graphs from which all others can be formed in the proof by of the Strong Perfect Graph Theorem.
If a graph is both a split graph and an interval graph
Interval graph
In graph theory, an interval graph is the intersection graph of a multiset of intervals on the real line. It has one vertex for each interval in the set, and an edge between every pair of vertices corresponding to intervals that intersect.-Definition:...
, then its complement is both a split graph and a comparability graph
Comparability graph
In graph theory, a comparability graph is an undirected graph that connects pairs of elements that are comparable to each other in a partial order...
, and vice versa. The split comparability graphs, and therefore also the split interval graphs, can be characterized in terms of a set of three forbidden induced subgraphs. The split cograph
Cograph
In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union...
s are exactly the threshold graph
Threshold graph
In graph theory, a threshold graph is a graph that can be constructed from a one-vertex graph by repeated applications of the following two operations:#Addition of a single isolated vertex to the graph....
s, and the split permutation graph
Permutation graph
In areas of mathematics influenced by graph theory, a permutation graph is the intersection graph of a family of line segments that connect two parallel lines in the Euclidean plane...
s are exactly the interval graphs that have interval graph complements. Split graphs have cochromatic number
Cocoloring
In graph theory, a cocoloring of a graph G is an assignment of colors to the vertices such that each color class forms an independent set in G or in the complement of G. The cochromatic number z of G is the least number of colors needed in any cocolorings of G...
2.
Maximum clique and maximum independent set
Let G be a split graph, partitioned into a clique C and an independent set I. Then every maximal clique in a split graph is either C itself, or the neighborhood of a vertex in I. Thus, it is easy to identify the maximum clique, and complementarily the maximum independent set in a split graph. In any split graph, one of the following three possibilities must be true:- There exists a vertex x in I such that C ∪ {x} is complete. In this case, C ∪ {x} is a maximum clique and I is a maximum independent set.
- There exists a vertex x in C such that I ∪ {x} is independent. In this case, I ∪ {x} is a maximum independent set and C is a maximum clique.
- C is a maximal clique and I is a maximal independent set. In this case, G has a unique partition (C,I) into a clique and an independent set, C is the maximum clique, and I is the maximum independent set.
Some other optimization problems that are NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
on more general graph families, including graph coloring
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
, are similarly straightforward on split graphs.
Degree sequences
One remarkable property of split graphs is that they can be recognized solely from their degree sequences. Let the degree sequence of a graph G be d1 ≥ d2 ≥ ... ≥ dn, and let m be the largest value of i such that di ≥ i - 1. Then G is a split graph if and only if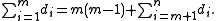
If this is the case, then the m vertices with the largest degrees form a maximum clique in G, and the remaining vertices constitute an independent set.
Counting split graphs
showed that n-vertex split graphs with n are in one-to-one correspondence with certain Sperner families. Using this fact, he determined a formula for the number of (nonisomorphic) split graphs on n vertices. For small values of n, starting from n = 1, these numbers are- 1, 2, 4, 9, 21, 56, 164, 557, 2223, 10766, 64956, 501696, ... .
This graph enumeration
Graph enumeration
In combinatorics, an area of mathematics, graph enumeration describes a class of combinatorial enumeration problems in which one must count undirected or directed graphs of certain types, typically as a function of the number of vertices of the graph...
result was also proved earlier by .
Further reading
- A chapter on split graphs appears in the book by Martin Charles GolumbicMartin Charles GolumbicMartin Charles Golumbic is a mathematician and computer scientist, best known for his work in algorithmic graph theory and in artificial intelligence. He is the founding editor-in-chief of the journal Annals of Mathematics and Artificial Intelligence.-Biography:Golumbic was born in 1948 in Erie,...
, "Algorithmic Graph Theory and Perfect Graphs".

