
Chordal graph
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
area of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
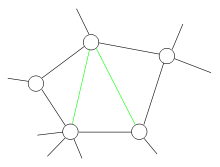
, a graph is chordal if each of its cycle
Cycle (graph theory)
In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...
s of four or more nodes has a chord, which is an edge joining two nodes that are not adjacent in the cycle. An equivalent definition is that any chordless cycles have at most three nodes. Some also state this as a chordal graph is a graph with no induced cycles of length more than three.
Chordal graphs are a subset of the perfect graph
Perfect graph
In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph....
s. They are sometimes also called rigid circuit graphs or triangulated graphs, though the latter term is also used for maximal planar graphs
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
.
Perfect elimination and efficient recognition
A perfect elimination ordering in a graph is an ordering of the vertices of the graph such that, for each vertex v, v and the neighbors of v that occur after v in the order form a cliqueClique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
. A graph is chordal if and only if it has a perfect elimination ordering .
(see also ) show that a perfect elimination ordering of a chordal graph may be found efficiently using an algorithm known as lexicographic breadth-first search
Lexicographic breadth-first search
In computer science, lexicographic breadth-first search or Lex-BFS is a linear time algorithm for ordering the vertices of a graph, that is used as part of other graph algorithms such as the recognition of chordal graphs and optimal coloring of distance-hereditary graphs...
. This algorithm maintains a partition of the vertices of the graph into a sequence of sets; initially this sequence consists of a single set with all vertices. The algorithm repeatedly chooses a vertex v from the earliest set in the sequence that contains previously-unchosen vertices, and splits each set S of the sequence into two smaller subsets, the first consisting of the neighbors of v in S and the second consisting of the non-neighbors. When this splitting process has been performed for all vertices, the sequence of sets has one vertex per set, in the reverse of a perfect elimination ordering.
Since both this lexicographic breadth first search process and the process of testing whether an ordering is a perfect elimination ordering can be performed in linear time, it is possible to recognize chordal graphs in linear time. The graph sandwich problem
Graph sandwich problem
In graph theory and computer science, the graph sandwich problem is the study of incomplete models of pairwise relations between objects from a certain collection, and how to complete them.Given a vertex set V, a mandatory edge set E1,...
on chordal graphs is NP-complete ,
whereas the probe graph problem on chordal graphs has polynomial-time
complexity .
The set of all perfect elimination orderings of a chordal graph can be modeled as the basic words of an antimatroid
Antimatroid
In mathematics, an antimatroid is a formal system that describes processes in which a set is built up by including elements one at a time, and in which an element, once available for inclusion, remains available until it is included...
; use this connection to antimatroids as part of an algorithm for efficiently listing all perfect elimination orderings of a given chordal graph.
Maximal cliques and graph coloring
Another application of perfect elimination orderings is finding a maximum cliqueClique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
of a chordal graph in polynomial-time, while the same problem for general graphs is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
. More generally, a chordal graph can have only linearly many maximal cliques, while non-chordal graphs may have exponentially many. To list all maximal cliques of a chordal graph, simply find a perfect elimination ordering, form a clique for each vertex v together with the neighbors of v that are later than v in the perfect elimination ordering, and test whether each of the resulting cliques is maximal.
The largest maximal clique is a maximum clique, and, as chordal graphs are perfect, the size of this clique equals the chromatic number of the chordal graph. Chordal graphs are perfectly orderable: an optimal coloring may be obtained by applying a greedy coloring
Greedy coloring
In the study of graph coloring problems in mathematics and computer science, a greedy coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color...
algorithm to the vertices in the reverse of a perfect elimination ordering .
Minimal separators
In any graph, a vertex separatorVertex separator
In graph theory, a vertex subset S \subset V is a vertex separator for nonadjacent vertices a and b if the removal of S from the graph separates a and b into distinct connected components.-Examples:...
is a set of vertices the removal of which leaves the remaining graph disconnected; a separator is minimal if it has no proper subset that is also a separator. According to a theorem of , the chordal graphs are exactly the graphs in which each minimal separator is a clique; Dirac used this characterization to prove that chordal graphs are perfect
Perfect graph
In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph....
.
The family of chordal graphs may be defined inductively, as the graphs whose vertices can be divided into three nonempty subsets A, S, and B, such that A ∪ S and S ∪ B both form chordal induced subgraphs, S is a clique, and there are no edges from A to B. That is, they are the graphs that have a recursive decomposition by clique separators into smaller subgraphs. For this reason, chordal graphs have also sometimes been called decomposable graphs.
Intersection graphs of subtrees

Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
and their subtrees.
From a collection of subtrees of a tree, one can define a subtree graph, which is an intersection graph
Intersection graph
In the mathematical area of graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph may be represented as an intersection graph, but some important special classes of graphs may be defined by the types of sets that are used to form...
that has one vertex per subtree and an edge connecting any two subtrees that overlap in one or more nodes of the tree. As Gavril showed, the subtree graphs are exactly the chordal graphs.
A representation of a chordal graph as an intersection of subtrees forms a tree decomposition
Tree decomposition
In graph theory, a tree decomposition is a mapping of a graph into a tree that can be used to speed up solving certain problems on the original graph...
of the graph, with treewidth equal to one less than the size of the largest clique in the graph; the tree decomposition of any graph G can be viewed in this way as a representation of G as a subgraph of a chordal graph. The tree decomposition of a graph is also the junction tree of the junction tree algorithm.
Subclasses
The interval graphInterval graph
In graph theory, an interval graph is the intersection graph of a multiset of intervals on the real line. It has one vertex for each interval in the set, and an edge between every pair of vertices corresponding to intervals that intersect.-Definition:...
s are the intersection graphs of subtrees of path graph
Path graph
In the mathematical field of graph theory, a path graph or linear graph is a particularly simple example of a tree, namely a tree with two or more vertices that is not branched at all, that is, contains only vertices of degree 2 and 1...
s, a special case of trees; therefore, they are a subfamily of the chordal graphs.
The split graph
Split graph
In graph theory, a branch of mathematics, a split graph is a graph in which the vertices can be partitioned into a clique and an independent set...
s are exactly the graphs that are both chordal and the complements of chordal graphs. showed that, in the limit as n goes to infinity, the fraction of n-vertex chordal graphs that are split approaches one.
The ptolemaic graphs, are exactly the graphs that are both chordal and distance-hereditary
Distance-hereditary graph
In graph-theoretic mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph...
.
The quasi-threshold graph
Quasi-threshold graph
In graph theory, a trivially perfect graph is a graph with the property that in each of its induced subgraphs the size of the maximum independent set equals the number of maximal cliques...
s are a subclass of the ptolemaic graphs that are exactly the graphs that are both chordal and cograph
Cograph
In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union...
s.
The block graph
Block graph
In graph theory, a branch of combinatorial mathematics, a block graph is a type of undirected graph in which every biconnected component is a clique...
s are another subclass of ptolemaic graphs in which every two maximal cliques have at most one vertex in common. In a special case of the block graphs, the windmill graph
Windmill graph
In the mathematical field of graph theory, the windmill graph Wd is a simple undirected graph with n+1 vertices and nk/2 edges. It is defined for k ≥ 2 and n ≥ 2....
s, the common vertex is the same for every pair of cliques.
The strongly chordal graph
Strongly chordal graph
In the mathematical area of graph theory, an undirected graph G is strongly chordal if it is a chordal graph and every cycle of even length in G has an odd chord, i.e., an edge that connects two vertices that are an odd distance apart from each other in the cycle.-Characterizations:Strongly...
s are graphs that are chordal and contain no n-sun (n>=3) as induced subgraph.
The k-trees
K-tree
In graph theory, a k-tree is a chordal graph all of whose maximal cliques are the same size k + 1 and all of whose minimal clique separators are also all the same size k....
are the chordal graphs in which all maximal cliques and all maximal clique separators have the same size. The Apollonian network
Apollonian network
In combinatorial mathematics, an Apollonian network is an undirected graph formed by a process of recursively subdividing a triangle into three smaller triangles. Apollonian networks may equivalently be defined as the planar 3-trees, the maximal planar chordal graphs, the uniquely 4-colorable...
s are the chordal maximal planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
s, or equivalently the planar 3-trees. The maximal outerplanar graph
Outerplanar graph
In graph theory, an undirected graph is an outerplanar graph if it can be drawn in the plane without crossings in such a way that all of the vertices belong to the unbounded face of the drawing. That is, no vertex is totally surrounded by edges...
s are a subclass of 2-trees, and therefore are also chordal.
Superclasses
The chordal graphs are a subclass of the well known perfect graphPerfect graph
In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph....
s.
Other superclasses of chordal graphs include the weakly chordal graphs, the odd-hole-free graphs, and the even-hole-free graph
Even-hole-free graph
In the mathematical area of graph theory, a graph is even-hole-free if it contains no induced cycle with an even number of vertices. demonstrated that every even-hole-free graph contains a bisimplicial vertex, which settled a conjecture by Reed.-Recognition:...
s. In fact, chordal graphs
are precisely the graphs that are both odd-hole-free and even-hole-free (see holes
in graph theory).

