In graph theory

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

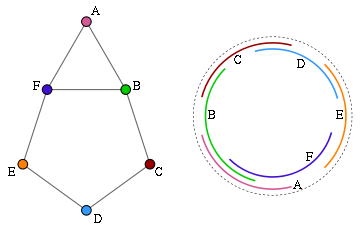
, a circular-arc graph is the intersection graph

Intersection graph

In the mathematical area of graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph may be represented as an intersection graph, but some important special classes of graphs may be defined by the types of sets that are used to form...

 of a set of arcs

Arc (geometry)

In geometry, an arc is a closed segment of a differentiable curve in the two-dimensional plane; for example, a circular arc is a segment of the circumference of a circle...

 on the circle. It has one vertex

Vertex (graph theory)

In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...

 for each arc in the set, and an edge between every pair of vertices corresponding to arcs that intersect.

Formally, let
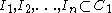
be a set of arcs. Then the corresponding circular-arc graph is G = (V, E) where
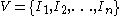
and

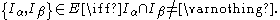
A family of arcs that corresponds to G is called an arc model.

Recognition

demonstrated the first polynomial recognition algorithm for circular-arc graphs, which runs in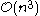 time. More recently, gave the first linear 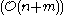time recognition algorithm.

Relation to other graph classes

Circular-arc graphs are a natural generalization of interval graph

Interval graph

In graph theory, an interval graph is the intersection graph of a multiset of intervals on the real line. It has one vertex for each interval in the set, and an edge between every pair of vertices corresponding to intervals that intersect.-Definition:...

s. If a circular-arc graph G has an arc model that leaves some point of the circle uncovered, the circle can be cut at that point and stretched to a line, which results in an interval representation. Unlike interval graphs, however, circular-arc graphs are not always perfect

Perfect graph

In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph....

, as the odd chordless cycles C₅, C₇, etc., are circular-arc graphs.

Unit circular-arc graphs

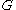is a unit circular-arc graph if there exists a corresponding arc model such that each arc is of equal length.

Proper circular-arc graphs

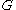is a proper circular-arc graph (also known as a circular interval graph ) if there exists a corresponding arc model such that no arc properly contains another. Recognizing these graphs and constructing a proper arc model can both be performed in linear 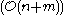time.

Helly circular-arc graphs

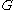is a Helly circular-arc graph if there exists a corresponding arc model such that the arcs constitute a Helly family

Helly family

In combinatorics, a Helly family of order k is a family of sets such that any minimal subfamily with an empty intersection has k or fewer sets in it. In other words, any subfamily such that every k-fold intersection is non-empty has non-empty total intersection.The k-Helly property is the property...

. gives a characterization of this class that implies an 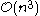recognition algorithm.

give other characterizations (including one by forbidden induced subgraphs) of this class, which imply a recognition algorithm that runs in O(n+m) time when the input is a graph. If the input graph is not a Helly circular-arc graph, then the algorithm returns a certificate of this fact in the form of a forbidden induced subgraph. They also gave an O(n) time algorithm for determining whether a given circular-arc model has the Helly property.

Applications

Circular-arc graphs are useful in modeling periodic resource allocation

Resource allocation

Resource allocation is used to assign the available resources in an economic way. It is part of resource management. In project management, resource allocation is the scheduling of activities and the resources required by those activities while taking into consideration both the resource...

 problems in operations research

Operations research

Operations research is an interdisciplinary mathematical science that focuses on the effective use of technology by organizations...

. Each interval represents a request for a resource for a specific period repeated in time.