
Graph bandwidth
Encyclopedia
In graph theory
, the graph bandwidth problem to label the n vertices vi of a graph G with distinct integers f(vi) so that the quantity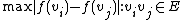 is minimized (E is the edge set of G).
is minimized (E is the edge set of G).
The problem may be visualized as placing the vertices of a graph at distinct integer points along the x-axis so that the length of the longest edge is minimized. Such placement is called linear graph arrangement, linear graph layout or linear graph placement.
The weighted graph bandwidth problem is a generalization wherein the edges are assigned weights wij and the cost function to be minimized is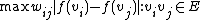 .
.
In terms of matrices, the (unweighted) graph bandwidth is the bandwidth of the symmetric matrix which is the adjacency matrix
of the graph.
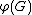 is given by an explicit formula.
is given by an explicit formula.
The bandwidth of a path graph
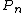 on n vertices is
on n vertices is 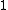 , and for a complete graph
, and for a complete graph 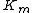 we have
we have 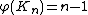 . For the complete bipartite graph
. For the complete bipartite graph
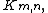
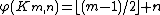 , assuming
, assuming 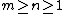 ,
,
which was proved by Chvátal. As a special case of this formula, the star graph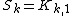 on k+1 vertices has bandwidth
on k+1 vertices has bandwidth 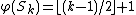 .
.
For the hypercube graph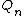 on
on 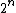 vertices the bandwidth was determined by to be
vertices the bandwidth was determined by to be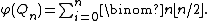
Chvatálová showed that the bandwidth of the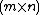 square grid graph
square grid graph
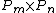 , that is, the Cartesian product
, that is, the Cartesian product
of two path graphs on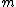 and
and  vertices, is equal to
vertices, is equal to 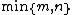 .
.
letting diam(G) denote the diameter of G, the following inequalities hold: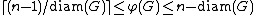
As noted in the previous section, the star graph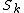 , a structurally
, a structurally
very simple example of a tree
, has comparatively large bandwidth. On the other hand,
proved that if T is a tree of maximum degree at most ∆, then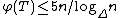 .
.
More generally, for planar graph
s of bounded maximum degree at most ∆, a similar bound holds (cf. ):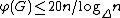 .
.
.
The bandwidth problem is NP-hard
, even for some special cases. Regarding the existence of efficient
approximation algorithm
s, it is known that the bandwidth is NP-hard to approximate
within any constant, and this even holds when the input graphs are restricted to caterpillar tree
s . On the other hand, a number of polynomially-solvable special cases are known. A heuristic
algorithm for obtaining linear graph layouts of low bandwidth is the Cuthill–McKee algorithm.
One area is sparse matrix
/band matrix
handling, and general algorithms from this area, such as Cuthill–McKee algorithm, may be applied to find approximate solutions for the graph bandwidth problem.
Another application domain is in electronic design automation
. In standard cell
design methodology. Typically standard cells have the same height, and their placement
is arranged in a number of rows. In this context, graph bandwidth problem models the problem of placement of a set of standard cells in a singe row with the goal of minimizing the maximal propagation delay
(which is assumed to be proportional to wire length).
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the graph bandwidth problem to label the n vertices vi of a graph G with distinct integers f(vi) so that the quantity
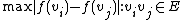 is minimized (E is the edge set of G).
is minimized (E is the edge set of G).The problem may be visualized as placing the vertices of a graph at distinct integer points along the x-axis so that the length of the longest edge is minimized. Such placement is called linear graph arrangement, linear graph layout or linear graph placement.
The weighted graph bandwidth problem is a generalization wherein the edges are assigned weights wij and the cost function to be minimized is
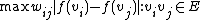 .
.In terms of matrices, the (unweighted) graph bandwidth is the bandwidth of the symmetric matrix which is the adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
of the graph.
Bandwidth formulas for some graphs
For several families of graphs , the bandwidth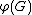 is given by an explicit formula.
is given by an explicit formula.The bandwidth of a path graph
Path graph
In the mathematical field of graph theory, a path graph or linear graph is a particularly simple example of a tree, namely a tree with two or more vertices that is not branched at all, that is, contains only vertices of degree 2 and 1...
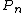 on n vertices is
on n vertices is  , and for a complete graph
, and for a complete graph 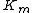 we have
we have 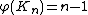 . For the complete bipartite graph
. For the complete bipartite graphComplete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
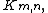
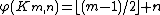 , assuming
, assuming 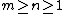 ,
,which was proved by Chvátal. As a special case of this formula, the star graph
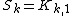 on k+1 vertices has bandwidth
on k+1 vertices has bandwidth 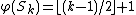 .
.For the hypercube graph
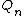 on
on 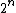 vertices the bandwidth was determined by to be
vertices the bandwidth was determined by to be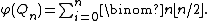
Chvatálová showed that the bandwidth of the
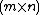 square grid graph
square grid graphLattice graph
The terms lattice graph, mesh graph, or grid graph refer to a number of categories of graphs whose drawing corresponds to some grid/mesh/lattice, i.e., its vertices correspond to the nodes of the mesh and its edges correspond to the ties between the nodes.-Square grid graph:A common type of a...
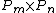 , that is, the Cartesian product
, that is, the Cartesian productCartesian product of graphs
In graph theory, the Cartesian product G \square H of graphs G and H is a graph such that* the vertex set of G \square H is the Cartesian product V × V; and...
of two path graphs on
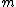 and
and  vertices, is equal to
vertices, is equal to 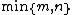 .
.Bounds
The bandwidth of a graph can be bounded in terms of various other graph parameters. For instance, letting χ(G) denote the chromatic number of G,- φ(G) ≥ χ(G)-1;
letting diam(G) denote the diameter of G, the following inequalities hold:
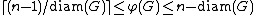
As noted in the previous section, the star graph
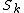 , a structurally
, a structurallyvery simple example of a tree
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
, has comparatively large bandwidth. On the other hand,
proved that if T is a tree of maximum degree at most ∆, then
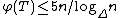 .
.More generally, for planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
s of bounded maximum degree at most ∆, a similar bound holds (cf. ):
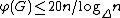 .
.Computing the bandwidth
Both the unweighted and weighted versions are special cases of the quadratic bottleneck assignment problemQuadratic bottleneck assignment problem
In mathematics, the quadratic bottleneck assignment problem is one of fundamental combinatorial optimization problems in the branch of optimization or operations research, from the category of the facilities location problems....
.
The bandwidth problem is NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
, even for some special cases. Regarding the existence of efficient
approximation algorithm
Approximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
s, it is known that the bandwidth is NP-hard to approximate
Hardness of approximation
In computer science, hardness of approximation is a field that studies the algorithmic complexity of finding near-optimal solutions to optimization problems. It complements the study of approximation algorithms by proving, for certain problems, a limit on the factors with which their solution can...
within any constant, and this even holds when the input graphs are restricted to caterpillar tree
Caterpillar tree
In graph theory, a caterpillar or caterpillar tree is a tree in which all the vertices of the caterpillar are within distance 1 of a central path....
s . On the other hand, a number of polynomially-solvable special cases are known. A heuristic
Heuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
algorithm for obtaining linear graph layouts of low bandwidth is the Cuthill–McKee algorithm.
Applications
The interest in this problem comes from some application areas.One area is sparse matrix
Sparse matrix
In the subfield of numerical analysis, a sparse matrix is a matrix populated primarily with zeros . The term itself was coined by Harry M. Markowitz....
/band matrix
Band matrix
In mathematics, particularly matrix theory, a band matrix is a sparse matrix whose non-zero entries are confined to a diagonal band, comprising the main diagonal and zero or more diagonals on either side.-Matrix bandwidth:...
handling, and general algorithms from this area, such as Cuthill–McKee algorithm, may be applied to find approximate solutions for the graph bandwidth problem.
Another application domain is in electronic design automation
Electronic design automation
Electronic design automation is a category of software tools for designing electronic systems such as printed circuit boards and integrated circuits...
. In standard cell
Standard cell
In semiconductor design, standard cell methodology is a method of designing application-specific integrated circuits with mostly digital-logic features. Standard cell methodology is an example of design abstraction, whereby a low-level very-large-scale integration layout is encapsulated into an...
design methodology. Typically standard cells have the same height, and their placement
Placement (EDA)
Placement is an essential step in electronic design automation - the portion of the physical design flow that assigns exact locations for various circuitcomponents within the chip’s core area...
is arranged in a number of rows. In this context, graph bandwidth problem models the problem of placement of a set of standard cells in a singe row with the goal of minimizing the maximal propagation delay
Propagation delay
Propagation delay is a technical term that can have a different meaning depending on the context. It can relate to networking, electronics or physics...
(which is assumed to be proportional to wire length).
See also
- Pathwidth, a different NP-complete optimization problem involving linear layouts of graphs.
External links
- Minimum bandwidth problem, in: Pierluigi Crescenzi and Viggo Kann (eds.), A compendium of NP optimization problems. Accessed May 26, 2010.

