In graph theory

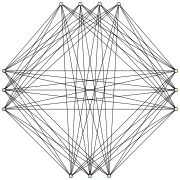
Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, a cograph, or complement-reducible graph, or P₄-free graph, is a graph

Graph (mathematics)

In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...

 that can be generated from the single-vertex graph K₁ by complementation

Complement graph

In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...

 and disjoint union

Graph operations

Operations on graphs produce new graphs from old ones. They may be separated into the following major categories.-Elementary operations:These are sometimes called "editing operations" on graphs...

. That is, the family of cographs is the smallest class of graphs that includes K₁ and is closed under complementation and disjoint union.

Cographs have been discovered independently by several authors since the 1970s; early references include , , , and . They have also been called D*-graphs , hereditary Dacey graphs , and 2-parity graphs .

See, e.g., for more detailed coverage of cographs, including the facts presented here.

Definition and characterization

Any cograph may be constructed using the following rules:

1. any single vertex graph is a cograph;
2. if 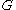is a cograph, so is its complement ;
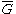3. if 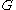and 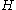are cographs, so is their disjoint union .

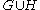Several alternative characterizations of cographs can be given. Among them:

• A cograph is a graph which does not contain the path
  Path (graph theory)
  In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
  
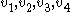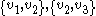   P₄ on 4 vertices (and hence of length 3) as an induced subgraph. That is, a graph is a cograph if and only if for any four vertices , if and 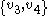are edges of the graph then at least one of 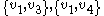or 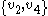is also an edge .
• A cograph is a graph all of whose induced subgraphs have the property that any maximal clique
  Clique (graph theory)
  In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
  
   intersects any maximal independent set
  Maximal independent set
  In graph theory, a maximal independent set or maximal stable set is an independent set that is not a subset of any other independent set. That is, it is a set S such that every edge of the graph has at least one endpoint not in S and every vertex not in S has at least one neighbor in S...
  
   in a single vertex.
• A cograph is a graph in which every nontrivial induced subgraph has at least two vertices with the same neighbourhoods.
• A cograph is a graph in which every connected induced subgraph has a disconnected complement.
• A cograph is a graph all of whose connected induced subgraphs have diameter
  Distance (graph theory)
  In the mathematical field of graph theory, the distance between two vertices in a graph is the number of edges in a shortest path connecting them. This is also known as the geodesic distance...
  
   at most 2.
• A cograph is a graph in which every connected component
  Connected component (graph theory)
  In graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices. For example, the graph shown in the illustration on the right has three connected components...
  
   is a distance-hereditary graph
  Distance-hereditary graph
  In graph-theoretic mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph...
  
   with diameter at most 2.
• A cograph is a graph with clique-width
  Clique-width
  In graph theory, the clique-width of a graph G is the minimum number of labels needed to construct G by means of the following 4 operations :#Creation of a new vertex v with label i...
  
   at most 2 .

All complete graph

Complete graph

In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...

s, complete bipartite graph

Complete bipartite graph

In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...

s, threshold graph

Threshold graph

In graph theory, a threshold graph is a graph that can be constructed from a one-vertex graph by repeated applications of the following two operations:#Addition of a single isolated vertex to the graph....

s, and Turán graph

Turán graph

The Turán graph T is a graph formed by partitioning a set of n vertices into r subsets, with sizes as equal as possible, and connecting two vertices by an edge whenever they belong to different subsets. The graph will have subsets of size \lceil n/r\rceil, and r- subsets of size \lfloor n/r\rfloor...

s are cographs. Every cograph is distance-hereditary, a comparability graph

Comparability graph

In graph theory, a comparability graph is an undirected graph that connects pairs of elements that are comparable to each other in a partial order...

, and perfect

Perfect graph

In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph....

.

Cographs are the comparability graph

Comparability graph

In graph theory, a comparability graph is an undirected graph that connects pairs of elements that are comparable to each other in a partial order...

s of series-parallel partial order

Series-parallel partial order

In order-theoretic mathematics, a series-parallel partial order is a partially ordered set built up from smaller series-parallel partial orders by two simple composition operations....

s .

Cotrees

A cotree is a tree in which the internal nodes are labeled with the numbers 0 and 1. Every cotree T defines a cograph G having the leaves of T as vertices, and in which the subtree rooted at each node of T corresponds to the induced subgraph in G defined by the set of leaves descending from that node:

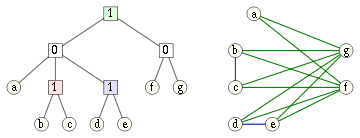
• A subtree consisting of a single leaf node corresponds to an induced subgraph with a single vertex.
• A subtree rooted at a node labeled 0 corresponds to the union of the subgraphs defined by the children of that node.
• A subtree rooted at a node labeled 1 corresponds to the join of the subgraphs defined by the children of that node; that is, we form the union and add an edge between every two vertices corresponding to leaves in different subtrees. Alternatively, the join of a set of graphs can be viewed as formed by complementing each graph, forming the union of the complements, and then complementing the resulting union.

An equivalent way of describing the cograph formed from a cotree is that two vertices are connected by an edge if and only if the lowest common ancestor

Lowest common ancestor

The lowest common ancestor is a concept in graph theory and computer science. Let T be a rooted tree with n nodes. The lowest common ancestor is defined between two nodes v and w as the lowest node in T that has both v and w as descendants .The LCA of v and w in T is the shared ancestor of v...

 of the corresponding leaves is labeled by 1. Conversely, every cograph can be represented in this way by a cotree. If we require the labels on any root-leaf path of this tree to alternate between 0 and 1, this representation is unique .

Computational properties

Cographs may be recognized in linear time, and a cotree representation constructed, using modular decomposition

Modular decomposition

In graph theory, the modular decomposition is a decomposition of an undirected graph into subsets of vertices called modules. A module is a generalization of a connected component of a graph. Unlike connected components, however, one module can be a proper subset of another...

 , partition refinement

Partition refinement

In the design of algorithms, partition refinement is a technique for representing a partition of a set as a data structure that allows the partition to be refined by splitting its sets into a larger number of smaller sets. In that sense it is dual to the union-find data structure, which also...

 , or split decomposition . Once a cotree representation has been constructed, many familiar graph problems may be solved via simple bottom-up calculations on the cotrees.

For instance, to find the maximum clique

Clique problem

In computer science, the clique problem refers to any of the problems related to finding particular complete subgraphs in a graph, i.e., sets of elements where each pair of elements is connected....

 in a cograph, compute in bottom-up order the maximum clique in each subgraph represented by a subtree of the cotree. For a node labeled 0, the maximum clique is the maximum among the cliques computed for that node's children. For a node labeled 1, the maximum clique is the union of the cliques computed for that node's children, and has size equal to the sum of the children's clique sizes. Thus, by alternately maximizing and summing values stored at each node of the cotree, we may compute the maximum clique size, and by alternately maximizing and taking unions, we may construct the maximum clique itself. Similar bottom-up tree computations allow the maximum independent set

Maximal independent set

In graph theory, a maximal independent set or maximal stable set is an independent set that is not a subset of any other independent set. That is, it is a set S such that every edge of the graph has at least one endpoint not in S and every vertex not in S has at least one neighbor in S...

, vertex coloring number

Graph coloring

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...

, maximum clique cover, and Hamiltonicity (that is the existence of a Hamiltonian cycle

Hamiltonian path problem

In the mathematical field of graph theory the Hamiltonian path problem and the Hamiltonian cycle problem are problems of determining whether a Hamiltonian path or a Hamiltonian cycle exists in a given graph . Both problems are NP-complete...

) to be computed in linear time from a cotree representation of a cograph. One can also use cotrees to determine in linear time whether two cographs are isomorphic

Graph isomorphism

In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...

.