Tree decomposition - AbsoluteAstronomy.com

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, a tree decomposition is a mapping of a graph

Graph (mathematics)

In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...

into a tree

Tree (graph theory)

In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...

that can be used to speed up solving certain problems on the original graph. The treewidth measures the number of graph vertices mapped onto any tree node in an optimal tree decomposition.
While it is NP-hard

NP-hard

NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...

to determine the treewidth of a graph, many NP-hard

NP-hard

combinatorial problems on graphs are solvable in polynomial time when restricted to graphs of bounded treewidth.

In machine learning

Machine learning

Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...

, tree decompositions are also called junction trees, clique trees, or join trees; they
play an important role in problems like probabilistic inference

Belief propagation

Belief propagation is a message passing algorithm for performing inference on graphical models, such as Bayesian networks and Markov random fields. It calculates the marginal distribution for each unobserved node, conditional on any observed nodes...

, constraint satisfaction

Constraint satisfaction

In artificial intelligence and operations research, constraint satisfaction is the process of finding a solution to a set of constraints that impose conditions that the variables must satisfy. A solution is therefore a vector of variables that satisfies all constraints.The techniques used in...

, query optimization

Query optimization

Query optimization is a function of many relational database management systems in which multiple query plans for satisfying a query are examined and a good query plan is identified. This may or not be the absolute best strategy because there are many ways of doing plans. There is a trade-off...

, and matrix decomposition

Matrix decomposition

In the mathematical discipline of linear algebra, a matrix decomposition is a factorization of a matrix into some canonical form. There are many different matrix decompositions; each finds use among a particular class of problems.- Example :...

.

The concept of tree decompositions and treewidth was introduced by and has since been studied by many other authors.

Definition

Intuitively, a tree decomposition represents the vertices of the given graph as subtrees of a tree, in such a way that vertices are adjacent only when the corresponding subtrees intersect. Thus, the graph forms a subgraph of the intersection graph

Intersection graph

In the mathematical area of graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph may be represented as an intersection graph, but some important special classes of graphs may be defined by the types of sets that are used to form...

of the subtrees. The full intersection graph is a chordal graph

Chordal graph

In the mathematical area of graph theory, a graph is chordal if each of its cycles of four or more nodes has a chord, which is an edge joining two nodes that are not adjacent in the cycle. An equivalent definition is that any chordless cycles have at most three nodes...

.

Each subtree associates a graph vertex with a set of tree nodes. To define this formally, we represent each tree node as the set of vertices associated with it.
Thus, given a graph G = (V, E), a tree decomposition is a pair (X, T), where X = {X₁, ..., X_n} is a family of subsets of V, and T is a tree whose nodes are the subsets X_i, satisfying the following properties:

The union of all sets X_i equals V. That is, each graph vertex is associated with at least one tree node.
For every edge (v, w) in the graph, there is a subset X_i that contains both v and w. That is, vertices are adjacent in the graph only when the corresponding subtrees have a node in common.
If X_i and X_j both contain a vertex v, then all nodes X_k of the tree in the (unique) path between X_i and X_j contain v as well. That is, the nodes associated with vertex v form a connected subset of T. This is also known as coherence, or the running intersection property. It can be stated equivalently that if , and are nodes, and is on the path from to , then .

The tree decomposition of a graph is far from unique; for example, a trivial tree decomposition contains all vertices of the graph in its single root node.

Treewidth

The width of a tree decomposition is the size of its largest set X_i minus one. The treewidth tw(G) of a graph G is the minimum width among all possible tree decompositions of G. In this definition, the size of the largest set is diminished by one in order to make the treewidth of a tree equal to one. Equivalently, the treewidth of G is one less than the size of the largest clique

Clique (graph theory)

In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...

in the chordal graph

Chordal graph

containing G with the smallest clique number. The graphs with treewidth at most k are also called partial k-trees.

It is NP-complete to determine whether a given graph G has treewidth at most a given variable k.
However, when k is any fixed constant, the graphs with treewidth k can be recognized, and a width k tree decomposition constructed for them, in linear time. The time dependence of this algorithm on k is exponential.

Treewidth may also be characterized in terms of havens

Haven (graph theory)

In graph theory, a haven is a way of describing a strategy for an evader to win a certain type of pursuit-evasion game on an undirected graph. Havens were first introduced by ; they may also be used to characterize the treewidth of graphs and to prove the existence of small separators on...

, functions describing an evasion strategy for a certain pursuit-evasion

Pursuit-evasion

Pursuit-evasion is a family of problems in mathematics and computer science in which one group attempts to track down members of another group in an environment. Early work on problems of this type modeled the environment geometrically...

game defined on a graph. A graph G has treewidth k if and only if it has a haven of order but of no higher order, where a haven of order is a function β that maps each set X of at most k vertices in G into one of the connected components of and that obeys the monotonicity property that whenever

Graph minors

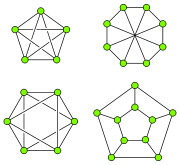
For any fixed constant k, the partial k-trees are closed under the operation of graph minors, and therefore, by the Robertson–Seymour theorem

Robertson–Seymour theorem

In graph theory, the Robertson–Seymour theorem states that the undirected graphs, partially ordered by the graph minor relationship, form a well-quasi-ordering...

, this family can be characterized in terms of a finite set of forbidden minors. For partial 1-trees (that is, forests), the single forbidden minor is a triangle, and for the partial 2-trees the single forbidden minor is the complete graph

Complete graph

In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...

on four vertices. However, the number of forbidden minors increases for larger values of k: for partial 3-trees there are four forbidden minors, the complete graph on five vertices, the octahedral graph

Octahedron

In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....

with six vertices, the eight-vertex Wagner graph

Wagner graph

In the mathematical field of graph theory, the Wagner graph is a 3-regular graph with 8 vertices and 12 edges. It is the 8-vertex Möbius ladder graph.-Properties:...

, and the pentagonal prism

Pentagonal prism

In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :...

with ten vertices.

The planar graph

Planar graph

In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...

s do not have bounded treewidth, because the n × n grid graph is a planar graph with treewidth n. Therefore, if F is a minor-closed graph family with bounded treewidth, it cannot include all planar graphs. Conversely, if some planar graph cannot occur as a minor for graphs in family F, then there is a constant k such that all graphs in F have treewidth at most k. That is, the following three conditions are equivalent to each other:

F is a minor-closed family of bounded-treewidth graphs;
One of the finitely many forbidden minors characterizing F is planar;
F is a minor-closed graph family that does not include all planar graphs.

Families of graphs with bounded treewidth include the cactus graph

Cactus graph

In graph theory, a cactus is a connected graph in which any two simple cycles have at most one vertex in common. Equivalently, every edge in such a graph belongs to at most one simple cycle. Equivalently, every block is an edge or a cycle.-Properties:Cacti are outerplanar graphs...

s, pseudoforest

Pseudoforest

In graph theory, a pseudoforest is an undirected graph in which every connected component has at most one cycle. That is, it is a system of vertices and edges connecting pairs of vertices, such that no two cycles of consecutive edges share any vertex with each other, nor can any two cycles be...

s, series-parallel graph

Series-parallel graph

In graph theory, series-parallel graphs are graphs with two distinguished vertices called terminals, formed recursively by two simple composition operations. They can be used to model series and parallel electric circuits.-Definition and terminology:...

s, outerplanar graph

Outerplanar graph

In graph theory, an undirected graph is an outerplanar graph if it can be drawn in the plane without crossings in such a way that all of the vertices belong to the unbounded face of the drawing. That is, no vertex is totally surrounded by edges...

s, and Halin graph

Halin graph

In graph theory, a mathematical discipline, a Halin graph is a planar graph constructed from a plane embedding of a tree with at least four vertices and with no vertices of degree 2, by connecting all the leaves of the tree with a cycle that passes around the tree in the natural cyclic order...

s. The control flow graph

Control flow graph

A control flow graph in computer science is a representation, using graph notation, of all paths that might be traversed through a program during its execution.- Overview :...

s arising in the compilation

Compiler

A compiler is a computer program that transforms source code written in a programming language into another computer language...

of structured programs

Structured programming

Structured programming is a programming paradigm aimed on improving the clarity, quality, and development time of a computer program by making extensive use of subroutines, block structures and for and while loops - in contrast to using simple tests and jumps such as the goto statement which could...

also have bounded treewidth, which allows certain tasks such as register allocation

In compiler optimization, register allocation is the process of assigning a large number of target program variables onto a small number of CPU registers...

to be performed efficiently on them.

Dynamic programming

At the beginning of the 1970s, it was observed that a large class of combinatorial optimization problems defined on graphs could be efficiently solved by non serial dynamic programming

Dynamic programming

In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...

as long as the graph had a bounded dimension, a parameter related to treewidth. Later, several authors independently observed at the end of the 1980s that many algorithmic problems that are NP-complete for arbitrary graphs may be solved efficiently by dynamic programming

Dynamic programming

for graphs of bounded treewidth, using the tree-decompositions of these graphs.

As an example, consider the problem of finding the maximum independent set in a graph of treewidth k. To solve this problem, first choose one of the nodes of the tree decomposition to be the root, arbitrarily. For a node X_i of the tree decomposition, let D_i be the union of the sets X_j descending from X_i. Let A(S,i), for an independent set S ⊂ X_i, denote the size of the largest independent subset I of D_i such that I ∩ X_i = S. Similarly, for an adjacent pair of nodes X_i and X_j, with X_i farther from the root of the tree than X_j, and an independent set S ⊂ X_i ∩ X_j, let B(S,i,j) denote the size of the largest independent subset I of D_i such that I ∩ X_i ∩ X_j = S. We may calculate these A and B values by a bottom-up traversal of the tree:

where the sum in the calculation of

is over the children of node

.

At each node or edge, there are at most 2^k sets S for which we need to calculate these values, so if k is a constant then the whole calculation takes constant time per edge or node. The size of the maximum independent set is the largest value stored at the root node, and the maximum independent set itself can be found (as is standard in dynamic programming algorithms) by backtracking through these stored values starting from this largest value. Thus, in graphs of bounded treewidth, the maximum independent set problem may be solved in linear time. Similar algorithms apply to many other graph problems.

This dynamic programming approach is used in machine learning

Machine learning

via the junction tree algorithm for belief propagation

Belief propagation

in graphs of bounded treewidth. It also plays a key role in algorithms for computing the treewidth and constructing tree decompositions: typically, such algorithms have a first step that approximates

Approximation algorithm

In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...

the treewidth, constructing a tree decomposition with this approximate width, and then a second step that performs dynamic programming in the approximate tree decomposition to compute the exact value of the treewidth.

Treewidth of cliques

In any tree decomposition

of a graph containing a clique

Clique (graph theory)

there is a node i in T such that

contains all the nodes of the clique. This is shown by induction

Mathematical induction

Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...

on the size of the clique. The base cases are cliques of size 1 and 2, which follow from the conditions 1 and 2 on a tree decomposition. The inductive case is a graph containing a clique of size k+1, where k is 2 or greater. Let C be the set of nodes in the clique. Since

, there are at least three nodes in the clique, call them x, y and z. We know from the induction hypothesis that there are nodes a, b and c in the tree decomposition with

.
In a tree

Tree (graph theory)

there is exactly one path between any two nodes. A second property of trees is that the three paths between a, b and c have a non-empty intersection. Let v be a node in this intersection. From condition 3 on a tree decomposition we get that

This implies that

.

It follows from this that the treewidth of a k-clique is k-1.

Treewidth of trees

A connected graph with at least two vertices has treewidth 1 if and only if it is a tree. This can be shown in two steps, first that a tree has treewidth 1, second, that a connected graph with treewidth 1 is a tree.

To show the former, use induction

Mathematical induction

Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...

on the number of vertices in the tree to show that it has a tree decomposition with no bag with size larger than two. The base case is a tree with two vertices, in which case the tree decomposition with one single node is sufficient. The inductive case is a tree

with

vertices, where

is any integer greater than

. If we remove a leaf

Leaf

A leaf is an organ of a vascular plant, as defined in botanical terms, and in particular in plant morphology. Foliage is a mass noun that refers to leaves as a feature of plants....

from the graph, we get a tree of size

. From the induction hypothesis we can create a tree decomposition

of width 1 of this graph. Let

be the unique neighbour of

and

some node in

such that

is in

. Let

added a node

with

as its only neighbour and let

with the addition that

. Now

is a tree decomposition of

with width 1.

Now it remains to show that a connected graph with treewidth 1 is a tree. The contrapositive statement is that a graph with a cycle does not have treewidth 1. A graph with a cycle has the 3-clique as a minor, which from the statement in the previous section has treewidth 2. Since the partial 2-trees are closed under minors, the graph therefore has treewidth 2 or greater.

Definition

Treewidth

Graph minors

Dynamic programming

Treewidth of cliques

Treewidth of trees

See also