In graph-theoretic mathematics

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, a distance-hereditary graph (also called a completely separable graph) is a graph in which the distance

Distance

Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...

s in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.

Distance-hereditary graphs were named and first studied by , although an equivalent class of graphs was already shown to be perfect

Perfect graph

In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph....

 in 1970 by Olaru and Sachs.

It has been known for some time that the distance-hereditary graphs constitute an intersection class of graphs, but no intersection model was known until one was given by .

Definition and characterization

The original definition of a distance-hereditary graph is a graph G such that, if any two vertices u and v belong to a connected induced subgraph H of G, then some shortest path connecting u and v in G must be a subgraph of H, so that the distance between u and v in H is the same as the distance in G.

Distance-hereditary graphs may also be characterized in several other equivalent ways:

• They are the graphs in which every induced path is a shortest path, or equivalently the graphs in which every non-shortest path has at least one edge connecting two non-consecutive path vertices.

• They are the graphs in which every cycle of length at least five has two or more diagonals, and in which every cycle of length exactly five has at least one pair of crossing diagonals.

• They are the graphs in which every cycle of length five or more has at least one pair of crossing diagonals.

• They are the graphs in which, for every four vertices u, v, w, and x, at least two of the three sums of distances d(u,v)+d(w,x), d(u,w)+d(v,x), and d(u,x)+d(v,w) are equal to each other.

• They are the graphs that do not have as isometric subgraphs any cycle of length five or more, or any of three other graphs: a 5-cycle with one chord, a 5-cycle with two non-crossing chords, and a 6-cycle with a chord connecting opposite vertices.

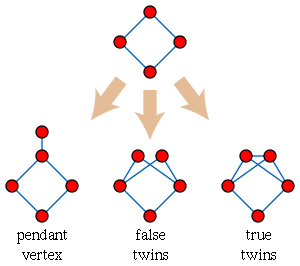
• They are the graphs that may be built up from a single vertex by a sequence of the following three operations, as shown in the illustration:
  1. Add a new pendant vertex connected by a single edge to an existing vertex of the graph.
  2. Replace any vertex of the graph by a pair of vertices, each of which has the same set of neighbors as the replaced vertex. The new pair of vertices are called false twins of each other.
  3. Replace any vertex of the graph by a pair of vertices, each of which has as its neighbors the neighbors of the replaced vertex together with the other vertex of the pair. The new pair of vertices are called true twins of each other.

• They are the graphs that may be completely decomposed into clique
  Clique
  A clique is an exclusive group of people who share common interests, views, purposes, patterns of behavior, or ethnicity. A clique as a reference group can be either normative or comparative. Membership in a clique is typically exclusive, and qualifications for membership may be social or...
  
  s and stars (complete bipartite graph
  Complete bipartite graph
  In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
  
  s K_1,q) by a split decomposition. In this decomposition, one finds a partition of the graph into two subsets, such that the edges separating the two subsets form a complete bipartite subgraph
  Complete bipartite graph
  In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
  
  , forms two smaller graphs by replacing each of the two sides of the partition by a single vertex, and recursively partitions these two subgraphs.

• They are the graphs that have rank-width one, where the rank-width of a graph is defined as the minimum, over all hierarchical partitions of the vertices of the graph, of the maximum rank among certain submatrices of the graph's adjacency matrix
  Adjacency matrix
  In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
  
   determined by the partition.

Relation to other graph families

Every distance-hereditary graph is a perfect graph

Perfect graph

In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph....

 and more specifically a perfectly orderable graph. Every distance-hereditary graph is also a parity graph, a graph in which every two induced paths between the same pair of vertices both have odd length or both have even length. Every even power of a distance-hereditary graph G (that is, the graph G²ⁱ formed by connecting pairs of vertices at distance at most 2i in G) is a chordal graph

Chordal graph

In the mathematical area of graph theory, a graph is chordal if each of its cycles of four or more nodes has a chord, which is an edge joining two nodes that are not adjacent in the cycle. An equivalent definition is that any chordless cycles have at most three nodes...

.

Every distance-hereditary graph may be represented as the intersection graph

Intersection graph

In the mathematical area of graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph may be represented as an intersection graph, but some important special classes of graphs may be defined by the types of sets that are used to form...

 of chords on a circle, forming a circle graph

Circle graph

In graph theory, a circle graph is the intersection graph of a set of chords of a circle. That is, it is an undirected graph whose vertices can be associated with chords of a circle such that two vertices are adjacent if and only if the corresponding chords cross each other.-Algorithmic...

. This may be seen by building up the graph by adding pendant vertices, false twins, and true twins, at each step building up a corresponding set of chords representing the graph. Adding a pendant vertex corresponds to adding a chord near the endpoints of an existing chord so that it crosses only that chord; adding false twins corresponds to replacing a chord by two parallel chords crossing the same set of other chords; and adding true twins corresponds to replacing a chord by two chords that cross each other but are nearly parallel and cross the same set of other chords.

A distance-hereditary graph is bipartite

Bipartite graph

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...

 if and only if it is triangle-free

Triangle-free graph

In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally...

. Bipartite distance-hereditary graphs may be built up from a single vertex by adding only pendant vertices and false twins, since any true twin would form a triangle, but the pendant vertex and false twin operations preserve bipartiteness.

The graphs that may be built from a single vertex by pendant vertices and true twins, without any false twin operations, are the chordal

Chordal graph

In the mathematical area of graph theory, a graph is chordal if each of its cycles of four or more nodes has a chord, which is an edge joining two nodes that are not adjacent in the cycle. An equivalent definition is that any chordless cycles have at most three nodes...

 distance-hereditary graphs, also called ptolemaic graphs; they include as a special case the block graph

Block graph

In graph theory, a branch of combinatorial mathematics, a block graph is a type of undirected graph in which every biconnected component is a clique...

s. The graphs that may be built from a single vertex by false twin and true twin operations, without any pendant vertices, are the cograph

Cograph

In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union...

s, which are therefore distance-hereditary; the cographs are exactly the disjoint unions of diameter-2 distance-hereditary graphs. The neighborhood of any vertex in a distance-hereditary graph is a cograph. The transitive closure of the directed graph formed by choosing any set of orientations for the edges of any tree

Tree (graph theory)

In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...

 is distance-hereditary; the special case in which the tree is oriented consistently away from some vertex forms a subclass of distance-hereditary graphs known as the trivially perfect graphs, which may equivalently be described as chordal cographs.

Algorithms

Distance-hereditary graphs may be recognized, and parsed into a sequence of pendant vertex and twin operations, in linear time.

Because distance-hereditary graphs are perfect, some optimization problems may be solved in polynomial time for them despite being NP-hard

NP-hard

NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...

 for more general classes of graphs. Thus, it is possible in polynomial time to find the maximum clique or maximum independent set in a distance-hereditary graph, or to find an optimal graph coloring

Graph coloring

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...

 of any distance-hereditary graph.
Because distance-hereditary graphs are circle graphs, they inherit polynomial time algorithms for circle graphs; for instance, it is possible determine in polynomial time the treewidth of any circle graph and therefore of any distance-hereditary graph.
Additionally, the clique-width

Clique-width

In graph theory, the clique-width of a graph G is the minimum number of labels needed to construct G by means of the following 4 operations :#Creation of a new vertex v with label i...

 of any distance-hereditary graph is at most three. As a consequence, efficient dynamic programming

Dynamic programming

In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...

 algorithms exist for many problems on these graphs.

Several other optimization problems may also be solved more efficiently using algorithms specifically designed for distance-hereditary graphs.
As show, a minimum connected dominating set

Connected dominating set

In graph theory, a connected dominated set and a maximum leaf spanning tree are two closely related structures defined on an undirected graph.-Definitions:A connected dominating set of a graph G is a set D of vertices with two properties:...

 (or equivalently a spanning tree

Spanning tree

Spanning tree can refer to:* Spanning tree , a tree which contains every vertex of a more general graph* Spanning tree protocol, a protocol for finding spanning trees in bridged networks...

 with the maximum possible number of leaves) may be found in polynomial time on a distance-hereditary graph.
A Hamiltonian cycle or Hamiltonian path of any distance-hereditary graph may also be found in polynomial time.