
Primitive root modulo n
Encyclopedia
In modular arithmetic
, a branch of number theory
, a primitive root modulo n is any number g with the property that any number coprime
to n is congruent to a power of g modulo n. In other words, g is a generator of the multiplicative group of integers modulo n
. That is, for every integer a coprime
to n, there is an integer k such that gk ≡ a (mod n). Such k is called the index or discrete logarithm
of a to the base g modulo n.
Gauss
defined primitive roots in Article 57 of the Disquisitiones Arithmeticae
(1801), where he credited Euler with coining the term. In Article 56 he stated that Lambert and Euler knew of them, but he was the first to rigorously demonstrate that primitive roots exist. In fact, the Disquisitiones contains two proofs: the one in Article 54 is a nonconstructive existence proof
, while the other in Article 55 is constructive
.
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
, a branch of number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a primitive root modulo n is any number g with the property that any number coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to n is congruent to a power of g modulo n. In other words, g is a generator of the multiplicative group of integers modulo n
Multiplicative group of integers modulo n
In modular arithmetic the set of congruence classes relatively prime to the modulus n form a group under multiplication called the multiplicative group of integers modulo n. It is also called the group of primitive residue classes modulo n. In the theory of rings, a branch of abstract algebra, it...
. That is, for every integer a coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to n, there is an integer k such that gk ≡ a (mod n). Such k is called the index or discrete logarithm
Discrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
of a to the base g modulo n.
Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
defined primitive roots in Article 57 of the Disquisitiones Arithmeticae
Disquisitiones Arithmeticae
The Disquisitiones Arithmeticae is a textbook of number theory written in Latin by Carl Friedrich Gauss in 1798 when Gauss was 21 and first published in 1801 when he was 24...
(1801), where he credited Euler with coining the term. In Article 56 he stated that Lambert and Euler knew of them, but he was the first to rigorously demonstrate that primitive roots exist. In fact, the Disquisitiones contains two proofs: the one in Article 54 is a nonconstructive existence proof
Existence theorem
In mathematics, an existence theorem is a theorem with a statement beginning 'there exist ..', or more generally 'for all x, y, ... there exist ...'. That is, in more formal terms of symbolic logic, it is a theorem with a statement involving the existential quantifier. Many such theorems will not...
, while the other in Article 55 is constructive
Constructive proof
In mathematics, a constructive proof is a method of proof that demonstrates the existence of a mathematical object with certain properties by creating or providing a method for creating such an object...
.
Elementary example
The number 3 is a primitive root modulo 7 because-

Here we see that the period of 3k modulo 7 is 6. The remainders in the period, which are 3, 2, 6, 4, 5, 1, form a rearrangement of all nonzero remainders modulo 7, implying that 3 is indeed a primitive root modulo 7. Curiously, permutations created in this way (and their circular shifts) have been shown to be Costas arrays.
Definition
If n is a positive integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
, the integers between 1 and n−1 which are coprimeCoprimeIn number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to n (or equivalently, the congruence classes coprimeCoprimeIn number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to n) form a groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
with multiplication moduloModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
n as the operation; it is denoted by Zn× and is called the group of units modulo n or the group of primitive classes modulo n. As explained in the article multiplicative group of integers modulo nMultiplicative group of integers modulo nIn modular arithmetic the set of congruence classes relatively prime to the modulus n form a group under multiplication called the multiplicative group of integers modulo n. It is also called the group of primitive residue classes modulo n. In the theory of rings, a branch of abstract algebra, it...
, this group is cyclicCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
n is equal to 1, 2, 4, pk, or 2 pk where pk is a power of an odd prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. A generatorGenerating set of a groupIn abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
of this cyclic group is called a primitive root modulo n, or a primitive element of Zn×.
The order of (i.e. the number of elements in) Zn× is given by Euler's totient functionEuler's totient functionIn number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
 Euler's theorem says that aφ(n) ≡ 1 (mod n) for every a coprime to n; the lowest power of a which is congruent to 1 modulo n is called the multiplicative orderMultiplicative orderIn number theory, given an integer a and a positive integer n with gcd = 1, the multiplicative order of a modulo n is the smallest positive integer k withThe order of a modulo n is usually written ordn, or On.- Example :To determine the multiplicative order of 4 modulo 7, we compute 42 = 16 ≡ 2 ...
Euler's theorem says that aφ(n) ≡ 1 (mod n) for every a coprime to n; the lowest power of a which is congruent to 1 modulo n is called the multiplicative orderMultiplicative orderIn number theory, given an integer a and a positive integer n with gcd = 1, the multiplicative order of a modulo n is the smallest positive integer k withThe order of a modulo n is usually written ordn, or On.- Example :To determine the multiplicative order of 4 modulo 7, we compute 42 = 16 ≡ 2 ...
of a modulo n. In particular, for a to be a primitive root modulo n, φ(n) has to be the smallest power of a which is congruent to 1 modulo n.
Examples
For example, if n = 14 then the elements of Zn× are the congruence classes {1, 3, 5, 9, 11, 13}; there are φ(14) = 6 of them. Here is a table of their powers modulo 14:
x x, x2, x3, ... (mod 14)
1 : 1
3 : 3, 9, 13, 11, 5, 1
5 : 5, 11, 13, 9, 3, 1
9 : 9, 11, 1
11 : 11, 9, 1
13 : 13, 1
The order of 1 is 1, the orders of 3 and 5 are 6, the orders of 9 and 11 are 3, and the order of 13 is 2. Thus, 3 and 5 are the primitive roots modulo 14.
For a second example let n = 15. The elements of Z15× are the congruence classes {1, 2, 4, 7, 8, 11, 13, 14}; there are φ(15) = 8 of them.
x x, x2, x3, ... (mod 15)
1 : 1
2 : 2, 4, 8, 1
4 : 4, 1
7 : 7, 4, 13, 1
8 : 8, 4, 2, 1
11 : 11, 1
13 : 13, 4, 7, 1
14 : 14, 1
Since there is no number whose order is 8, there are no primitive roots modulo 15.
Table of primitive roots
This is Gauss's table of the primitive roots from the Disquisitiones. Unlike most modern authors he did not always choose the smallest primitive root. Instead, he chose 10 if it is a primitive root; if it isn't, he chose whichever root gives 10 the smallest index, and, if there is more than one, chose the smallest of them. This is not only to make hand calculation easier, but is used in § VI where the periodic decimal expansions of rational numbers are investigated.
The rows of the table are labelled with the prime powers (excepting 2, 4, and 8) less than 100; the second column is a primitive root modulo that number. The columns are labelled with the primes less than 97. The entry in row p column q is the index of q modulo p for the given root.
For example, in row 11, 2 is given as the primitive root, and in column 5 the entry is 4. This means that 24 = 16 ≡ 5 (mod 11).
For the index of a composite number, add the indices of its prime factors.For example, in row 11, the index of 6 is the sum of the indices for 2 and 3: 21 + 8 = 512 ≡ 6 (mod 11). The index of 25 is twice the index 5: 28 = 256 ≡ 25 (mod 11). (Of course, since 25 ≡ 3 (mod 11), the entry for 3 is 8).
The table is straightforward for the odd prime powers. But the powers of 2, (16, 32, and 64) do not have primitive roots; instead, the powers of 5 account for one-half of the odd numbers less than the power of 2, and their negatives modulo the power of 2 account for the other half. All powers of 5 are ≡ 5 or 1 (mod 8); the columns headed by numbers ≡ 3 or 7 (mod 8) contain the index of its negative.
For example, modulo 32 the index for 7 is 2, and 52 = 25 ≡ –7 (mod 32), but the entry for 17 is 4, and 54 = 625 ≡ 17 (mod 32).
The sequence of smallest primitive roots may be found at .
Primitive roots and indices
(other columns are the indices of integers under respective column headings)n root 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 3 2 1 5 2 1 3 7 3 2 1 5 9 2 1 * 5 4 11 2 1 8 4 7 13 6 5 8 9 7 11 16 5 * 3 1 2 1 3 17 10 10 11 7 9 13 12 19 10 17 5 2 12 6 13 8 23 10 8 20 15 21 3 12 17 5 25 2 1 7 * 5 16 19 13 18 11 27 2 1 * 5 16 13 8 15 12 11 29 10 11 27 18 20 23 2 7 15 24 31 17 12 18 20 4 29 23 1 22 21 27 32 5 * 3 1 2 5 7 4 7 6 3 0 37 5 11 34 1 28 6 13 5 25 21 15 27 41 6 26 15 22 39 3 31 33 9 36 7 28 32 43 28 39 17 5 7 6 40 16 29 20 25 32 35 18 47 10 30 18 17 38 27 3 42 29 39 43 5 24 25 37 49 10 2 13 41 * 16 9 31 35 32 24 7 38 27 36 23 53 26 25 9 31 38 46 28 42 41 39 6 45 22 33 30 8 59 10 25 32 34 44 45 28 14 22 27 4 7 41 2 13 53 28 61 10 47 42 14 23 45 20 49 22 39 25 13 33 18 41 40 51 17 64 5 * 3 1 10 5 15 12 7 14 11 8 9 14 13 12 5 1 3 67 12 29 9 39 7 61 23 8 26 20 22 43 44 19 63 64 3 54 5 71 62 58 18 14 33 43 27 7 38 5 4 13 30 55 44 17 59 29 37 11 73 5 8 6 1 33 55 59 21 62 46 35 11 64 4 51 31 53 5 58 50 44 79 29 50 71 34 19 70 74 9 10 52 1 76 23 21 47 55 7 17 75 54 33 4 81 11 25 * 35 22 1 38 15 12 5 7 14 24 29 10 13 45 53 4 20 33 48 52 83 50 3 52 81 24 72 67 4 59 16 36 32 60 38 49 69 13 20 34 53 17 43 47 89 30 72 87 18 7 4 65 82 53 31 29 57 77 67 59 34 10 45 19 32 26 68 46 27 97 10 86 2 11 53 82 83 19 27 79 47 26 41 71 44 60 14 65 32 51 25 20 42 91 18 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89
Arithmetic facts
Gauss proved that for any prime number p (with the sole exception of p = 3), the product of its primitive roots is congruent to 1 modulo p.
He also proved that for any prime number p, the sum of its primitive roots is congruent to μ(p – 1) modulo p where μ is the Möbius functionMöbius functionThe classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
.
For example
- p = 3, μ(2) = –1. The primitive root is 2.
- p = 5, μ(4) = 0. The primitive roots are 2 and 3.
- p = 7, μ(6) = 1. The primitive roots are 3 and 5.
- p = 31, μ(30) = –1. The primitive roots are 3, 11, 12, 13, 17 ≡ –14, 21 ≡ –10, 22 ≡ –9, and 24 ≡ –7.
-
- Their product 970377408 ≡ 1 (mod 31) and their sum 123 ≡ –1 (mod 31).
-
- 3×11 = 33 ≡ 2
- 12×13 = 156 ≡ 1
- (–14)×(–10) = 140 ≡ 16
- (–9)×(–7) = 63 ≡ 1, and 2×1×16×1 = 32 ≡ 1 (mod 31).
Finding primitive roots
No simple general formula to compute primitive roots modulo n is known. There are however methods to locate a primitive root that are faster than simply trying out all candidates.
If the multiplicative orderMultiplicative orderIn number theory, given an integer a and a positive integer n with gcd = 1, the multiplicative order of a modulo n is the smallest positive integer k withThe order of a modulo n is usually written ordn, or On.- Example :To determine the multiplicative order of 4 modulo 7, we compute 42 = 16 ≡ 2 ...
of a number m modulo n is equal to (the order of Zn×), then it is a primitive root. In fact the converse is true: If m is a primitive root modulo n, then the multiplicative order of m is
(the order of Zn×), then it is a primitive root. In fact the converse is true: If m is a primitive root modulo n, then the multiplicative order of m is  . We can use this to test for primitive roots.
. We can use this to test for primitive roots.
First, compute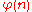 . Then determine the different prime factors of
. Then determine the different prime factors of 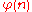 , say p1, ..., pk. Now, for every element m of Zn*, compute
, say p1, ..., pk. Now, for every element m of Zn*, compute
using a fast algorithm for modular exponentiationModular exponentiationModular exponentiation is a type of exponentiation performed over a modulus. It is particularly useful in computer science, especially in the field of cryptography....
such as exponentiation by squaringExponentiation by squaringExponentiating by squaring is a general method for fast computation of large integer powers of a number. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. In additive notation the appropriate term is double-and-add...
. A number m for which these k results are all different from 1 is a primitive root.
The number of primitive roots modulo n, if there are any, is equal to
since, in general, a cyclic group with r elements has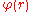 generators.
generators.
If g is a primitive root modulo p, then g is a primitive root modulo all powers pk unless g p – 1 ≡ 1 (mod p2); in that case, g + p is.
If g is a primitive root modulo pk, then g or g + pk (whichever one is odd) is a primitive root modulo 2pk.
Finding primitive roots modulo p is also equivalent to finding the roots of the (p-1)th cyclotomic polynomialCyclotomic polynomialIn algebra, the nth cyclotomic polynomial, for any positive integer n, is the monic polynomial:\Phi_n = \prod_\omega \,where the product is over all nth primitive roots of unity ω in a field, i.e...
modulo p.
Order of magnitude of primitive roots
The least primitive root modulo p is generally small.
Let gp be the smallest primitive root modulo p in the range 1, 2, ..., p–1.
Fridlander (1949) and Salié (1950) proved that there is a positive constant C such that for infinitely many primes gp > C log p.
It can be proved in an elementary manner that for any positive integer M there are infinitely many primes such that M < gp < p – M.
Burgess (1962) proved that for every ε > 0 there is a C such that
GrosswaldEmil GrosswaldEmil Grosswald was a Romanian-American mathematician who worked primarily in number theory. His career is closely associated with that of his teacher, Hans Rademacher.- Life and education :...
(1981) proved that if , then
, then  .
.
Shoup (1990, 1992) proved, assuming the generalized Riemann hypothesisGeneralized Riemann hypothesisThe Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function...
, that gp =O(log6 p).
Applications
Primitive root modulo n is often used in cryptographyCryptographyCryptography is the practice and study of techniques for secure communication in the presence of third parties...
, including the Diffie–Hellman key exchange scheme.
See also
- Artin's conjecture on primitive rootsArtin's conjecture on primitive rootsIn number theory, Artin's conjecture on primitive roots states that a given integer a which is not a perfect square and not −1 is a primitive root modulo infinitely many primes p. The conjecture also ascribes an asymptotic density to these primes...
- Dirichlet characterDirichlet characterIn number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of \mathbb Z / k \mathbb Z...
- Gauss's generalization of Wilson's theorem
- Multiplicative orderMultiplicative orderIn number theory, given an integer a and a positive integer n with gcd = 1, the multiplicative order of a modulo n is the smallest positive integer k withThe order of a modulo n is usually written ordn, or On.- Example :To determine the multiplicative order of 4 modulo 7, we compute 42 = 16 ≡ 2 ...
- Root of unity modulo n
External links
- This site has a primitive root calculator applet.
- A calculator of all primitive roots modulo p is located here.

