Mathematical jargon
Encyclopedia
The language of mathematics has a vast vocabulary
of specialist and technical terms. It also has a certain amount of jargon
: commonly used phrases which are part of the culture of mathematics, rather than of the subject. Jargon often appears in lectures, and sometimes in print, as informal shorthand for rigorous arguments or precise ideas. Much of this is common English, but with a specific non-obvious meaning when used in a mathematical sense.
Note that some phrases, like "in general", appear below in more than one section.
abstract nonsense
: Also general abstract nonsense or generalized abstract nonsense, a tongue-in-cheek reference to category theory
, using which one can employ arguments that establish a (possibly concrete) result without reference to any specifics of the present problem.
canonical: A reference to a standard or choice-free presentation of some mathematical object. The term canonical is also used more informally, meaning roughly "standard" or "classic". For example, one might say that Euclid
's proof is the "canonical proof" of the infinitude of primes.
deep: A result is called "deep" if its proof requires concepts and methods that are advanced beyond the concepts needed to formulate the result. The prime number theorem
, proved with techniques from complex analysis
, was thought to be a deep result until elementary proof
s were found. The fact that π is irrational is a deep result because it requires considerable development of real analysis
to prove, even though it can be stated in terms of simple number theory and geometry.
elegant
: Also beautiful; an aesthetic term referring to the ability of an idea to provide insight into mathematics, whether by unifying disparate fields, introducing a new perspective on a single field, or providing a technique of proof which is either particularly simple, or captures the intuition or imagination as to why the result it proves is true. Gian-Carlo Rota
distinguished between elegance of presentation and beauty of concept, saying that for example, some topics could be written about elegantly although the mathematical content is not beautiful, and some theorems or proofs are beautiful but may be written about inelegantly.
elementary
: A proof or result is called "elementary" if it requires only basic concepts and methods, in contrast to so-called deep results. The concept of "elementary proof" is used specifically in number theory
, where it usually refers to a proof that does not use methods from complex analysis
.
: A result is called "folklore" if it is non-obvious, has not been published, and yet is generally known among the specialists in a field. Usually, it is unknown who first obtained the result. If the result is important, it may eventually find its way into the textbooks, whereupon it ceases to be folklore.
natural
: Similar to "canonical" but more specific, this term makes reference to a description (almost exclusively in the context of transformation
s) which holds independently of any choices. Though long used informally, this term has found a formal definition in category theory.
pathological
: An object behaves pathologically if it fails to conform to the generic behavior of such objects, fails to satisfy certain regularity properties (depending on context), or simply disobeys mathematical intuition. These can be and often are contradictory requirements. Sometimes the term is more pointed, referring to an object which is specifically and artificially exhibited as a counterexample to these properties.
rigor (rigour): Mathematics strives to establish its results using indisputable logic rather than informal descriptive argument. Rigor is the use of such logic in a proof.
well-behaved
: An object is well-behaved (in contrast with being pathological) if it does satisfy the prevailing regularity properties, or sometimes if it conforms to intuition (but intuition often suggests the opposite behavior as well).
almost all
: A shorthand term for "all except for a set of measure zero", when there is a measure to speak of. For example, "almost all real numbers are transcendental
" because the algebraic real numbers form a countable subset of the real numbers with measure zero. One can also speak of "almost all" integers having a property to mean "all but finitely many", despite the integers not admitting a measure for which this agrees with the previous usage. For example, "almost all prime number
s are odd". There is a more complicated meaning for integers as well, discussed in the main article. Finally, this term is sometimes used synonymously with generic, below.
arbitrarily large
: Notions which arise mostly in the context of limits, referring to the recurrence of a phenomenon as the limit is approached. A statement such as that predicate P is satisfied by arbitrarily large values, can be expressed in more formal notation by . See also frequently. The statement that quantity f(x) depending on x "can be made" arbitrarily large, corresponds to .
arbitrary
: A shorthand for the universal quantifier. An arbitrary choice is one which is made unrestrictedly, or alternatively, a statement holds of an arbitrary element of a set if it holds of any element of that set.
eventually, definitely: In the context of limits, this is shorthand for for sufficiently large arguments; the relevant argument(s) are implicit in the context. As an example, one could say that "The function log(log(x)) eventually becomes larger than 100"; in this context, "eventually" means "for sufficiently large x".
factor through: A term in category theory
referring to composition of morphisms. If we have three objects A, B, and C and a map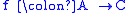
which is written as a composition 
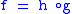with 
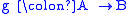and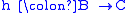 
, then f is said to factor through any (and all) of 
, 
, and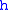 
.
finite: Next to the usual meaning of "not infinite", in another more restrictive meaning that one may encounter, a value being said to be "finite" also excludes infinitesimal
values and the value 0. For example, if the variance
of a random variable is said to be finite, this implies it is a positive real number.
frequently: In the context of limits, this is shorthand for for arbitrarily large arguments and its relatives; as with eventually, the intended variant is implicit. As an example, one could say that "The function sin(x) is frequently zero", where "frequently" means "for arbitrarily large x".
generic
: This term has similar connotations as almost all but is used particularly for concepts outside the purview of measure theory. A property holds "generically" on a set if the set satisfies some (context-dependent) notion of density, or perhaps if its complement satisfies some (context-dependent) notion of smallness. For example, a property which holds on a dense
Gδ (intersection of countably many open sets) is said to hold generically. In algebraic geometry
, one says that a property of points on an algebraic variety
that holds on a dense Zariski open
set is true generically; however, it is usually not said that a property which holds merely on a dense set (which is not Zariski open) is generic in this situation.
in general: In a descriptive context, this phrase introduces a simple characterization of a broad class of objects, with an eye towards identifying a unifying principle. This term introduces an "elegant" description which holds for "arbitrary" objects. Exceptions to this description may be mentioned explicitly, as "pathological" cases.
left-hand side, right-hand side
(LHS, RHS): Most often, these refer simply to the left-hand or the right-hand side of an equation; for example,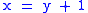
has x on the LHS and y + 1 on the RHS. Occasionally, these are used in the sense of lvalue
and rvalue: an RHS is primitive, and an LHS is derivative.
nice: A mathematical object is colloquially called nice or sufficiently nice if it satisfies hypotheses or properties, sometimes unspecified or even unknown, that are especially desirable in a given context. It is an informal antonym for pathological. For example, one might conjecture that a differential operator ought to satisfy a certain boundedness condition "for nice test functions," or one might state that some interesting topological invariant should be computable "for nice spaces X."
proper: If, for some notion of substructure, objects are substructures of themselves (that is, the relationship is reflexive), then the qualification proper requires the objects to be different. For example, a proper subset of a set S is a subset
of S that is different from S, and a proper divisor of a number n is a divisor of n that is different from n. This overloaded
word is also non-jargon for a proper morphism.
regular : A function is called regular if it satisfies satisfactory continuity and differentiability properties, which are often context-dependent. These properties might include possessing a specified number of derivatives, with the function and its derivatives exhibiting some nice property, such as Hölder continuity. Informally, this term is sometimes used synonymously with smooth, below. These imprecise uses of the word regular are not to be confused with the notion of a regular topological space
, which is rigorously defined.
resp.: (Respectively) A convention to shorten parallel expositions. "A (resp. B) [has some relationship to] X (resp. Y)" means that A [has some relationship to] X and also that B [has (the same) relationship to] Y. For example, squares (resp. triangles) have 4 sides (resp. 3 sides); or compact (resp. Lindelof) spaces are ones where every open cover has a finite (resp. countable) open subcover.
sharp: Often, a mathematical theorem will establish constraints on the behavior of some object; for example, a function will be shown to have an upper or lower bound. The constraint is sharp (sometimes optimal) if it cannot be made more restrictive without failing in some cases. For example, for arbitrary nonnegative real numbers x, the exponential function ex, where e = 2.7182818..., gives an upper bound on the values of the quadratic function x2. This is not sharp; the gap between the functions is everywhere at least 1. Among the exponential functions of the form αx, setting α = e2/e = 2.0870652... results in a sharp upper bound; the slightly smaller choice α = 2 fails to produce an upper bound, since then α3 = 8 < 32.
smooth
: Smoothness is a concept which mathematics has endowed with many meanings, from simple differentiability to infinite differentiability to analyticity, and still others which are more complicated. Each such usage attempts to invoke the physically intuitive notion of smoothness.
strong, stronger: A theorem is said to be strong if it deduces restrictive results from general hypotheses. One celebrated example is Donaldson's theorem
, which puts tight restraints on what would otherwise appear to be a large class of manifolds. This (informal) usage reflects the opinion of the mathematical community: not only should such a theorem be strong in the descriptive sense (below) but it should also be definitive in its area. A theorem, result, or condition is further called stronger than another one if a proof of the second can be easily obtained from the first. An example is the sequence of theorems: Fermat's little theorem
, Euler's theorem, Lagrange's theorem
, each of which is stronger than the last; another is that a sharp upper bound (see above) is a stronger result than a non-sharp one. Finally, the adjective strong or the adverb strongly may be added to a mathematical notion to indicate a related stronger notion; for example, a strong antichain is an antichain
satisfying certain additional conditions, and likewise a strongly regular graph
is a regular graph
meeting stronger conditions. When used in this way, the stronger notion (such as "strong antichain") is a technical term with a precisely defined meaning; the nature of the extra conditions cannot be derived from the definition of the weaker notion (such as "antichain").
sufficiently large, suitably small, sufficiently close: In the context of limits, these terms refer to some (unspecified, even unknown) point at which a phenomenon prevails as the limit is approached. A statement such as that predicate P holds for sufficiently large values, can be expressed in more formal notation by ∃x : ∀y ≥ x : P(y). See also eventually.
upstairs, downstairs: A descriptive term referring to notation in which two objects are written one above the other; the upper one is upstairs and the lower, downstairs. For example, in a fiber bundle
, the total space is often said to be upstairs, with the base space downstairs. In a fraction
, the numerator is occasionally referred to as upstairs and the denominator downstairs, as in "bringing a term upstairs".
up to
, modulo, mod out by: An extension to mathematical discourse of the notions of modular arithmetic
. A statement is true up to a condition if the establishment of that condition is the only impediment to the truth of the statement.
vanish: To assume the value 0. For example, "The function sin(x) vanishes for those values of x that are integer multiples of π." This can also apply to limits: see Vanish at infinity.
weak, weaker: The converse of strong.
aliter: An obsolescent term which is used to announce to the reader an alternative method, or proof of a result. In a proof it therefore flags a piece of reasoning that is superfluous from a logical point of view, but has some other interest.
by way of contradiction (BWOC), or "for, if not, ...": The rhetorical prelude to a proof by contradiction, preceding the negation of the statement to be proved.
if and only if (iff): An abbreviation for logical equivalence
of statements.
in general: In the context of proofs, this phrase is often seen in induction
arguments when passing from the base case to the "induction step", and similarly, in the definition of sequences whose first few terms are exhibited as examples of the formula giving every term of the sequence.
necessary and sufficient: A minor variant on "if and only if"; necessary means "only if" and sufficient means '"if". For example, "For a field
K to be algebraically closed
it is necessary and sufficient that it have no finite field extension
s" means "K is algebraically closed if and only if it has no finite extensions". Often used in lists, as in "The following conditions are necessary and sufficient for a field to be algebraically closed...".
need to show (NTS), required to prove (RTP), wish to show, want to show (WTS): Proofs sometimes proceed by enumerating several conditions whose satisfaction will together imply the desired theorem; thus, one needs to show just these statements.
one and only one: An statement of the uniqueness of an object; the object exists, and furthermore, no other such object exists.
Q.E.D.
: (Quod erat demonstrandum): A Latin abbreviation, meaning "which was to be demonstrated", historically placed at the end of proofs, but less common currently.
sufficiently nice: A condition on objects in the scope of the discussion, to be specified later, that will guarantee that some stated property holds for them. When working out a theorem, the use of this expression in the statement of the theorem indicates that the conditions involved may be not yet known to the speaker, and that the intent is to collect the conditions that will be found to be needed in order for the proof of the theorem to go through.
the following are equivalent (TFAE): Often several equivalent conditions (especially for a definition, such as normal subgroup
) are equally useful in practice; one introduces a theorem stating an equivalence of more than two statements with TFAE.
transport of structure
: It is often the case that two objects are shown to be equivalent in some way, and that one of them is endowed with additional structure. Using the equivalence, we may define such a structure on the second object as well, via transport of structure. For example, any two vector space
s of the same dimension are isomorphic; if one of them is given an inner product and if we fix a particular isomorphism, then we may define an inner product on the other space by factoring through the isomorphism.
without (any) loss of generality
(WLOG, WOLOG, WALOG), we may assume (WMA), it may be assumed that (WOLOGIMBAT): Sometimes a proposition can be more easily proved with additional assumptions on the objects it concerns. If the proposition as stated follows from this modified one with a simple and minimal explanation (for example, if the remaining special cases are identical but for notation), then the modified assumptions are introduced with this phrase and the altered proposition is proved.
angle chasing: Used to describe a geometrical proof that involves finding relationships between the various angles in a diagram.
back-of-the-envelope calculation
: An informal computation omitting much rigor without sacrificing correctness. Often this computation is "proof of concept" and treats only an accessible special case.
by inspection: A rhetorical shortcut made by authors who invite the reader to verify, at a glance, the correctness of a proposed expression or deduction. If an expression can be evaluated by straightforward application of simple techniques and without recourse to extended calculation or general theory, then it can be evaluated by inspection. It is also applied to solving equations; for example to find roots of a quadratic equation
by inspection is to 'notice' them, or mentally check them. 'By inspection' can play a kind of gestalt role: the answer or solution simply clicks into place.
clearly, can be easily shown: A term which shortcuts around calculation the mathematician perceives to be tedious or routine, accessible to any member of the audience with the necessary expertise in the field; Laplace used obvious (French
: évident).
diagram chasing: Given a commutative diagram
of objects and morphisms between them, if one wishes to prove some property of the morphisms (such as injectivity) which can be stated in terms of element
s, then the proof can proceed by tracing the path of elements of various objects around the diagram as successive morphisms are applied to it. That is, one chases elements around the diagram, or does a diagram chase.
handwaving
: A non-technique of proof mostly employed in lectures, where formal argument is not strictly necessary. It proceeds by omission of details or even significant ingredients, and is merely a plausibility argument.
: In a context not requiring rigor, this phrase often appears as a labor-saving device when the technical details of a complete argument would outweigh the conceptual benefits. The author gives a proof in a simple enough case that the computations are reasonable, and then indicates that "in general" the proof is similar.
morally true: Used to indicate that the speaker believes a statement should be true, given their mathematical experience, even though a proof has not yet been put forward. As a variation, the statement may in fact be false, but instead provide a slogan for or illustration of a correct principle. Hasse
's local-global principle is a particularly influential example of this.
trivial
: Similar to clearly. A concept is trivial if it holds by definition, is immediately corollary to a known statement, or is a simple special case of a more general concept.
Vocabulary
A person's vocabulary is the set of words within a language that are familiar to that person. A vocabulary usually develops with age, and serves as a useful and fundamental tool for communication and acquiring knowledge...
of specialist and technical terms. It also has a certain amount of jargon
Jargon
Jargon is terminology which is especially defined in relationship to a specific activity, profession, group, or event. The philosophe Condillac observed in 1782 that "Every science requires a special language because every science has its own ideas." As a rationalist member of the Enlightenment he...
: commonly used phrases which are part of the culture of mathematics, rather than of the subject. Jargon often appears in lectures, and sometimes in print, as informal shorthand for rigorous arguments or precise ideas. Much of this is common English, but with a specific non-obvious meaning when used in a mathematical sense.
Note that some phrases, like "in general", appear below in more than one section.
Philosophy of mathematics
These terms discuss mathematics as mathematicians think of it; they connote common intellectual strategies or notions the investigation of which somehow underlies much of mathematics.abstract nonsense
Abstract nonsense
In mathematics, abstract nonsense, general abstract nonsense, and general nonsense are terms used facetiously by some mathematicians to describe certain kinds of arguments and methods related to category theory. roughly speaking, category theory is the study of the general form of mathematical...
: Also general abstract nonsense or generalized abstract nonsense, a tongue-in-cheek reference to category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, using which one can employ arguments that establish a (possibly concrete) result without reference to any specifics of the present problem.
canonical: A reference to a standard or choice-free presentation of some mathematical object. The term canonical is also used more informally, meaning roughly "standard" or "classic". For example, one might say that Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
's proof is the "canonical proof" of the infinitude of primes.
deep: A result is called "deep" if its proof requires concepts and methods that are advanced beyond the concepts needed to formulate the result. The prime number theorem
Prime number theorem
In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
, proved with techniques from complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, was thought to be a deep result until elementary proof
Elementary proof
In mathematics, an elementary proof is a mathematical proof that only uses basic techniques. More specifically, the term is used in number theory to refer to proofs that make no use of complex analysis. For some time it was thought that certain theorems, like the prime number theorem, could only be...
s were found. The fact that π is irrational is a deep result because it requires considerable development of real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
to prove, even though it can be stated in terms of simple number theory and geometry.
elegant
Mathematical beauty
Many mathematicians derive aesthetic pleasure from their work, and from mathematics in general. They express this pleasure by describing mathematics as beautiful. Sometimes mathematicians describe mathematics as an art form or, at a minimum, as a creative activity...
: Also beautiful; an aesthetic term referring to the ability of an idea to provide insight into mathematics, whether by unifying disparate fields, introducing a new perspective on a single field, or providing a technique of proof which is either particularly simple, or captures the intuition or imagination as to why the result it proves is true. Gian-Carlo Rota
Gian-Carlo Rota
Gian-Carlo Rota was an Italian-born American mathematician and philosopher.-Life:Rota was born in Vigevano, Italy...
distinguished between elegance of presentation and beauty of concept, saying that for example, some topics could be written about elegantly although the mathematical content is not beautiful, and some theorems or proofs are beautiful but may be written about inelegantly.
elementary
Elementary proof
In mathematics, an elementary proof is a mathematical proof that only uses basic techniques. More specifically, the term is used in number theory to refer to proofs that make no use of complex analysis. For some time it was thought that certain theorems, like the prime number theorem, could only be...
: A proof or result is called "elementary" if it requires only basic concepts and methods, in contrast to so-called deep results. The concept of "elementary proof" is used specifically in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, where it usually refers to a proof that does not use methods from complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
.
: A result is called "folklore" if it is non-obvious, has not been published, and yet is generally known among the specialists in a field. Usually, it is unknown who first obtained the result. If the result is important, it may eventually find its way into the textbooks, whereupon it ceases to be folklore.
natural
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
: Similar to "canonical" but more specific, this term makes reference to a description (almost exclusively in the context of transformation
Transformation (mathematics)
In mathematics, a transformation could be any function mapping a set X on to another set or on to itself. However, often the set X has some additional algebraic or geometric structure and the term "transformation" refers to a function from X to itself that preserves this structure.Examples include...
s) which holds independently of any choices. Though long used informally, this term has found a formal definition in category theory.
pathological
Pathological (mathematics)
In mathematics, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive; the opposite is well-behaved....
: An object behaves pathologically if it fails to conform to the generic behavior of such objects, fails to satisfy certain regularity properties (depending on context), or simply disobeys mathematical intuition. These can be and often are contradictory requirements. Sometimes the term is more pointed, referring to an object which is specifically and artificially exhibited as a counterexample to these properties.
rigor (rigour): Mathematics strives to establish its results using indisputable logic rather than informal descriptive argument. Rigor is the use of such logic in a proof.
well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
: An object is well-behaved (in contrast with being pathological) if it does satisfy the prevailing regularity properties, or sometimes if it conforms to intuition (but intuition often suggests the opposite behavior as well).
Descriptive informalities
Although ultimately every mathematical argument must meet a high standard of precision, mathematicians use descriptive but informal statements to discuss recurring themes or concepts with unwieldy formal statements. Note that many of the terms are completely rigorous in context.almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
: A shorthand term for "all except for a set of measure zero", when there is a measure to speak of. For example, "almost all real numbers are transcendental
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
" because the algebraic real numbers form a countable subset of the real numbers with measure zero. One can also speak of "almost all" integers having a property to mean "all but finitely many", despite the integers not admitting a measure for which this agrees with the previous usage. For example, "almost all prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s are odd". There is a more complicated meaning for integers as well, discussed in the main article. Finally, this term is sometimes used synonymously with generic, below.
arbitrarily large
Arbitrarily large
In mathematics, the phrase arbitrarily large, arbitrarily small, arbitrarily long is used in statements such as:which is shorthand for:This should not be confused with the phrase "sufficiently large"...
: Notions which arise mostly in the context of limits, referring to the recurrence of a phenomenon as the limit is approached. A statement such as that predicate P is satisfied by arbitrarily large values, can be expressed in more formal notation by . See also frequently. The statement that quantity f(x) depending on x "can be made" arbitrarily large, corresponds to .
arbitrary
Arbitrary
Arbitrariness is a term given to choices and actions subject to individual will, judgment or preference, based solely upon an individual's opinion or discretion.Arbitrary decisions are not necessarily the same as random decisions...
: A shorthand for the universal quantifier. An arbitrary choice is one which is made unrestrictedly, or alternatively, a statement holds of an arbitrary element of a set if it holds of any element of that set.
eventually, definitely: In the context of limits, this is shorthand for for sufficiently large arguments; the relevant argument(s) are implicit in the context. As an example, one could say that "The function log(log(x)) eventually becomes larger than 100"; in this context, "eventually" means "for sufficiently large x".
factor through: A term in category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
referring to composition of morphisms. If we have three objects A, B, and C and a map
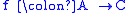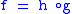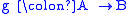which is written as a composition with and 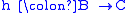, then f is said to factor through any (and all) of , , and 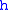.finite: Next to the usual meaning of "not infinite", in another more restrictive meaning that one may encounter, a value being said to be "finite" also excludes infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
values and the value 0. For example, if the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of a random variable is said to be finite, this implies it is a positive real number.
frequently: In the context of limits, this is shorthand for for arbitrarily large arguments and its relatives; as with eventually, the intended variant is implicit. As an example, one could say that "The function sin(x) is frequently zero", where "frequently" means "for arbitrarily large x".
generic
Generic property
In mathematics, properties that hold for "typical" examples are called generic properties. For instance, a generic property of a class of functions is one that is true of "almost all" of those functions, as in the statements, "A generic polynomial does not have a root at zero," or "A generic...
: This term has similar connotations as almost all but is used particularly for concepts outside the purview of measure theory. A property holds "generically" on a set if the set satisfies some (context-dependent) notion of density, or perhaps if its complement satisfies some (context-dependent) notion of smallness. For example, a property which holds on a dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
Gδ (intersection of countably many open sets) is said to hold generically. In algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, one says that a property of points on an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
that holds on a dense Zariski open
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
set is true generically; however, it is usually not said that a property which holds merely on a dense set (which is not Zariski open) is generic in this situation.
in general: In a descriptive context, this phrase introduces a simple characterization of a broad class of objects, with an eye towards identifying a unifying principle. This term introduces an "elegant" description which holds for "arbitrary" objects. Exceptions to this description may be mentioned explicitly, as "pathological" cases.
left-hand side, right-hand side
Sides of an equation
In mathematics, LHS is informal shorthand for the left-hand side of an equation. Similarly, RHS is the right-hand side. Each is solely a name for a term as part of an expression; and they are in practice interchangeable, since equality is symmetric...
(LHS, RHS): Most often, these refer simply to the left-hand or the right-hand side of an equation; for example,
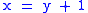has x on the LHS and y + 1 on the RHS. Occasionally, these are used in the sense of lvalueValue (computer science)
In computer science, a value is an expression which cannot be evaluated any further . The members of a type are the values of that type. For example, the expression "1 + 2" is not a value as it can be reduced to the expression "3"...
and rvalue: an RHS is primitive, and an LHS is derivative.
nice: A mathematical object is colloquially called nice or sufficiently nice if it satisfies hypotheses or properties, sometimes unspecified or even unknown, that are especially desirable in a given context. It is an informal antonym for pathological. For example, one might conjecture that a differential operator ought to satisfy a certain boundedness condition "for nice test functions," or one might state that some interesting topological invariant should be computable "for nice spaces X."
proper: If, for some notion of substructure, objects are substructures of themselves (that is, the relationship is reflexive), then the qualification proper requires the objects to be different. For example, a proper subset of a set S is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of S that is different from S, and a proper divisor of a number n is a divisor of n that is different from n. This overloaded
Operator overloading
In object oriented computer programming, operator overloading—less commonly known as operator ad-hoc polymorphism—is a specific case of polymorphism, where different operators have different implementations depending on their arguments...
word is also non-jargon for a proper morphism.
regular : A function is called regular if it satisfies satisfactory continuity and differentiability properties, which are often context-dependent. These properties might include possessing a specified number of derivatives, with the function and its derivatives exhibiting some nice property, such as Hölder continuity. Informally, this term is sometimes used synonymously with smooth, below. These imprecise uses of the word regular are not to be confused with the notion of a regular topological space
Regular space
In topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
, which is rigorously defined.
resp.: (Respectively) A convention to shorten parallel expositions. "A (resp. B) [has some relationship to] X (resp. Y)" means that A [has some relationship to] X and also that B [has (the same) relationship to] Y. For example, squares (resp. triangles) have 4 sides (resp. 3 sides); or compact (resp. Lindelof) spaces are ones where every open cover has a finite (resp. countable) open subcover.
sharp: Often, a mathematical theorem will establish constraints on the behavior of some object; for example, a function will be shown to have an upper or lower bound. The constraint is sharp (sometimes optimal) if it cannot be made more restrictive without failing in some cases. For example, for arbitrary nonnegative real numbers x, the exponential function ex, where e = 2.7182818..., gives an upper bound on the values of the quadratic function x2. This is not sharp; the gap between the functions is everywhere at least 1. Among the exponential functions of the form αx, setting α = e2/e = 2.0870652... results in a sharp upper bound; the slightly smaller choice α = 2 fails to produce an upper bound, since then α3 = 8 < 32.
smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
: Smoothness is a concept which mathematics has endowed with many meanings, from simple differentiability to infinite differentiability to analyticity, and still others which are more complicated. Each such usage attempts to invoke the physically intuitive notion of smoothness.
strong, stronger: A theorem is said to be strong if it deduces restrictive results from general hypotheses. One celebrated example is Donaldson's theorem
Donaldson's theorem
In mathematics, Donaldson's theorem states that a definite intersection form of a simply connected smooth manifold of dimension 4 is diagonalisable. If the intersection form is positive definite, it can be diagonalized to the identity matrix...
, which puts tight restraints on what would otherwise appear to be a large class of manifolds. This (informal) usage reflects the opinion of the mathematical community: not only should such a theorem be strong in the descriptive sense (below) but it should also be definitive in its area. A theorem, result, or condition is further called stronger than another one if a proof of the second can be easily obtained from the first. An example is the sequence of theorems: Fermat's little theorem
Fermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
, Euler's theorem, Lagrange's theorem
Lagrange's theorem (group theory)
Lagrange's theorem, in the mathematics of group theory, states that for any finite group G, the order of every subgroup H of G divides the order of G. The theorem is named after Joseph Lagrange....
, each of which is stronger than the last; another is that a sharp upper bound (see above) is a stronger result than a non-sharp one. Finally, the adjective strong or the adverb strongly may be added to a mathematical notion to indicate a related stronger notion; for example, a strong antichain is an antichain
Antichain
In mathematics, in the area of order theory, an antichain is a subset of a partially ordered set such that any two elements in the subset are incomparable. Let S be a partially ordered set...
satisfying certain additional conditions, and likewise a strongly regular graph
Strongly regular graph
In graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
is a regular graph
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
meeting stronger conditions. When used in this way, the stronger notion (such as "strong antichain") is a technical term with a precisely defined meaning; the nature of the extra conditions cannot be derived from the definition of the weaker notion (such as "antichain").
sufficiently large, suitably small, sufficiently close: In the context of limits, these terms refer to some (unspecified, even unknown) point at which a phenomenon prevails as the limit is approached. A statement such as that predicate P holds for sufficiently large values, can be expressed in more formal notation by ∃x : ∀y ≥ x : P(y). See also eventually.
upstairs, downstairs: A descriptive term referring to notation in which two objects are written one above the other; the upper one is upstairs and the lower, downstairs. For example, in a fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
, the total space is often said to be upstairs, with the base space downstairs. In a fraction
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
, the numerator is occasionally referred to as upstairs and the denominator downstairs, as in "bringing a term upstairs".
up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
, modulo, mod out by: An extension to mathematical discourse of the notions of modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
. A statement is true up to a condition if the establishment of that condition is the only impediment to the truth of the statement.
vanish: To assume the value 0. For example, "The function sin(x) vanishes for those values of x that are integer multiples of π." This can also apply to limits: see Vanish at infinity.
weak, weaker: The converse of strong.
Proof terminology
The formal language of proof draws repeatedly from a small pool of ideas, many of which are invoked through various lexical shorthands in practice.aliter: An obsolescent term which is used to announce to the reader an alternative method, or proof of a result. In a proof it therefore flags a piece of reasoning that is superfluous from a logical point of view, but has some other interest.
by way of contradiction (BWOC), or "for, if not, ...": The rhetorical prelude to a proof by contradiction, preceding the negation of the statement to be proved.
if and only if (iff): An abbreviation for logical equivalence
Logical equivalence
In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
of statements.
in general: In the context of proofs, this phrase is often seen in induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
arguments when passing from the base case to the "induction step", and similarly, in the definition of sequences whose first few terms are exhibited as examples of the formula giving every term of the sequence.
necessary and sufficient: A minor variant on "if and only if"; necessary means "only if" and sufficient means '"if". For example, "For a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K to be algebraically closed
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
it is necessary and sufficient that it have no finite field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
s" means "K is algebraically closed if and only if it has no finite extensions". Often used in lists, as in "The following conditions are necessary and sufficient for a field to be algebraically closed...".
need to show (NTS), required to prove (RTP), wish to show, want to show (WTS): Proofs sometimes proceed by enumerating several conditions whose satisfaction will together imply the desired theorem; thus, one needs to show just these statements.
one and only one: An statement of the uniqueness of an object; the object exists, and furthermore, no other such object exists.
Q.E.D.
Q.E.D.
Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...
: (Quod erat demonstrandum): A Latin abbreviation, meaning "which was to be demonstrated", historically placed at the end of proofs, but less common currently.
sufficiently nice: A condition on objects in the scope of the discussion, to be specified later, that will guarantee that some stated property holds for them. When working out a theorem, the use of this expression in the statement of the theorem indicates that the conditions involved may be not yet known to the speaker, and that the intent is to collect the conditions that will be found to be needed in order for the proof of the theorem to go through.
the following are equivalent (TFAE): Often several equivalent conditions (especially for a definition, such as normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
) are equally useful in practice; one introduces a theorem stating an equivalence of more than two statements with TFAE.
transport of structure
Transport of structure
In mathematics, transport of structure is the definition of a new structure on an object by reference to another object on which a similar structure already exists...
: It is often the case that two objects are shown to be equivalent in some way, and that one of them is endowed with additional structure. Using the equivalence, we may define such a structure on the second object as well, via transport of structure. For example, any two vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s of the same dimension are isomorphic; if one of them is given an inner product and if we fix a particular isomorphism, then we may define an inner product on the other space by factoring through the isomorphism.
without (any) loss of generality
Without loss of generality
Without loss of generality is a frequently used expression in mathematics...
(WLOG, WOLOG, WALOG), we may assume (WMA), it may be assumed that (WOLOGIMBAT): Sometimes a proposition can be more easily proved with additional assumptions on the objects it concerns. If the proposition as stated follows from this modified one with a simple and minimal explanation (for example, if the remaining special cases are identical but for notation), then the modified assumptions are introduced with this phrase and the altered proposition is proved.
Proof techniques
Mathematicians have several phrases to describe proofs or proof techniques. These are often used as hints for filling in tedious details.angle chasing: Used to describe a geometrical proof that involves finding relationships between the various angles in a diagram.
back-of-the-envelope calculation
Back-of-the-envelope calculation
A back-of-the-envelope calculation is a rough calculation, typically jotted down on any available scrap of paper such as the actual back of an envelope...
: An informal computation omitting much rigor without sacrificing correctness. Often this computation is "proof of concept" and treats only an accessible special case.
by inspection: A rhetorical shortcut made by authors who invite the reader to verify, at a glance, the correctness of a proposed expression or deduction. If an expression can be evaluated by straightforward application of simple techniques and without recourse to extended calculation or general theory, then it can be evaluated by inspection. It is also applied to solving equations; for example to find roots of a quadratic equation
Quadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
by inspection is to 'notice' them, or mentally check them. 'By inspection' can play a kind of gestalt role: the answer or solution simply clicks into place.
clearly, can be easily shown: A term which shortcuts around calculation the mathematician perceives to be tedious or routine, accessible to any member of the audience with the necessary expertise in the field; Laplace used obvious (French
French language
French is a Romance language spoken as a first language in France, the Romandy region in Switzerland, Wallonia and Brussels in Belgium, Monaco, the regions of Quebec and Acadia in Canada, and by various communities elsewhere. Second-language speakers of French are distributed throughout many parts...
: évident).
diagram chasing: Given a commutative diagram
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
of objects and morphisms between them, if one wishes to prove some property of the morphisms (such as injectivity) which can be stated in terms of element
Element (category theory)
In category theory, the concept of an element, or a point, generalizes the more usual set theoretic concept of an element of a set to an object of any category. This idea often allows to restate definitions or properties of morphisms which are given by a universal property in more familiar terms...
s, then the proof can proceed by tracing the path of elements of various objects around the diagram as successive morphisms are applied to it. That is, one chases elements around the diagram, or does a diagram chase.
handwaving
Handwaving
Handwaving is a pejorative label applied to the action of displaying the appearance of doing something, when actually doing little, or nothing. For example, it is applied to debate techniques that involve logical fallacies. It is also used in working situations where productive work is expected,...
: A non-technique of proof mostly employed in lectures, where formal argument is not strictly necessary. It proceeds by omission of details or even significant ingredients, and is merely a plausibility argument.
: In a context not requiring rigor, this phrase often appears as a labor-saving device when the technical details of a complete argument would outweigh the conceptual benefits. The author gives a proof in a simple enough case that the computations are reasonable, and then indicates that "in general" the proof is similar.
morally true: Used to indicate that the speaker believes a statement should be true, given their mathematical experience, even though a proof has not yet been put forward. As a variation, the statement may in fact be false, but instead provide a slogan for or illustration of a correct principle. Hasse
Helmut Hasse
Helmut Hasse was a German mathematician working in algebraic number theory, known for fundamental contributions to class field theory, the application of p-adic numbers to local classfield theory and diophantine geometry , and to local zeta functions.-Life:He was born in Kassel, and died in...
's local-global principle is a particularly influential example of this.
trivial
Trivial (mathematics)
In mathematics, the adjective trivial is frequently used for objects that have a very simple structure...
: Similar to clearly. A concept is trivial if it holds by definition, is immediately corollary to a known statement, or is a simple special case of a more general concept.