Trivial (mathematics)
Encyclopedia
In mathematics
, the adjective trivial is frequently used for objects
(for examples, group
s or topological space
s) that have a very simple structure. The noun triviality usually refers to a simple technical aspect of some proof or definition.
Examples include:
Trivial also refers to solutions to an equation
that have a very simple structure, but for the sake of completeness cannot be omitted. These solutions are called the trivial solution. For example, consider the differential equation
where y = f(x) is a function
whose derivative
is y′. The trivial solution is
while a nontrivial solution is
Similarly, mathematicians often describe Fermat's Last Theorem
as asserting that there are no nontrivial integer solutions to the equation
when n is greater than 2. Clearly, there are some solutions to the equation. For example, 
is a solution for any n, as is a = 1, b = 0, c = 1. But such solutions are all obvious and uninteresting, and hence "trivial".
of a proof, which for the sake of completeness cannot be ignored. For instance, proofs by mathematical induction
have two parts: the "base case" that shows that the theorem is true for a particular initial value such as n = 0 or n = 1 and then an inductive step that shows that if the theorem is true for a certain value of n, it is also true for the value n + 1. The base case is often trivial and is identified as such, although there are cases where the base case is difficult but the inductive step is trivial. Similarly, one might want to prove that some property is possessed by all the members of a certain set. The main part of the proof will consider the case of a nonempty set, and examine the members in detail; in the case where the set is empty, the property is trivially possessed by all the members, since there are none. (See also Vacuous truth
.)
A common joke in the mathematical community is to say that "trivial" is synonymous with "proved" — that is, any theorem can be considered "trivial" once it is known to be true. Another joke concerns two mathematicians who are discussing a theorem; the first mathematician says that the theorem is "trivial". In response to the other's request for an explanation, he then proceeds with twenty minutes of exposition. At the end of the explanation, the second mathematician agrees that the theorem is trivial. These jokes point out the subjectivity of judgments about triviality. The joke also applies when the first mathematician says the theorem is trivial, but is unable to prove it himself. Often, as a joke, the theorem is then referred to as "intuitively obvious." Someone experienced in calculus
, for example, would consider the statement that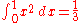
to be trivial. To a beginning student of calculus, though, this may not be obvious at all.
Note that triviality also depends on context. A proof in functional analysis
would probably, given a number, trivially assume the existence of a larger number. When proving basic results about the natural numbers in elementary number theory though, the proof may very well hinge on the remark that any natural number has a successor (which should then in itself be proved or taken as an axiom
, see Peano's axioms).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the adjective trivial is frequently used for objects
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
(for examples, group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s or topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s) that have a very simple structure. The noun triviality usually refers to a simple technical aspect of some proof or definition.
Trivial and non Trivial solutions
In mathematics, the term trivial is frequently used for objects (for examples, groups or topological spaces) that have a very simple structure. For non-mathematicians, they are sometimes more difficult to visualize or understand than other, more complicated objects.Examples include:
- empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
: the set containing no members - trivial groupTrivial groupIn mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
: the mathematical groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
containing only the identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them... - trivial ring: a ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
defined on a singleton set.
Trivial also refers to solutions to an equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
that have a very simple structure, but for the sake of completeness cannot be omitted. These solutions are called the trivial solution. For example, consider the differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
where y = f(x) is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
whose derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
is y′. The trivial solution is
- y = 0, the zero function
while a nontrivial solution is
- y (x) = ex, the exponential functionExponential functionIn mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
.
Similarly, mathematicians often describe Fermat's Last Theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
as asserting that there are no nontrivial integer solutions to the equation
when n is greater than 2. Clearly, there are some solutions to the equation. For example, is a solution for any n, as is a = 1, b = 0, c = 1. But such solutions are all obvious and uninteresting, and hence "trivial".Triviality in mathematical reasoning
Trivial may also refer to any easy caseProof by exhaustion
Proof by exhaustion, also known as proof by cases, perfect induction, or the brute force method, is a method of mathematical proof in which the statement to be proved is split into a finite number of cases and each case is checked to see if the proposition in question holds...
of a proof, which for the sake of completeness cannot be ignored. For instance, proofs by mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
have two parts: the "base case" that shows that the theorem is true for a particular initial value such as n = 0 or n = 1 and then an inductive step that shows that if the theorem is true for a certain value of n, it is also true for the value n + 1. The base case is often trivial and is identified as such, although there are cases where the base case is difficult but the inductive step is trivial. Similarly, one might want to prove that some property is possessed by all the members of a certain set. The main part of the proof will consider the case of a nonempty set, and examine the members in detail; in the case where the set is empty, the property is trivially possessed by all the members, since there are none. (See also Vacuous truth
Vacuous truth
A vacuous truth is a truth that is devoid of content because it asserts something about all members of a class that is empty or because it says "If A then B" when in fact A is inherently false. For example, the statement "all cell phones in the room are turned off" may be true...
.)
A common joke in the mathematical community is to say that "trivial" is synonymous with "proved" — that is, any theorem can be considered "trivial" once it is known to be true. Another joke concerns two mathematicians who are discussing a theorem; the first mathematician says that the theorem is "trivial". In response to the other's request for an explanation, he then proceeds with twenty minutes of exposition. At the end of the explanation, the second mathematician agrees that the theorem is trivial. These jokes point out the subjectivity of judgments about triviality. The joke also applies when the first mathematician says the theorem is trivial, but is unable to prove it himself. Often, as a joke, the theorem is then referred to as "intuitively obvious." Someone experienced in calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, for example, would consider the statement that
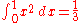
to be trivial. To a beginning student of calculus, though, this may not be obvious at all.
Note that triviality also depends on context. A proof in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
would probably, given a number, trivially assume the existence of a larger number. When proving basic results about the natural numbers in elementary number theory though, the proof may very well hinge on the remark that any natural number has a successor (which should then in itself be proved or taken as an axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
, see Peano's axioms).
See also
- DegeneracyDegeneracy (mathematics)In mathematics, a degenerate case is a limiting case in which a class of object changes its nature so as to belong to another, usually simpler, class....
- PathologicalPathological (mathematics)In mathematics, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive; the opposite is well-behaved....
- Parkinson's Law of Triviality
- Quantum trivialityQuantum trivialityIn a quantum field theory, charge screening can restrict the value of the observable "renormalized" charge of a classical theory. Ifthe only allowed value of the renormalized charge is zero, the theory is said to be "trivial" or noninteracting...
- Transformation
- TriviaTriviaThe trivia are the three lower Artes Liberales, i.e. grammar, rhetoric and logic. These were the topics of basic education, foundational to the quadrivia of higher education, and hence the material of basic education, of interest only to undergraduates...