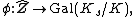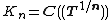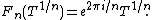Quasi-finite field
Encyclopedia
In mathematics
, a quasi-finite field is a generalisation of a finite field
. Standard local class field theory usually deals with complete valued fields whose residue field is finite (i.e. non-archimedean local fields), but the theory applies equally well when the residue field is only assumed quasi-finite.
K together with an isomorphism
of topological group
s
where Ks is an algebraic closure
of K (necessarily separable because K is perfect). The field extension
Ks/K is infinite, and the Galois group
is accordingly given the Krull topology. The group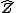
is the profinite completion of integer
s with respect to its subgroups of finite index.
This definition is equivalent to saying that K has a unique (necessarily cyclic) extension Kn of degree n for each integer n ≥ 1, and that the union of these extensions is equal to Ks. Moreover, as part of the structure of the quasi-finite field, there is a generator Fn for each Gal(Kn/K), and the generators must be coherent, in the sense that if n divides m, the restriction of Fm to Kn is equal to Fn.
Another example is K = C((T)), the ring of formal Laurent series in T over the field C of complex number
s. (These are simply formal power series
in which we also allow finitely many terms of negative degree.) Then K has a unique cyclic extension
of degree n for each n ≥ 1, whose union is an algebraic closure of K called the field of Puiseux series
, and that a generator of Gal(Kn/K) is given by
This construction works if C is replaced by any algebraically closed field C of characteristic zero.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a quasi-finite field is a generalisation of a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
. Standard local class field theory usually deals with complete valued fields whose residue field is finite (i.e. non-archimedean local fields), but the theory applies equally well when the residue field is only assumed quasi-finite.
Formal definition
A quasi-finite field is a perfect fieldPerfect field
In algebra, a field k is said to be perfect if any one of the following equivalent conditions holds:* Every irreducible polynomial over k has distinct roots.* Every polynomial over k is separable.* Every finite extension of k is separable...
K together with an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
of topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
s
where Ks is an algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of K (necessarily separable because K is perfect). The field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
Ks/K is infinite, and the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
is accordingly given the Krull topology. The group
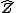is the profinite completion of integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s with respect to its subgroups of finite index.
This definition is equivalent to saying that K has a unique (necessarily cyclic) extension Kn of degree n for each integer n ≥ 1, and that the union of these extensions is equal to Ks. Moreover, as part of the structure of the quasi-finite field, there is a generator Fn for each Gal(Kn/K), and the generators must be coherent, in the sense that if n divides m, the restriction of Fm to Kn is equal to Fn.
Examples
The most basic example, which motivates the definition, is the finite field K = GF(q). It has a unique cyclic extension of degree n, namely Kn = GF(qn). The union of the Kn is the algebraic closure Ks. We take Fn to be the Frobenius element; that is, Fn(x) = xq.Another example is K = C((T)), the ring of formal Laurent series in T over the field C of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. (These are simply formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
in which we also allow finitely many terms of negative degree.) Then K has a unique cyclic extension
of degree n for each n ≥ 1, whose union is an algebraic closure of K called the field of Puiseux series
Puiseux series
In mathematics, Puiseux series are a generalization of formal power series, first introduced by Isaac Newton in 1676 and rediscovered by Victor Puiseux in 1850, that allows for negative and fractional exponents of the indeterminate...
, and that a generator of Gal(Kn/K) is given by
This construction works if C is replaced by any algebraically closed field C of characteristic zero.