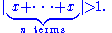Archimedean property
Encyclopedia
In abstract algebra
and analysis
, the Archimedean property, named after the ancient Greek mathematician Archimedes
of Syracuse
, is a property held by some ordered or normed groups, fields
, and other algebraic structure
s. Roughly speaking, it is the property of having no infinitely large or infinitely small elements. It was Otto Stolz
who gave the axiom of Archimedes its name because it appears as Axiom V of Archimedes 'The sphere and the cylinder'.
The notion arose from the theory of magnitudes
of Ancient Greece; it still plays an important role in modern mathematics such as David Hilbert
's axioms for geometry
, and the theories of ordered groups
, ordered field
s, and local fields.
An algebraic structure in which any two non-zero elements are comparable, in the sense that neither of them is infinitesimal
with respect to the other, is said to be Archimedean. A structure which has a pair of non-zero elements, one of which is infinitesimal with respect to the other, is said to be non-Archimedean. For example, a linearly ordered group
that is Archimedean is an Archimedean group
.
This can be made precise in various contexts with slightly different ways of formulation. For example, in the context of ordered field
s, one has the axiom of Archimedes which formulates this property, where the field of real number
s is Archimedean, but that of rational functions in real coefficients is not.
geometer and physicist Archimedes
of Syracuse
.
The Archimedean property appears in Book V of Euclid's Elements
as Definition 4:
Because Archimedes credited it to Eudoxus of Cnidus
it is also known as the "Theorem of Eudoxus" or the Eudoxus axiom.
Archimedes used infinitesimals in heuristic
arguments, although he denied that those were finished mathematical proof
s.
G. Then x is infinitesimal with respect to y (or equivalently, y is infinite with respect to x) if, for every natural number
n, the multiple nx is less than y, that is, the following inequality holds:
The group G is Archimedean if there is no pair x,y such that x is infinitesimal with respect to y.
Additionally, if K is an algebraic structure
with a unit (1) — for example, a ring
— a similar definition applies to K. If x is infinitesimal with respect to 1, then x is an infinitesimal element. Likewise, if y is infinite with respect to 1, then y is an infinite element. The algebraic structure K is Archimedean if it has no infinite elements and no infinitesimal elements.
has some additional nice properties.
In this setting, an ordered field K is Archimedean precisely when the following statement, called the axiom of Archimedes, holds:
Alternatively one can use the following characterization:
with each non-zero 
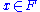and satisfies
and 
. Then, F is said to be Archimedean if for any non-zero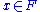 
there exists a natural number
n such that
Similarly, a normed space is Archimedean if a sum of
terms, each equal to a non-zero vector 
, has norm greater than one for sufficiently large 
. A field with an absolute value or a normed space is either Archimedean or satisfies the stronger condition, referred to as the ultrametric triangle inequality, 
or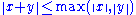 
, respectively. A field or normed space satisfying the ultrametric triangle inequality is called non-Archimedean.
The concept of a non-Archimedean normed linear space was introduced by A. F. Monna.
of the rational numbers, which themselves satisfy the axiom in both senses, with respect to an absolute value structure compatible with the ordering.
In the axiomatic theory of real numbers, the non-existence of nonzero infinitesimal real numbers is implied by the least upper bound property as follows. Denote by Z the set consisting of all positive infinitesimals. This set is bounded above by 1. Now assume by contradiction that Z is nonempty. Then it has a least upper bound c, which is also positive, so c/2 < c < 2c. Since c is an upper bound
of Z and 2c is strictly larger than c, 2c must be strictly larger than every positive infinitesimal. In particular, 2c cannot itself be an infinitesimal, for then 2c would have to be greater than itself. Moreover since c is the least upper bound of Z, c/2 must be infinitesimal. But 2c and c/2 cannot have different types by the above result, so there is a contradiction. The conclusion follows that Z is empty after all: there are no positive, infinitesimal real numbers.
One should note that the Archimedean property of real numbers holds also in constructive analysis, even though the least upper bound property may fail in that context.
, take the field of rational function
s with real coefficients. (A rational function is any function that can be expressed as one polynomial
divided by another polynomial; we will assume in what follows that this has been done in such a way that the leading coefficient of the denominator is positive.) To make this an ordered field, one must assign an ordering compatible with the addition and multiplication operations. Now f > g if and only if f − g > 0, so we only have to say which rational functions are considered positive. Call the function positive if the leading coefficient of the numerator is positive. (One must check that this ordering is well defined and compatible with addition and multiplication.) By this definition, the rational function 1/x is positive but less than the rational function 1. In fact, if n is any natural number, then n(1/x) = n/x is positive but still less than 1, no matter how big n is. Therefore, 1/x is an infinitesimal in this field.
This example generalizes to other coefficients. Taking rational functions with rational instead of real coefficients produces a countable non-Archimedean ordered field. Taking the coefficients to be the rational functions in a different variable, say y, produces an example with a different order type
.
fields which are the completions, do not have the Archimedean property as fields with absolute values. All Archimedean valued fields are isometrically isomorphic to a subfield of the complex numbers with a power of the usual absolute value. There is a non-trivial non-Archimedean valuation on every infinite field.
. The embedding of the rationals then gives a way of speaking about the rationals, integers, and natural numbers in K. The following are equivalent characterizations of Archimedean fields in terms of these substructures.
1. The natural numbers are cofinal
in K. That is, every element of K is less than some natural number. (This is not the case when there exist infinite elements.) Thus an Archimedean field is one whose natural numbers grow without bound.
2. Zero is the infimum
in K of the set {1/2, 1/3, 1/4, …}. (If K contained a positive infinitesimal it would be a lower bound for the set whence zero would not be the greatest lower bound.)
3. The set of elements of K between the positive and negative rationals is closed. This is because the set consists of all the infinitesimals, which is just the closed set {0} when there are no nonzero infinitesimals, and otherwise is open, there being neither a least nor greatest nonzero infinitesimal. In the latter case, (i) every infinitesimal is less than every positive rational, (ii) there is neither a greatest infinitesimal nor a least positive rational, and (iii) there is nothing else in between, a situation that points up both the incompleteness and disconnectedness of any non-Archimedean field.
4. For any x in K the set of integers greater than x has a least element. (If x were a negative infinite quantity every integer would be greater than it.)
5. Every nonempty open interval of K contains a rational. (If x is a positive infinitesimal, the open interval (x,2x) contains infinitely many infinitesimals but not a single rational.)
6. The rationals are dense
in K with respect to both sup and inf. (That is, every element of K is the sup of some set of rationals, and the inf of some other set of rationals.) Thus an Archimedean field is any dense ordered extension of the rationals, in the sense of any ordered field that densely embeds its rational elements.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and analysis
Analysis
Analysis is the process of breaking a complex topic or substance into smaller parts to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle , though analysis as a formal concept is a relatively recent development.The word is...
, the Archimedean property, named after the ancient Greek mathematician Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
of Syracuse
Syracuse, Italy
Syracuse is a historic city in Sicily, the capital of the province of Syracuse. The city is notable for its rich Greek history, culture, amphitheatres, architecture, and as the birthplace of the preeminent mathematician and engineer Archimedes. This 2,700-year-old city played a key role in...
, is a property held by some ordered or normed groups, fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, and other algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s. Roughly speaking, it is the property of having no infinitely large or infinitely small elements. It was Otto Stolz
Otto Stolz
Otto Stolz was an Austrian mathematician noted for his work on mathematical analysis and infinitesimals. Born in Hall in Tirol, he studied in Innsbruck from 1860 and in Vienna from 1863, receiving his habilitation there in 1867...
who gave the axiom of Archimedes its name because it appears as Axiom V of Archimedes 'The sphere and the cylinder'.
The notion arose from the theory of magnitudes
Magnitude (mathematics)
The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
of Ancient Greece; it still plays an important role in modern mathematics such as David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
's axioms for geometry
Hilbert's axioms
Hilbert's axioms are a set of 20 assumptions proposed by David Hilbert in 1899 in his book Grundlagen der Geometrie , as the foundation for a modern treatment of Euclidean geometry...
, and the theories of ordered groups
Linearly ordered group
In abstract algebra a linearly ordered or totally ordered group is an ordered group G such that the order relation "≤" is total...
, ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
s, and local fields.
An algebraic structure in which any two non-zero elements are comparable, in the sense that neither of them is infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
with respect to the other, is said to be Archimedean. A structure which has a pair of non-zero elements, one of which is infinitesimal with respect to the other, is said to be non-Archimedean. For example, a linearly ordered group
Linearly ordered group
In abstract algebra a linearly ordered or totally ordered group is an ordered group G such that the order relation "≤" is total...
that is Archimedean is an Archimedean group
Archimedean group
In abstract algebra, a branch of mathematics, an Archimedean group is an algebraic structure consisting of a set together with a binary operation and binary relation satisfying certain axioms detailed below. We can also say that an Archimedean group is a linearly ordered group for which the...
.
This can be made precise in various contexts with slightly different ways of formulation. For example, in the context of ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
s, one has the axiom of Archimedes which formulates this property, where the field of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s is Archimedean, but that of rational functions in real coefficients is not.
History and origin of the name of the Archimedean property
The concept is named after the ancient GreekAncient Greece
Ancient Greece is a civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity. Immediately following this period was the beginning of the Early Middle Ages and the Byzantine era. Included in Ancient Greece is the...
geometer and physicist Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
of Syracuse
Syracuse, Italy
Syracuse is a historic city in Sicily, the capital of the province of Syracuse. The city is notable for its rich Greek history, culture, amphitheatres, architecture, and as the birthplace of the preeminent mathematician and engineer Archimedes. This 2,700-year-old city played a key role in...
.
The Archimedean property appears in Book V of Euclid's Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
as Definition 4:
Because Archimedes credited it to Eudoxus of Cnidus
Eudoxus of Cnidus
Eudoxus of Cnidus was a Greek astronomer, mathematician, scholar and student of Plato. Since all his own works are lost, our knowledge of him is obtained from secondary sources, such as Aratus's poem on astronomy...
it is also known as the "Theorem of Eudoxus" or the Eudoxus axiom.
Archimedes used infinitesimals in heuristic
Heuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
arguments, although he denied that those were finished mathematical proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
s.
Definition for linearly ordered groups
Let x and y be positive elements of a linearly ordered groupLinearly ordered group
In abstract algebra a linearly ordered or totally ordered group is an ordered group G such that the order relation "≤" is total...
G. Then x is infinitesimal with respect to y (or equivalently, y is infinite with respect to x) if, for every natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n, the multiple nx is less than y, that is, the following inequality holds:
The group G is Archimedean if there is no pair x,y such that x is infinitesimal with respect to y.
Additionally, if K is an algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
with a unit (1) — for example, a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
— a similar definition applies to K. If x is infinitesimal with respect to 1, then x is an infinitesimal element. Likewise, if y is infinite with respect to 1, then y is an infinite element. The algebraic structure K is Archimedean if it has no infinite elements and no infinitesimal elements.
Ordered fields
An ordered fieldOrdered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
has some additional nice properties.
- One may assume that the rational numbers are contained in the field.
- If x is infinitesimal, then 1/x is infinite, and vice versa. Therefore to verify that a field is Archimedean it is enough to check only that there are no infinitesimal elements, or to check that there are no infinite elements.
- If x is infinitesimal and r is a rational number, then rx is also infinitesimal. As a result, given a general element c, the three numbers c/2, c, and 2c are either all infinitesimal or all non-infinitesimal.
In this setting, an ordered field K is Archimedean precisely when the following statement, called the axiom of Archimedes, holds:
- Let x be any element of K. Then there exists a natural number n such that n > x.
Alternatively one can use the following characterization:
- For any positive ε in K, there exists a natural number n, such that 1/n < ε.
Definition for normed fields
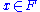The qualifier "Archimedean" is also formulated in the theory of rank one valued fields and normed spaces over rank one valued fields as follows. Let F be a field endowed with an absolute value function, i.e., a function which associates the real number 0 with the field element 0 and associates a positive real number with each non-zero and satisfies and . Then, F is said to be Archimedean if for any non-zero 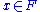there exists a natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n such that
Similarly, a normed space is Archimedean if a sum of
terms, each equal to a non-zero vector , has norm greater than one for sufficiently large . A field with an absolute value or a normed space is either Archimedean or satisfies the stronger condition, referred to as the ultrametric triangle inequality, or 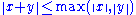, respectively. A field or normed space satisfying the ultrametric triangle inequality is called non-Archimedean.The concept of a non-Archimedean normed linear space was introduced by A. F. Monna.
Archimedean property of the real numbers
The field of the real numbers is Archimedean both as an ordered field and as a normed field. It is chiefly because the real numbers are obtained as the completionComplete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
of the rational numbers, which themselves satisfy the axiom in both senses, with respect to an absolute value structure compatible with the ordering.
In the axiomatic theory of real numbers, the non-existence of nonzero infinitesimal real numbers is implied by the least upper bound property as follows. Denote by Z the set consisting of all positive infinitesimals. This set is bounded above by 1. Now assume by contradiction that Z is nonempty. Then it has a least upper bound c, which is also positive, so c/2 < c < 2c. Since c is an upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
of Z and 2c is strictly larger than c, 2c must be strictly larger than every positive infinitesimal. In particular, 2c cannot itself be an infinitesimal, for then 2c would have to be greater than itself. Moreover since c is the least upper bound of Z, c/2 must be infinitesimal. But 2c and c/2 cannot have different types by the above result, so there is a contradiction. The conclusion follows that Z is empty after all: there are no positive, infinitesimal real numbers.
One should note that the Archimedean property of real numbers holds also in constructive analysis, even though the least upper bound property may fail in that context.
Non-Archimedean ordered field
For an example of an ordered field that is not ArchimedeanNon-Archimedean ordered field
In mathematics, a non-Archimedean ordered field is an ordered field that does not satisfy the Archimedean property. Examples are the Levi-Civita field, the hyperreal numbers, the surreal numbers, the Dehn field, and the field of rational functions with real coefficients with a suitable...
, take the field of rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s with real coefficients. (A rational function is any function that can be expressed as one polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
divided by another polynomial; we will assume in what follows that this has been done in such a way that the leading coefficient of the denominator is positive.) To make this an ordered field, one must assign an ordering compatible with the addition and multiplication operations. Now f > g if and only if f − g > 0, so we only have to say which rational functions are considered positive. Call the function positive if the leading coefficient of the numerator is positive. (One must check that this ordering is well defined and compatible with addition and multiplication.) By this definition, the rational function 1/x is positive but less than the rational function 1. In fact, if n is any natural number, then n(1/x) = n/x is positive but still less than 1, no matter how big n is. Therefore, 1/x is an infinitesimal in this field.
This example generalizes to other coefficients. Taking rational functions with rational instead of real coefficients produces a countable non-Archimedean ordered field. Taking the coefficients to be the rational functions in a different variable, say y, produces an example with a different order type
Order type
In mathematics, especially in set theory, two ordered sets X,Y are said to have the same order type just when they are order isomorphic, that is, when there exists a bijection f: X → Y such that both f and its inverse are monotone...
.
Non-Archimedean valued fields
The field of the rational numbers endowed with the p-adic metric and the p-adic numberP-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
fields which are the completions, do not have the Archimedean property as fields with absolute values. All Archimedean valued fields are isometrically isomorphic to a subfield of the complex numbers with a power of the usual absolute value. There is a non-trivial non-Archimedean valuation on every infinite field.
Equivalent definitions of Archimedean ordered field
Every linearly ordered field K contains (an isomorphic copy of) the rationals as an ordered subfield, namely the subfield generated by the multiplicative unit 1 of K, which in turn contains the integers as an ordered subgroup, which contains the natural numbers as an ordered monoidMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
. The embedding of the rationals then gives a way of speaking about the rationals, integers, and natural numbers in K. The following are equivalent characterizations of Archimedean fields in terms of these substructures.
1. The natural numbers are cofinal
Cofinal (mathematics)
In mathematics, let A be a set and let ≤ be a binary relation on A. Then a subset B of A is said to be cofinal if it satisfies the following condition:This definition is most commonly applied when A is a partially ordered set or directed set under the relation ≤. Also, the notion of cofinal...
in K. That is, every element of K is less than some natural number. (This is not the case when there exist infinite elements.) Thus an Archimedean field is one whose natural numbers grow without bound.
2. Zero is the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
in K of the set {1/2, 1/3, 1/4, …}. (If K contained a positive infinitesimal it would be a lower bound for the set whence zero would not be the greatest lower bound.)
3. The set of elements of K between the positive and negative rationals is closed. This is because the set consists of all the infinitesimals, which is just the closed set {0} when there are no nonzero infinitesimals, and otherwise is open, there being neither a least nor greatest nonzero infinitesimal. In the latter case, (i) every infinitesimal is less than every positive rational, (ii) there is neither a greatest infinitesimal nor a least positive rational, and (iii) there is nothing else in between, a situation that points up both the incompleteness and disconnectedness of any non-Archimedean field.
4. For any x in K the set of integers greater than x has a least element. (If x were a negative infinite quantity every integer would be greater than it.)
5. Every nonempty open interval of K contains a rational. (If x is a positive infinitesimal, the open interval (x,2x) contains infinitely many infinitesimals but not a single rational.)
6. The rationals are dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
in K with respect to both sup and inf. (That is, every element of K is the sup of some set of rationals, and the inf of some other set of rationals.) Thus an Archimedean field is any dense ordered extension of the rationals, in the sense of any ordered field that densely embeds its rational elements.