
Homology theory
Encyclopedia
In mathematics
, homology theory is the axiom
atic study of the intuitive geometric idea of homology of cycles on topological space
s. It can be broadly defined as the study of homology
theories on topological spaces.
 To any topological space
To any topological space
 and any natural number
and any natural number  , one can associate a set
, one can associate a set  , whose elements are called (
, whose elements are called ( -dimensional) homology classes. There is a well-defined way to add and subtract homology classes, which makes
-dimensional) homology classes. There is a well-defined way to add and subtract homology classes, which makes  into an abelian group
into an abelian group
, called the th homology group of
th homology group of  . In heuristic terms, the size and structure of
. In heuristic terms, the size and structure of  gives information about the number of
gives information about the number of  -dimensional holes in
-dimensional holes in  . For example, if
. For example, if  is a figure eight, then it has two holes, which in this context count as being one-dimensional. The corresponding homology group
is a figure eight, then it has two holes, which in this context count as being one-dimensional. The corresponding homology group  can be identified with the group
can be identified with the group  of pairs of integers, with one copy of
of pairs of integers, with one copy of  for each hole. While it seems very straightforward to say that
for each hole. While it seems very straightforward to say that  has two holes, it is surprisingly hard to formulate this in a mathematically rigorous way; this is a central purpose of homology theory.
has two holes, it is surprisingly hard to formulate this in a mathematically rigorous way; this is a central purpose of homology theory.
For a more intricate example, if is a Klein bottle
is a Klein bottle
then can be identified with
can be identified with  . This is not just a sum of copies of
. This is not just a sum of copies of  , so it gives more subtle information than just a count of holes.
, so it gives more subtle information than just a count of holes.
The formal definition of can be sketched as follows. The elements of
can be sketched as follows. The elements of  are one-dimensional cycles, except that two cycles are considered to represent the same element if they are homologous. The simplest kind of one-dimensional cycles are just closed curves in
are one-dimensional cycles, except that two cycles are considered to represent the same element if they are homologous. The simplest kind of one-dimensional cycles are just closed curves in  , which could consist of one or more loops. If a closed curve
, which could consist of one or more loops. If a closed curve  can be deformed continuously within
can be deformed continuously within  to another closed curve
to another closed curve  , then
, then  and
and  are homologous and so determine the same element of
are homologous and so determine the same element of  . This captures the main geometric idea, but the full definition is somewhat more complex. For details, see singular homology
. This captures the main geometric idea, but the full definition is somewhat more complex. For details, see singular homology
. There is also a version (called simplicial homology
) that works when is presented as a simplicial complex
is presented as a simplicial complex
; this is smaller and easier to understand, but technically less flexible.
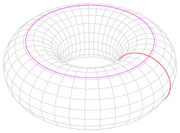
For example, let be a torus, as shown on the right.
be a torus, as shown on the right.
Let be the pink curve, and let
be the pink curve, and let  be the red one. For integers
be the red one. For integers  and
and  , we have another closed curve that goes
, we have another closed curve that goes  times around
times around  and then
and then  times around
times around  ; this is denoted by
; this is denoted by  . It can be shown that any closed curve in
. It can be shown that any closed curve in  is homologous to
is homologous to  for some
for some  and
and  , and thus that
, and thus that  is again isomorphic to
is again isomorphic to  .
.
 , one can define cohomology groups
, one can define cohomology groups  . In the common case where each group
. In the common case where each group  is isomorphic to
is isomorphic to  for some
for some  , we just have
, we just have  , which is again isomorphic to
, which is again isomorphic to  , and
, and  , so
, so  and
and  determine each other. In general, the relationship between
determine each other. In general, the relationship between  and
and  is only a little more complicated, and is controlled by the universal coefficient theorem
is only a little more complicated, and is controlled by the universal coefficient theorem
. The main advantage of cohomology over homology is that it has a natural ring structure: there is a way to multiply an -dimensional cohomology class by a
-dimensional cohomology class by a  -dimensional cohomology class to get an
-dimensional cohomology class to get an  -dimensional cohomology class.
-dimensional cohomology class.
 be a compact
be a compact
oriented
manifold
of dimension . The Poincaré duality
. The Poincaré duality
theorem gives a natural isomorphism , which we can use to transfer the ring structure from cohomology to homology. For any compact oriented submanifold
, which we can use to transfer the ring structure from cohomology to homology. For any compact oriented submanifold  of dimension
of dimension  , one can define a so-called fundamental class
, one can define a so-called fundamental class  . If
. If  is another compact oriented submanifold which meets
is another compact oriented submanifold which meets  transversely
transversely
, it works out that . In many cases the group
. In many cases the group  will have a basis consisting of fundamental classes of submanifolds, in which case the product rule
will have a basis consisting of fundamental classes of submanifolds, in which case the product rule  gives a very clear geometric picture of the ring structure.
gives a very clear geometric picture of the ring structure.
 is an open subset of the complex plane
is an open subset of the complex plane
, that is a holomorphic function on
is a holomorphic function on  , and that
, and that  is a closed curve in
is a closed curve in  . There is then a standard way to define the contour integral
. There is then a standard way to define the contour integral  , which is a central idea in complex analysis
, which is a central idea in complex analysis
. One formulation of Cauchy's integral theorem
is as follows: if and
and  are homologous, then
are homologous, then  . (Many authors consider only the case where
. (Many authors consider only the case where  is simply connected, in which case every closed curve is homologous to the empty curve and so
is simply connected, in which case every closed curve is homologous to the empty curve and so  .) This means that we can make sense of
.) This means that we can make sense of  when
when  is merely a homology class, or in other words an element of
is merely a homology class, or in other words an element of  . It is also important that in the case where
. It is also important that in the case where  is the derivative of another function
is the derivative of another function  , we always have
, we always have  (even when
(even when  is not homologous to zero).
is not homologous to zero).
This is the simplest case of a much more general relationship between homology and integration, which is most efficiently formulated in terms of differential forms and de Rham cohomology
. To explain this briefly, suppose that is an open subset of
is an open subset of  , or more generally, that
, or more generally, that  is a manifold
is a manifold
. One can then define objects called -forms on
-forms on  . If
. If  is open in
is open in  , then the 0-forms are just the scalar fields, the 1-forms are the vector fields, the 2-forms are the same as the 1-forms, and the 3-forms are the same as the 0-forms. There is also a kind of differentiation operation called the exterior derivative
, then the 0-forms are just the scalar fields, the 1-forms are the vector fields, the 2-forms are the same as the 1-forms, and the 3-forms are the same as the 0-forms. There is also a kind of differentiation operation called the exterior derivative
: if is an
is an  -form, then the exterior derivative is an
-form, then the exterior derivative is an  -form denoted by
-form denoted by  . The standard operators div
. The standard operators div
, grad
and curl from vector calculus can be seen as special cases of this. There is a procedure for integrating an -form
-form  over an
over an  -cycle
-cycle  to get a number
to get a number  . It can be shown that
. It can be shown that  for any
for any  -form
-form  , and that
, and that  depends only on the homology class of
depends only on the homology class of  , provided that
, provided that  . The classical Stokes's Theorem and Divergence Theorem
. The classical Stokes's Theorem and Divergence Theorem
can be seen as special cases of this.
We say that is closed if
is closed if  , and exact if
, and exact if  for some
for some  . It can be shown that
. It can be shown that  is always zero, so that exact forms are always closed. The de Rham cohomology
is always zero, so that exact forms are always closed. The de Rham cohomology
group is the quotient of the group of closed forms by the subgroup of exact forms. It follows from the above that there is a well-defined pairing
is the quotient of the group of closed forms by the subgroup of exact forms. It follows from the above that there is a well-defined pairing  given by integration.
given by integration.
, Alexander–Spanier cohomology or Sheaf cohomology
). These give different answers for some exotic spaces, but there is a large class of spaces on which they all agree. This is most easily understood axiomatically: there is a list of properties known as the Eilenberg–Steenrod axioms, and any two constructions that share those properties will agree at least on all finite CW complex
es, for example.
One of the axioms is the so-called dimension axiom: if is a single point, then
is a single point, then  for all
for all  , and
, and  . We can generalise slightly by allowing an arbitrary abelian group
. We can generalise slightly by allowing an arbitrary abelian group  in dimension zero, but still insisting that the groups in nonzero dimension are trivial. It turns out that there is again an essentially unique system of groups satisfying these axioms, which are denoted by
in dimension zero, but still insisting that the groups in nonzero dimension are trivial. It turns out that there is again an essentially unique system of groups satisfying these axioms, which are denoted by  . In the common case where each group
. In the common case where each group  is isomorphic to
is isomorphic to  for some
for some  , we just have
, we just have  . In general, the relationship between
. In general, the relationship between  and
and  is only a little more complicated, and is again controlled by the Universal coefficient theorem
is only a little more complicated, and is again controlled by the Universal coefficient theorem
.
More significantly, we can drop the dimension axiom altogether. There are a number of different ways to define groups satisfying all the other axioms, including the following:
These are called generalised homology theories; they carry much richer information than ordinary homology, but are often harder to compute. Their study is tightly linked (via the Brown representability theorem) to stable homotopy.
consists of groups (for all
(for all  ) and homomorphisms
) and homomorphisms  satisfying
satisfying  . This condition shows that the groups
. This condition shows that the groups  are contained in the groups
are contained in the groups  , so one can form the quotient groups
, so one can form the quotient groups  , which are called the homology groups of the original complex. There is a similar theory of cochain complexes, consisting of groups
, which are called the homology groups of the original complex. There is a similar theory of cochain complexes, consisting of groups  and homomorphisms
and homomorphisms  . The simplicial, singular, Čech and Alexander–Spanier groups are all defined by first constructing a chain complex or cochain complex, and then taking its homology. Thus, a substantial part of the work in setting up these groups involves the general theory of chain and cochain complexes, which is known as homological algebra.
. The simplicial, singular, Čech and Alexander–Spanier groups are all defined by first constructing a chain complex or cochain complex, and then taking its homology. Thus, a substantial part of the work in setting up these groups involves the general theory of chain and cochain complexes, which is known as homological algebra.
One can also associate (co)chain complexes to a wide variety of other mathematical objects, and then take their (co)homology. For example, there are cohomology modules for groups, Lie algebras and so on.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, homology theory is the axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
atic study of the intuitive geometric idea of homology of cycles on topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s. It can be broadly defined as the study of homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
theories on topological spaces.
The general idea

Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
 and any natural number
and any natural number  , one can associate a set
, one can associate a set  , whose elements are called (
, whose elements are called ( -dimensional) homology classes. There is a well-defined way to add and subtract homology classes, which makes
-dimensional) homology classes. There is a well-defined way to add and subtract homology classes, which makes  into an abelian group
into an abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, called the
 th homology group of
th homology group of  . In heuristic terms, the size and structure of
. In heuristic terms, the size and structure of  gives information about the number of
gives information about the number of  -dimensional holes in
-dimensional holes in  . For example, if
. For example, if  is a figure eight, then it has two holes, which in this context count as being one-dimensional. The corresponding homology group
is a figure eight, then it has two holes, which in this context count as being one-dimensional. The corresponding homology group  can be identified with the group
can be identified with the group  of pairs of integers, with one copy of
of pairs of integers, with one copy of  for each hole. While it seems very straightforward to say that
for each hole. While it seems very straightforward to say that  has two holes, it is surprisingly hard to formulate this in a mathematically rigorous way; this is a central purpose of homology theory.
has two holes, it is surprisingly hard to formulate this in a mathematically rigorous way; this is a central purpose of homology theory.For a more intricate example, if
 is a Klein bottle
is a Klein bottleKlein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
then
 can be identified with
can be identified with  . This is not just a sum of copies of
. This is not just a sum of copies of  , so it gives more subtle information than just a count of holes.
, so it gives more subtle information than just a count of holes.The formal definition of
 can be sketched as follows. The elements of
can be sketched as follows. The elements of  are one-dimensional cycles, except that two cycles are considered to represent the same element if they are homologous. The simplest kind of one-dimensional cycles are just closed curves in
are one-dimensional cycles, except that two cycles are considered to represent the same element if they are homologous. The simplest kind of one-dimensional cycles are just closed curves in  , which could consist of one or more loops. If a closed curve
, which could consist of one or more loops. If a closed curve  can be deformed continuously within
can be deformed continuously within  to another closed curve
to another closed curve  , then
, then  and
and  are homologous and so determine the same element of
are homologous and so determine the same element of  . This captures the main geometric idea, but the full definition is somewhat more complex. For details, see singular homology
. This captures the main geometric idea, but the full definition is somewhat more complex. For details, see singular homologySingular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
. There is also a version (called simplicial homology
Simplicial homology
In mathematics, in the area of algebraic topology, simplicial homology is a theory with a finitary definition, and is probably the most tangible variant of homology theory....
) that works when
 is presented as a simplicial complex
is presented as a simplicial complexSimplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
; this is smaller and easier to understand, but technically less flexible.
For example, let
 be a torus, as shown on the right.
be a torus, as shown on the right.Let
 be the pink curve, and let
be the pink curve, and let  be the red one. For integers
be the red one. For integers  and
and  , we have another closed curve that goes
, we have another closed curve that goes  times around
times around  and then
and then  times around
times around  ; this is denoted by
; this is denoted by  . It can be shown that any closed curve in
. It can be shown that any closed curve in  is homologous to
is homologous to  for some
for some  and
and  , and thus that
, and thus that  is again isomorphic to
is again isomorphic to  .
.Cohomology
As well as the homology groups , one can define cohomology groups
, one can define cohomology groups  . In the common case where each group
. In the common case where each group  is isomorphic to
is isomorphic to  for some
for some  , we just have
, we just have  , which is again isomorphic to
, which is again isomorphic to  , and
, and  , so
, so  and
and  determine each other. In general, the relationship between
determine each other. In general, the relationship between  and
and  is only a little more complicated, and is controlled by the universal coefficient theorem
is only a little more complicated, and is controlled by the universal coefficient theoremUniversal coefficient theorem
In mathematics, the universal coefficient theorem in algebraic topology establishes the relationship in homology theory between the integral homology of a topological space X, and its homology with coefficients in any abelian group A...
. The main advantage of cohomology over homology is that it has a natural ring structure: there is a way to multiply an
 -dimensional cohomology class by a
-dimensional cohomology class by a  -dimensional cohomology class to get an
-dimensional cohomology class to get an  -dimensional cohomology class.
-dimensional cohomology class.Applications
Notable theorems proved using homology include the following:- The Brouwer fixed point theoremBrouwer fixed point theoremBrouwer's fixed-point theorem is a fixed-point theorem in topology, named after Luitzen Brouwer. It states that for any continuous function f with certain properties there is a point x0 such that f = x0. The simplest form of Brouwer's theorem is for continuous functions f from a disk D to...
: If is any continuous map from the ball
is any continuous map from the ball  to itself, then there is a fixed point
to itself, then there is a fixed point  with
with  .
. - Invariance of domainInvariance of domainInvariance of domain is a theorem in topology about homeomorphic subsets of Euclidean space Rn. It states:The theorem and its proof are due to L.E.J. Brouwer, published in 1912...
: If U is an open subsetOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of and
and  is an injective continuous map, then
is an injective continuous map, then  is open and
is open and  is a homeomorphismHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
is a homeomorphismHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
between and
and  .
. - The Hairy ball theoremHairy ball theoremThe hairy ball theorem of algebraic topology states that there is no nonvanishing continuous tangent vector field on an even-dimensional n-sphere. An ordinary sphere is a 2-sphere, so that this theorem will hold for an ordinary sphere...
: any vector field on the 2-sphere (or more generally, the -sphere for any
-sphere for any  ) vanishes at some point.
) vanishes at some point. - The Borsuk–Ulam theoremBorsuk–Ulam theoremIn mathematics, the Borsuk–Ulam theorem, named after Stanisław Ulam and Karol Borsuk, states that every continuous function from an n-sphere into Euclidean n-space maps some pair of antipodal points to the same point....
: any continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
from an n-sphere into Euclidean n-spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
maps some pair of antipodal pointAntipodal pointIn mathematics, the antipodal point of a point on the surface of a sphere is the point which is diametrically opposite to it — so situated that a line drawn from the one to the other passes through the centre of the sphere and forms a true diameter....
s to the same point. (Two points on a sphere are called antipodal if they are in exactly opposite directions from the sphere's center.)
Intersection theory and Poincaré duality
Let be a compact
be a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
oriented
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
of dimension
 . The Poincaré duality
. The Poincaré dualityPoincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
theorem gives a natural isomorphism
 , which we can use to transfer the ring structure from cohomology to homology. For any compact oriented submanifold
, which we can use to transfer the ring structure from cohomology to homology. For any compact oriented submanifold  of dimension
of dimension  , one can define a so-called fundamental class
, one can define a so-called fundamental class  . If
. If  is another compact oriented submanifold which meets
is another compact oriented submanifold which meets  transversely
transverselyTransversality
In mathematics, transversality is a notion that describes how spaces can intersect; transversality can be seen as the "opposite" of tangency, and plays a role in general position. It formalizes the idea of a generic intersection in differential topology...
, it works out that
 . In many cases the group
. In many cases the group  will have a basis consisting of fundamental classes of submanifolds, in which case the product rule
will have a basis consisting of fundamental classes of submanifolds, in which case the product rule  gives a very clear geometric picture of the ring structure.
gives a very clear geometric picture of the ring structure.Connection with integration
Suppose that is an open subset of the complex plane
is an open subset of the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, that
 is a holomorphic function on
is a holomorphic function on  , and that
, and that  is a closed curve in
is a closed curve in  . There is then a standard way to define the contour integral
. There is then a standard way to define the contour integral  , which is a central idea in complex analysis
, which is a central idea in complex analysisComplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
. One formulation of Cauchy's integral theorem
Cauchy's integral theorem
In mathematics, the Cauchy integral theorem in complex analysis, named after Augustin-Louis Cauchy, is an important statement about line integrals for holomorphic functions in the complex plane...
is as follows: if
 and
and  are homologous, then
are homologous, then  . (Many authors consider only the case where
. (Many authors consider only the case where  is simply connected, in which case every closed curve is homologous to the empty curve and so
is simply connected, in which case every closed curve is homologous to the empty curve and so  .) This means that we can make sense of
.) This means that we can make sense of  when
when  is merely a homology class, or in other words an element of
is merely a homology class, or in other words an element of  . It is also important that in the case where
. It is also important that in the case where  is the derivative of another function
is the derivative of another function  , we always have
, we always have  (even when
(even when  is not homologous to zero).
is not homologous to zero).This is the simplest case of a much more general relationship between homology and integration, which is most efficiently formulated in terms of differential forms and de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
. To explain this briefly, suppose that
 is an open subset of
is an open subset of  , or more generally, that
, or more generally, that  is a manifold
is a manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
. One can then define objects called
 -forms on
-forms on  . If
. If  is open in
is open in  , then the 0-forms are just the scalar fields, the 1-forms are the vector fields, the 2-forms are the same as the 1-forms, and the 3-forms are the same as the 0-forms. There is also a kind of differentiation operation called the exterior derivative
, then the 0-forms are just the scalar fields, the 1-forms are the vector fields, the 2-forms are the same as the 1-forms, and the 3-forms are the same as the 0-forms. There is also a kind of differentiation operation called the exterior derivativeExterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
: if
 is an
is an  -form, then the exterior derivative is an
-form, then the exterior derivative is an  -form denoted by
-form denoted by  . The standard operators div
. The standard operators divDivergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
, grad
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
and curl from vector calculus can be seen as special cases of this. There is a procedure for integrating an
 -form
-form  over an
over an  -cycle
-cycle  to get a number
to get a number  . It can be shown that
. It can be shown that  for any
for any  -form
-form  , and that
, and that  depends only on the homology class of
depends only on the homology class of  , provided that
, provided that  . The classical Stokes's Theorem and Divergence Theorem
. The classical Stokes's Theorem and Divergence TheoremDivergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
can be seen as special cases of this.
We say that
 is closed if
is closed if  , and exact if
, and exact if  for some
for some  . It can be shown that
. It can be shown that  is always zero, so that exact forms are always closed. The de Rham cohomology
is always zero, so that exact forms are always closed. The de Rham cohomologyDe Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
group
 is the quotient of the group of closed forms by the subgroup of exact forms. It follows from the above that there is a well-defined pairing
is the quotient of the group of closed forms by the subgroup of exact forms. It follows from the above that there is a well-defined pairing  given by integration.
given by integration.Axiomatics and generalised homology
There are various ways to define cohomology groups (for example singular cohomology, Čech cohomologyCech cohomology
In mathematics, specifically algebraic topology, Čech cohomology is a cohomology theory based on the intersection properties of open covers of a topological space. It is named for the mathematician Eduard Čech.-Motivation:...
, Alexander–Spanier cohomology or Sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
). These give different answers for some exotic spaces, but there is a large class of spaces on which they all agree. This is most easily understood axiomatically: there is a list of properties known as the Eilenberg–Steenrod axioms, and any two constructions that share those properties will agree at least on all finite CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
es, for example.
One of the axioms is the so-called dimension axiom: if
 is a single point, then
is a single point, then  for all
for all  , and
, and  . We can generalise slightly by allowing an arbitrary abelian group
. We can generalise slightly by allowing an arbitrary abelian group  in dimension zero, but still insisting that the groups in nonzero dimension are trivial. It turns out that there is again an essentially unique system of groups satisfying these axioms, which are denoted by
in dimension zero, but still insisting that the groups in nonzero dimension are trivial. It turns out that there is again an essentially unique system of groups satisfying these axioms, which are denoted by  . In the common case where each group
. In the common case where each group  is isomorphic to
is isomorphic to  for some
for some  , we just have
, we just have  . In general, the relationship between
. In general, the relationship between  and
and  is only a little more complicated, and is again controlled by the Universal coefficient theorem
is only a little more complicated, and is again controlled by the Universal coefficient theoremUniversal coefficient theorem
In mathematics, the universal coefficient theorem in algebraic topology establishes the relationship in homology theory between the integral homology of a topological space X, and its homology with coefficients in any abelian group A...
.
More significantly, we can drop the dimension axiom altogether. There are a number of different ways to define groups satisfying all the other axioms, including the following:
- The stable homotopy groupsStable homotopy theoryIn mathematics, stable homotopy theory is that part of homotopy theory concerned with all structure and phenomena that remain after sufficiently many applications of the suspension functor...

- Various different flavours of cobordismCobordismIn mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
groups: ,
,  ,
,  and so on. The last of these (known as complex cobordismComplex cobordismIn mathematics, complex cobordism is a generalized cohomology theory related to cobordism of manifolds. Its spectrum is denoted by MU. It is an exceptionally powerful cohomology theory, but can be quite hard to compute, so often instead of using it directly one uses some slightly weaker theories...
and so on. The last of these (known as complex cobordismComplex cobordismIn mathematics, complex cobordism is a generalized cohomology theory related to cobordism of manifolds. Its spectrum is denoted by MU. It is an exceptionally powerful cohomology theory, but can be quite hard to compute, so often instead of using it directly one uses some slightly weaker theories...
) is especially important, because of the link with formal group theoryFormal groupIn mathematics, a formal group law is a formal power series behaving as if it were the product of a Lie group. They were introduced by . The term formal group sometimes means the same as formal group law, and sometimes means one of several generalizations. Formal groups are intermediate between...
via a theorem of Daniel Quillen. - Various different flavours of K-theoryK-theoryIn mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
: (real periodic K-theory),
(real periodic K-theory),  (real connective),
(real connective),  (complex periodic),
(complex periodic),  (complex connective) and so on.
(complex connective) and so on. - Brown–Peterson homologyBrown–Peterson cohomologyIn mathematics, Brown–Peterson cohomology is a generalized cohomology theory introduced by, depending on a choice of prime p. It is described in detail by .Its representing spectrum is denoted by BP.-Complex cobordism and Quillen's idempotent:...
, Morava K-theoryMorava K-theoryIn stable homotopy theory, a branch of mathematics, Morava K-theory is one of a collection of cohomology theories introduced in algebraic topology by Jack Morava in unpublished preprints in the early 1970s...
, Morava E-theory, and other theories defined using the algebra of formal groups. - Various flavours of elliptic homologyElliptic cohomologyIn mathematics, elliptic cohomology is a cohomology theory in the sense of algebraic topology. It is related to elliptic curves and modular forms.-History and motivation:Historically, elliptic cohomology arose from the study of elliptic genera...
These are called generalised homology theories; they carry much richer information than ordinary homology, but are often harder to compute. Their study is tightly linked (via the Brown representability theorem) to stable homotopy.
Homological algebra and homology of other objects
A chain complexChain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
consists of groups
 (for all
(for all  ) and homomorphisms
) and homomorphisms  satisfying
satisfying  . This condition shows that the groups
. This condition shows that the groups  are contained in the groups
are contained in the groups  , so one can form the quotient groups
, so one can form the quotient groups  , which are called the homology groups of the original complex. There is a similar theory of cochain complexes, consisting of groups
, which are called the homology groups of the original complex. There is a similar theory of cochain complexes, consisting of groups  and homomorphisms
and homomorphisms  . The simplicial, singular, Čech and Alexander–Spanier groups are all defined by first constructing a chain complex or cochain complex, and then taking its homology. Thus, a substantial part of the work in setting up these groups involves the general theory of chain and cochain complexes, which is known as homological algebra.
. The simplicial, singular, Čech and Alexander–Spanier groups are all defined by first constructing a chain complex or cochain complex, and then taking its homology. Thus, a substantial part of the work in setting up these groups involves the general theory of chain and cochain complexes, which is known as homological algebra.One can also associate (co)chain complexes to a wide variety of other mathematical objects, and then take their (co)homology. For example, there are cohomology modules for groups, Lie algebras and so on.

