
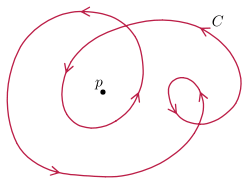
Total curvature
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
study of the differential geometry of curves
Differential geometry of curves
Differential geometry of curves is the branch of geometry that dealswith smooth curves in the plane and in the Euclidean space by methods of differential and integral calculus....
, the total curvature of an immersed plane curve is the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
along a curve taken with respect to arclength:

The total curvature of a closed curve is always an integer multiple of 2π, called the index of the curve, or turning number – it is the winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
of the unit tangent about the origin, or equivalently the degree of the map to the unit circle assigning to each point of the curve, the unit velocity vector at that point. This map is similar to the Gauss map
Gauss map
In differential geometry, the Gauss map maps a surface in Euclidean space R3 to the unit sphere S2. Namely, given a surface X lying in R3, the Gauss map is a continuous map N: X → S2 such that N is a unit vector orthogonal to X at p, namely the normal vector to X at p.The Gauss map can be defined...
for surfaces.
Comparison to surfaces
This relationship between a local invariant, the curvature, and a global topological invariant, the index, is characteristic of results in higher-dimensional Riemannian geometryRiemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
such as the Gauss–Bonnet theorem
Gauss–Bonnet theorem
The Gauss–Bonnet theorem or Gauss–Bonnet formula in differential geometry is an important statement about surfaces which connects their geometry to their topology...
.
Invariance
According to the Whitney–Graustein theorem, the total curvature is invariant under a regular homotopyRegular homotopy
In the mathematical field of topology, a regular homotopy refers to a special kind of homotopy between immersions of one manifold in another. The homotopy must be a 1-parameter family of immersions....
of a curve: it is the degree of the Gauss map
Gauss map
In differential geometry, the Gauss map maps a surface in Euclidean space R3 to the unit sphere S2. Namely, given a surface X lying in R3, the Gauss map is a continuous map N: X → S2 such that N is a unit vector orthogonal to X at p, namely the normal vector to X at p.The Gauss map can be defined...
. However, it is not invariant under homotopy: passing through a kink (cusp) changes the turning number by 1.
By contrast, winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
about a point is invariant under homotopies that do not pass through the point, and changes by 1 if one passes through the point.
Generalizations
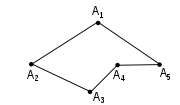
Polygonal chain
A polygonal chain, polygonal curve, polygonal path, or piecewise linear curve, is a connected series of line segments. More formally, a polygonal chain P is a curve specified by a sequence of points \scriptstyle called its vertices so that the curve consists of the line segments connecting the...
s that do not go back on themselves (no 180° angles) have well-defined total curvature, interpreting the curvature as point masses at the angles.
The total curvature of a curve γ in a higher dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
(equipped with its arclength parameterization) can be obtained by flattening out the tangent developable
Tangent developable
The tangent developable of a space curve \gamma is a ruled surface of the form \gamma+s \gamma^\prime. Intuitively it is the union of the tangent lines to the space curve....
to γ into a plane, and computing the total curvature of the resulting curve. That is, the total curvature of a curve in n-dimensional space is
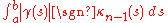
where κn−1 is last Frenet curvature (the torsion
Torsion of curves
In the elementary differential geometry of curves in three dimensions, the torsion of a curve measures how sharply it is twisting. Taken together,the curvature and the torsion of a space curve are analogous to the curvature of a plane curve...
of the curve) and sgn is the signum function.
The minimum total curvature of any three-dimensional curve representing a given knot
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
is an invariant
Knot invariant
In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...
of the knot. This invariant has the value 2π for the unknot, but by the Fary–Milnor theorem it is at least 4π for any other knot.

