
Stick number
Encyclopedia
In the mathematical theory of knots
, the stick number is a knot invariant
that intuitively gives the smallest number of straight "sticks" stuck end to end needed to form a knot. Specifically, given any knot K, the stick number of K, denoted by stick(K), is the smallest number of edges of a polygonal path equivalent to K.
There are few knots whose stick number can be determined exactly. Gyo Taek Jin determined the stick number of a (p, q)-torus knot
T(p, q) in case the parameters p and q are not too far from each other (Jin 1997):
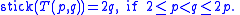
The same result was found independently around the same time by a research group around Colin Adams
, but for a smaller range of parameters (Adams et al. 1997). They also found the following upper bound for the behavior of stick number under knot sum (Adams et al. 1997, Jin 1997):
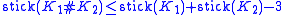
The stick number of a knot K is related to its crossing number
c(K) by the following inequalities (Negami 1991, Calvo 2001):
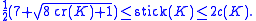
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, the stick number is a knot invariant
Knot invariant
In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...
that intuitively gives the smallest number of straight "sticks" stuck end to end needed to form a knot. Specifically, given any knot K, the stick number of K, denoted by stick(K), is the smallest number of edges of a polygonal path equivalent to K.
There are few knots whose stick number can be determined exactly. Gyo Taek Jin determined the stick number of a (p, q)-torus knot
Torus knot
In knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime integers p and q. A torus link arises if p and q...
T(p, q) in case the parameters p and q are not too far from each other (Jin 1997):
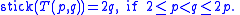
The same result was found independently around the same time by a research group around Colin Adams
Colin Adams (mathematician)
Colin Conrad Adams is a mathematician primarily working in the areas of hyperbolic 3-manifolds and knot theory. His book, The Knot Book, has been praised for its accessible approach to advanced topics in knot theory. He is currently Francis Christopher Oakley Third Century Professor of...
, but for a smaller range of parameters (Adams et al. 1997). They also found the following upper bound for the behavior of stick number under knot sum (Adams et al. 1997, Jin 1997):
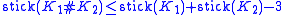
The stick number of a knot K is related to its crossing number
Crossing number (knot theory)
In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....
c(K) by the following inequalities (Negami 1991, Calvo 2001):
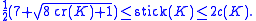
Introductory material
- C. C. Adams. Why knot: knots, molecules and stick numbers. Plus Magazine, May 2001. An accessible introduction into the topic, also for readers with little mathematical background.
- C. C. Adams, The Knot Book: An elementary introduction to the mathematical theory of knots. American Mathematical Society, Providence, RI, 2004. xiv+307 pp. ISBN 0-8218-3678-1
Research articles
- C. C. Adams, B. M. Brennan, D. L. Greilsheimer, A. K. Woo. Stick numbers and composition of knots and links. J. Knot Theory Ramifications 6(2):149–161, 1997.
- J. A. Calvo. Geometric knot spaces and polygonal isotopy. J. Knot Theory Ramifications 10(2):245–267, 2001.
- G. T. Jin. Polygon indices and superbridge indices of torus knots and links. J. Knot Theory Ramifications 6(2):281–289, 1997.
- S. Negami. Ramsey theorems for knots, links and spatial graphs. Trans. Amer. Math. Soc. 324(2):527–541, 1991.

