Finite type invariant
Encyclopedia
In the mathematical theory of knots
, a finite type invariant is a knot invariant that can be extended (in a precise manner to be described) to an invariant of certain singular knots that vanishes on singular knots with m + 1 singularities and does not vanish on some singular knot with 'm' singularities. It is then said to be of type or order m.
We give the combinatorial definition of finite type invariant due to Goussarov, and (independently) Joan Birman
and Xiao-Song Lin. Let V be a knot invariant. Define V1 to be defined on a knot with one transverse singularity.
Consider a knot K to be a smooth embedding of a circle into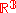
. Let K be a smooth immersion of a circle into 
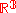with one transverse double point. Then 
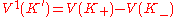, where 
is obtained from K by resolving the double point by pushing up one strand above the other, and K_- is obtained similarly by pushing the opposite strand above the other. We can do this for maps with two transverse double points, three transverse double points, etc., by using the above relation. For V to be of finite type means precisely that there must be a positive integer m such that V vanishes on maps with m + 1 transverse double points.
Furthermore, note that there is notion of equivalence of knots with singularities being transverse double points and V should respect this equivalence. There is also a notion of finite type invariant for 3-manifold
s.
.
Any coefficient of the Kontsevich invariant
is a finite type invariant.
The Milnor invariants are finite type invariants of string links.
have proved that all Vassiliev invariants can be represented by chord diagrams. Using such diagrams, they gave a description of the first nontrivial invariants of orders 2 and 3.
proved the following important theorem about Vassiliev invariants: For every knot one can compute an integral, now called the Kontsevich integral, which is a universal Vassiliev invariant, meaning that every Vassiliev invariant can be obtained from it by an appropriate evaluation. It is not known at present whether the Kontsevich integral, or the totality of Vassiliev invariants, is a complete knot invariant. Computation of the Kontsevich integral, which has values in an algebra
of chord diagrams, turns out to be rather difficult and has been done only for a few classes of knots up to now. There is no finite-type invariant of degree less than 11 which distinguishes mutant knots.
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, a finite type invariant is a knot invariant that can be extended (in a precise manner to be described) to an invariant of certain singular knots that vanishes on singular knots with m + 1 singularities and does not vanish on some singular knot with 'm' singularities. It is then said to be of type or order m.
We give the combinatorial definition of finite type invariant due to Goussarov, and (independently) Joan Birman
Joan Birman
Joan Sylvia Lyttle Birman is an American mathematician, specializing in braid theory and knot theory. Her book Braids, Links, and Mapping Class Groups has become a standard introduction, with many of today's researchers having learned the subject through it...
and Xiao-Song Lin. Let V be a knot invariant. Define V1 to be defined on a knot with one transverse singularity.
Consider a knot K to be a smooth embedding of a circle into
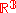. Let K be a smooth immersion of a circle into 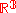with one transverse double point. Then 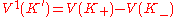, where is obtained from K by resolving the double point by pushing up one strand above the other, and K_- is obtained similarly by pushing the opposite strand above the other. We can do this for maps with two transverse double points, three transverse double points, etc., by using the above relation. For V to be of finite type means precisely that there must be a positive integer m such that V vanishes on maps with m + 1 transverse double points.Furthermore, note that there is notion of equivalence of knots with singularities being transverse double points and V should respect this equivalence. There is also a notion of finite type invariant for 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s.
Examples
The simplest nontrivial Vassiliev invariant of knots is given by the coefficient of the quadratic term of the Alexander–Conway polynomial. It is an invariant of order two. Modulo two, it is equal to the Arf invariantArf invariant (knot)
In the mathematical field of knot theory, the Arf invariant of a knot, named after Cahit Arf, is a knot invariant obtained from a quadratic form associated to a Seifert surface...
.
Any coefficient of the Kontsevich invariant
Kontsevich invariant
In the mathematical theory of knots, the Kontsevich invariant, also known as the Kontsevich integral, of an oriented framed link is the universal finite type invariant in the sense that any coefficient of the Kontsevich invariant is a finite type invariant, and any finite type invariant can be...
is a finite type invariant.
The Milnor invariants are finite type invariants of string links.
Invariants representation
Michael Polyak and Oleg ViroOleg Viro
Oleg Viro is a mathematician in the fields of topology and algebraic geometry, most notably real algebraic geometry, tropical geometry and knot theory....
have proved that all Vassiliev invariants can be represented by chord diagrams. Using such diagrams, they gave a description of the first nontrivial invariants of orders 2 and 3.
The universal Vassiliev invariant
In 1993, Maxim KontsevichMaxim Kontsevich
Maxim Lvovich Kontsevich is a Russian mathematician. He is a professor at the Institut des Hautes Études Scientifiques and a distinguished professor at the University of Miami...
proved the following important theorem about Vassiliev invariants: For every knot one can compute an integral, now called the Kontsevich integral, which is a universal Vassiliev invariant, meaning that every Vassiliev invariant can be obtained from it by an appropriate evaluation. It is not known at present whether the Kontsevich integral, or the totality of Vassiliev invariants, is a complete knot invariant. Computation of the Kontsevich integral, which has values in an algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
of chord diagrams, turns out to be rather difficult and has been done only for a few classes of knots up to now. There is no finite-type invariant of degree less than 11 which distinguishes mutant knots.