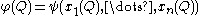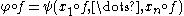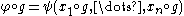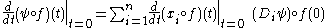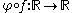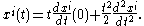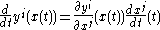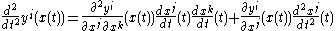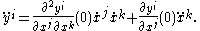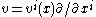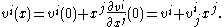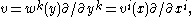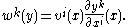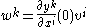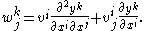Jet (mathematics)
Encyclopedia
In mathematics
, the jet is an operation which takes a differentiable function
f and produces a polynomial
, the truncated Taylor polynomial of f, at each point of its domain. Although this is the definition of a jet, the theory of jets regards these polynomials as being abstract polynomials rather than polynomial functions.
This article first explores the notion of a jet of a real valued function in one real variable, followed by a discussion of generalizations to several real variables. It then gives a rigorous construction of jets and jet spaces between Euclidean space
s. It concludes with a description of jets between manifold
s, and how these jets can be constructed intrinsically. In this more general context, it summarizes some of the applications of jets to differential geometry and the theory of differential equations.
is a real-valued function having at least k+1 derivative
s in a neighborhood U of the point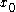
. Then by Taylor's theorem,
where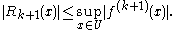
Then the k-jet of f at the point
is defined to be the polynomial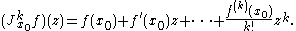
Jets are normally regarded as abstract polynomials in the variable z, not as actual polynomial functions in that variable. In other words, z is an indeterminate variable
allowing one to perform various algebraic operations
among the jets. It is in fact the base-point
from which jets derive their functional dependency. Thus, by varying the base-point, a jet yields a polynomial of order at most "k" at every point. This marks an important conceptual distinction between jets and truncated Taylor series: ordinarily a Taylor series is regarded as depending functionally on its variable, rather than its base-point. Jets, on the other hand, separate the algebraic properties of Taylor series from their functional properties. We shall deal with the reasons and applications of this separation later in the article.
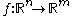is a function from one Euclidean space to another having at least (k+1) derivatives. In this case, Taylor's theorem
asserts that
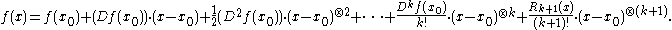
In this case, the k-jet of f is defined to be the polynomial
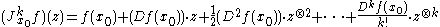
in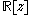
, where 
.
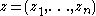If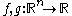
are a pair of real-valued functions, then we can define the product of their jets via
.
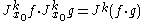Here we have suppressed the indeterminate z, since it is understood that jets are formal polynomials. This product is just the product of ordinary polynomials in z, modulo
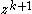. In other words, it is multiplication in the ring 
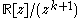, where 
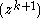is the ideal generated by polynomials homogeneous of order ≥ k+1.
We now move to the composition of jets. To avoid unnecessary technicalities, we consider jets of functions which map the origin to the origin. If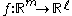
and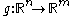 
with f(0)=0 and g(0)=0, then 
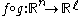. The composition of jets is defined by
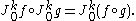
It is readily verified, using the chain rule
, that this constitutes an associative noncommutative operation on the space of jets at the origin.
In fact, the composition of k-jets is nothing more than the composition of polynomials modulo the ideal of polynomials homogeneous of order
.
Examples:
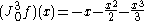
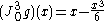
and
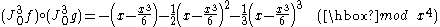
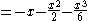
to define jets and jet spaces. It can be generalized to smooth functions between Banach spaces, analytic functions between real or complex domains
, to p-adic analysis
, and to other areas of analysis.
Let
be the vector space
of smooth function
s
. Let k be a non-negative integer, and let p be a point of 
. We define an equivalence relation
on this space by declaring that two functions f and g are equivalent to order k if f and g have the same value at p, and all of their partial derivative
s agree at p up to (and including) their k-th order derivatives. In short,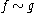
iff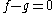 
to k-th order.
The k-th order jet space of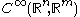
at p is defined to be the set of equivalence classes of 
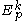, and is denoted by 
.
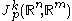The k-th order jet at p of a smooth function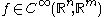
is defined to be the equivalence class of f in 
.
and commutative algebra
to establish the notion of a jet and a jet space. Although this definition is not particularly suited for use in algebraic geometry per se, since it is cast in the smooth category, it can easily be tailored to such uses.
Let
be the vector space
of germs
of smooth function
s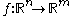
at a point p in 
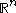. Let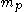 
be the ideal of functions which vanish at p. (This is the maximal ideal
for the local ring
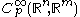.) Then the ideal 
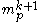consists of all function germs which vanish to order k at p. We may now define the jet space at p by
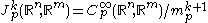
If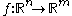
is a smooth function, we may define the k-jet of f at p as the element of 
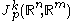by setting
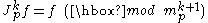
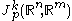and 
. So in the Euclidean context, jets are typically identified with their polynomial representatives under this isomorphism.
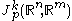of jets at a point 
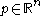. The subspace of this consisting of jets of functions f such that f(p)=q is denoted by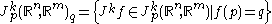
, how do we define the jet of a function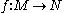
? We could perhaps attempt to define such a jet by using local coordinates
on M and N. The disadvantage of this is that jets cannot thus be defined in an equivariant
fashion. Jets do not transform as tensors. Instead, jets of functions between two manifolds belong to a jet bundle
.
This section begins by introducing the notion of jets of functions from the real line to a manifold. It proves that such jets form a fibre bundle, analogous to the tangent bundle
, which is an associated bundle of a jet group
. It proceeds to address the problem of defining the jet of a function between two smooth manifolds. Throughout this section, we adopt an analytic approach to jets. Although an algebro-geometric approach is also suitable for many more applications, it is too subtle to be dealt with systematically here. See jet (algebraic geometry) for more details.
s through p, by which we henceforth mean smooth functions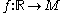
such that f(0)=p. Define an equivalence relation 
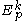as follows. Let f and g be a pair of curves through p. We will then say that f and g are equivalent to order k at p if there is some neighborhood U of p, such that, for every smooth function 
, 
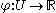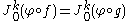. Note that these jets are well-defined since the composite functions 
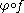and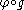 
are just mappings from the real line to itself. This equivalence relation is sometimes called that of k-th order contact
between curves at p.
We now define the k-jet of a curve f through p to be the equivalence class of f under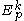
, denoted 
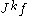or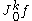 
. The k-th order jet space 
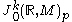is then the set of k-jets at p. This forms a real vector space.
As p varies over M,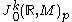
forms a fibre bundle over M: the k-th order tangent bundle
, often denoted in the literature by TkM (although this notation occasionally can lead to confusion). In the case k=1, then the first order tangent bundle is the usual tangent bundle: T1M=TM.
To prove that TkM is in fact a fibre bundle, it is instructive to examine the properties of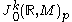
in local coordinates. Let (xi)= (x1,...,xn) be a local coordinate system for M in a neighborhood U of p. Abusing notation
slightly, we may regard (xi) as a local diffeomorphism
.
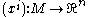Claim. Two curves f and g through p are equivalent modulo
if and only if 
.
Hence the ostensible fibre bundle TkM admits a local trivialization in each coordinate neighborhood. At this point, in order to prove that this ostensible fibre bundle is in fact a fibre bundle, it suffices to establish that it has non-singular transition functions under a change of coordinates. Let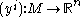
be a different coordinate system and let 
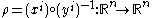be the associated change of coordinates diffeomorphism of Euclidean space to itself. By means of an affine transformation
of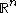
, we may assume without loss of generality
that ρ(0)=0. With this assumption, it suffices to prove that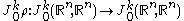
is an invertible transformation under jet composition. (See also jet group
s.) But since ρ is a diffeomorphism,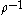
is a smooth mapping as well. Hence,
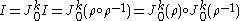
which proves that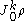
is non-singular. Furthermore, it is smooth, although we do not prove that fact here.
Intuitively, this means that we can express the jet of a curve through p in terms of its Taylor series in local coordinates on M.
Examples in local coordinates:
Suppose that M and N are two smooth manifolds. Let p be a point of M. Consider the space
consisting of smooth maps 
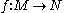defined in some neighborhood of p. We define an equivalence relati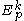on 
on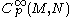 
as follows. Two maps f and g are said to be equivalent if, for every curve γ through p (recall that by our conventions this is a mapping 
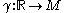such that 
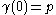), we have 
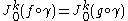on some neighborhood of 0.
The jet space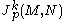
is then defined to be the set of equivalence classes of 
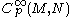modulo the equivalence relation 
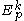. Note that because the target space N need not possess any algebraic structure, 
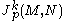also need not have such a structure. This is, in fact, a sharp contrast with the case of Euclidean spaces.
If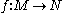
is a smooth function defined near p, then we define the k-jet of f at p, 
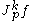, to be the equivalence class of f modulo 
.
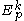. Almost everything in this section generalizes mutatis mutandis
to the case of local sections of a fibre bundle, a Banach bundle
over a Banach manifold
, a fibered manifold
, or quasi-coherent sheaves over schemes
. Furthermore, these examples of possible generalizations are certainly not exhaustive.
Suppose that E is a finite-dimensional smooth vector bundle over a manifold M, with projection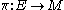
. Then sections of E are smooth functions 
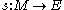such that 
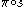is the identity automorphism
of M. The jet of a section s over a neighborhood of a point p is just the jet of this smooth function from M to E at p.
The space of jets of sections at p is denoted by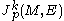
. Although this notation can lead to confusion with the more general jet spaces of functions between two manifolds, the context typically eliminates any such ambiguity.
Unlike jets of functions from a manifold to another manifold, the space of jets of sections at p carries the structure of a vector space inherited from the vector space structure on the sections themselves. As p varies over M, the jet spaces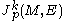
form a vector bundle over M, the k-th order jet bundle
of E, denoted by Jk(E).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the jet is an operation which takes a differentiable function
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
f and produces a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
, the truncated Taylor polynomial of f, at each point of its domain. Although this is the definition of a jet, the theory of jets regards these polynomials as being abstract polynomials rather than polynomial functions.
This article first explores the notion of a jet of a real valued function in one real variable, followed by a discussion of generalizations to several real variables. It then gives a rigorous construction of jets and jet spaces between Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s. It concludes with a description of jets between manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s, and how these jets can be constructed intrinsically. In this more general context, it summarizes some of the applications of jets to differential geometry and the theory of differential equations.
Jets of functions between Euclidean spaces
Before giving a rigorous definition of a jet, it is useful to examine some special cases.Example: One-dimensional case
Suppose that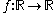 is a real-valued function having at least k+1 derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s in a neighborhood U of the point
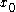. Then by Taylor's theorem,where
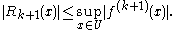
Then the k-jet of f at the point
is defined to be the polynomial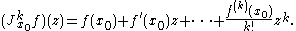Jets are normally regarded as abstract polynomials in the variable z, not as actual polynomial functions in that variable. In other words, z is an indeterminate variable
Indeterminate (variable)
In mathematics, and particularly in formal algebra, an indeterminate is a symbol that does not stand for anything else but itself. In particular it does not designate a constant, or a parameter of the problem, it is not an unknown that could be solved for, it is not a variable designating a...
allowing one to perform various algebraic operations
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
among the jets. It is in fact the base-point
from which jets derive their functional dependency. Thus, by varying the base-point, a jet yields a polynomial of order at most "k" at every point. This marks an important conceptual distinction between jets and truncated Taylor series: ordinarily a Taylor series is regarded as depending functionally on its variable, rather than its base-point. Jets, on the other hand, separate the algebraic properties of Taylor series from their functional properties. We shall deal with the reasons and applications of this separation later in the article.Example: Mappings from one Euclidean space to another
Suppose that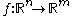 is a function from one Euclidean space to another having at least (k+1) derivatives. In this case, Taylor's theoremTaylor's theorem
In calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the...
asserts that
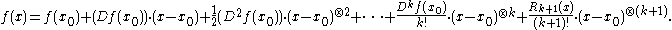
In this case, the k-jet of f is defined to be the polynomial
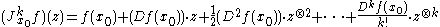
in
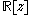, where 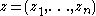.Example: Algebraic properties of jets
There are two basic algebraic structures jets can carry. The first is a product structure, although this ultimately turns out to be the least important. The second is the structure of the composition of jets.If
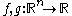are a pair of real-valued functions, then we can define the product of their jets via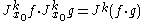.Here we have suppressed the indeterminate z, since it is understood that jets are formal polynomials. This product is just the product of ordinary polynomials in z, modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
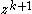. In other words, it is multiplication in the ring 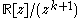, where 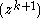is the ideal generated by polynomials homogeneous of order ≥ k+1.We now move to the composition of jets. To avoid unnecessary technicalities, we consider jets of functions which map the origin to the origin. If
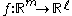and 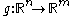with f(0)=0 and g(0)=0, then 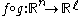. The composition of jets is defined by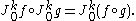It is readily verified, using the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
, that this constitutes an associative noncommutative operation on the space of jets at the origin.
In fact, the composition of k-jets is nothing more than the composition of polynomials modulo the ideal of polynomials homogeneous of order
.Examples:
- In one-dimension, let
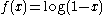and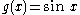 
. Then
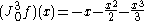
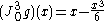
and
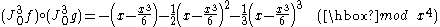
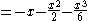
Jets at a point in Euclidean space: Rigorous definitions
This subsection focuses on two different rigorous definitions of the jet of a function at a point, followed by a discussion of Taylor's theorem. These definitions shall prove to be useful later on during the intrinsic definition of the jet of a function between two manifolds.An analytic definition
The following definition uses ideas from mathematical analysisMathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
to define jets and jet spaces. It can be generalized to smooth functions between Banach spaces, analytic functions between real or complex domains
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, to p-adic analysis
P-adic analysis
In mathematics, p-adic analysis is a branch of number theory that deals with the mathematical analysis of functions of p-adic numbers....
, and to other areas of analysis.
Let
be the vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s
. Let k be a non-negative integer, and let p be a point of . We define an equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
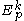on this space by declaring that two functions f and g are equivalent to order k if f and g have the same value at p, and all of their partial derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s agree at p up to (and including) their k-th order derivatives. In short,
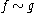iff 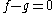to k-th order.The k-th order jet space of
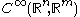at p is defined to be the set of equivalence classes of 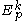, and is denoted by 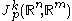.The k-th order jet at p of a smooth function
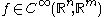is defined to be the equivalence class of f in .An algebro-geometric definition
The following definition uses ideas from algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
and commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
to establish the notion of a jet and a jet space. Although this definition is not particularly suited for use in algebraic geometry per se, since it is cast in the smooth category, it can easily be tailored to such uses.
Let
be the vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of germs
Germ (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
of smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s
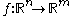at a point p in 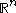. Let 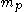be the ideal of functions which vanish at p. (This is the maximal idealMaximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
for the local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
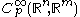.) Then the ideal 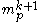consists of all function germs which vanish to order k at p. We may now define the jet space at p by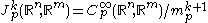If
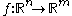is a smooth function, we may define the k-jet of f at p as the element of 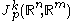by setting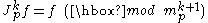Taylor's theorem
Regardless of the definition, Taylor's theorem establishes a canonical isomorphism of vector spaces between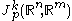 and . So in the Euclidean context, jets are typically identified with their polynomial representatives under this isomorphism.Jet spaces from a point to a point
We have defined the space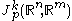 of jets at a point 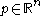. The subspace of this consisting of jets of functions f such that f(p)=q is denoted by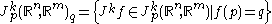Jets of functions between two manifolds
If M and N are two smooth manifoldsDifferentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
, how do we define the jet of a function
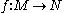? We could perhaps attempt to define such a jet by using local coordinatesManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
on M and N. The disadvantage of this is that jets cannot thus be defined in an equivariant
Equivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
fashion. Jets do not transform as tensors. Instead, jets of functions between two manifolds belong to a jet bundle
Jet bundle
In differential geometry, the jet bundle is a certain construction which makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form...
.
This section begins by introducing the notion of jets of functions from the real line to a manifold. It proves that such jets form a fibre bundle, analogous to the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
, which is an associated bundle of a jet group
Jet group
In mathematics, a jet group is a generalization of the general linear group which applies to Taylor polynomials instead of vectors at a point. Essentially a jet group describes how a Taylor polynomial transforms under changes of coordinate systems .The k-th order jet group Gnk consists of jets of...
. It proceeds to address the problem of defining the jet of a function between two smooth manifolds. Throughout this section, we adopt an analytic approach to jets. Although an algebro-geometric approach is also suitable for many more applications, it is too subtle to be dealt with systematically here. See jet (algebraic geometry) for more details.
Jets of functions from the real line to a manifold
Suppose that M is a smooth manifold containing a point p. We shall define the jets of curveCurve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s through p, by which we henceforth mean smooth functions
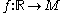such that f(0)=p. Define an equivalence relation 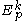as follows. Let f and g be a pair of curves through p. We will then say that f and g are equivalent to order k at p if there is some neighborhood U of p, such that, for every smooth function 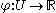, 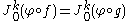. Note that these jets are well-defined since the composite functions 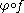and 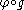are just mappings from the real line to itself. This equivalence relation is sometimes called that of k-th order contactContact (mathematics)
In mathematics, contact of order k of functions is an equivalence relation, corresponding to having the same value at a point P and also the same derivatives there, up to order k. The equivalence classes are generally called jets...
between curves at p.
We now define the k-jet of a curve f through p to be the equivalence class of f under
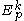, denoted 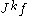or 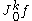. The k-th order jet space 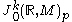is then the set of k-jets at p. This forms a real vector space.As p varies over M,
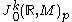forms a fibre bundle over M: the k-th order tangent bundleTangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
, often denoted in the literature by TkM (although this notation occasionally can lead to confusion). In the case k=1, then the first order tangent bundle is the usual tangent bundle: T1M=TM.
To prove that TkM is in fact a fibre bundle, it is instructive to examine the properties of
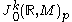in local coordinates. Let (xi)= (x1,...,xn) be a local coordinate system for M in a neighborhood U of p. Abusing notationAbuse of notation
In mathematics, abuse of notation occurs when an author uses a mathematical notation in a way that is not formally correct but that seems likely to simplify the exposition or suggest the correct intuition . Abuse of notation should be contrasted with misuse of notation, which should be avoided...
slightly, we may regard (xi) as a local diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
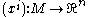.Claim. Two curves f and g through p are equivalent modulo
if and only if .- Indeed, the only if part is clear, since each of the n functions x1,...,xn is a smooth function from M to
. So by the definition of the equivalence relation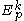 
, two equivalent curves must have 
.
- Conversely, suppose that φ is a smooth real-valued function on M in a neighborhood of p. Since every smooth function has a local coordinate expression, we may express φ as a function in the coordinates. Specifically, if Q is a point of M near p, then
- for some smooth real-valued function ψ of n real variables. Hence, for two curves f and g through p, we have
- The chain rule now establishes the if part of the claim. For instance, if f and g are functions of the real variable t , then
- which is equal to the same expression when evaluated against g instead of f, recalling that f(0)=g(0)=p and f and g are in k-th order contact in the coordinate system (xi).
Hence the ostensible fibre bundle TkM admits a local trivialization in each coordinate neighborhood. At this point, in order to prove that this ostensible fibre bundle is in fact a fibre bundle, it suffices to establish that it has non-singular transition functions under a change of coordinates. Let
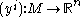be a different coordinate system and let 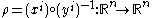be the associated change of coordinates diffeomorphism of Euclidean space to itself. By means of an affine transformationAffine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
of
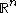, we may assume without loss of generalityWithout loss of generality
Without loss of generality is a frequently used expression in mathematics...
that ρ(0)=0. With this assumption, it suffices to prove that
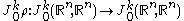is an invertible transformation under jet composition. (See also jet groupJet group
In mathematics, a jet group is a generalization of the general linear group which applies to Taylor polynomials instead of vectors at a point. Essentially a jet group describes how a Taylor polynomial transforms under changes of coordinate systems .The k-th order jet group Gnk consists of jets of...
s.) But since ρ is a diffeomorphism,
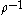is a smooth mapping as well. Hence,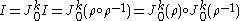which proves that
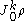is non-singular. Furthermore, it is smooth, although we do not prove that fact here.Intuitively, this means that we can express the jet of a curve through p in terms of its Taylor series in local coordinates on M.
Examples in local coordinates:
- As indicated previously, the 1-jet of a curve through p is a tangent vector. A tangent vector at p is a first-order differential operatorDifferential operatorIn mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
acting on smooth real-valued functions at p. In local coordinates, every tangent vector has the form
- Given such a tangent vector v, let f be the curve given in the xi coordinate system by
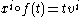. If φ is a smooth function in a neighborhood of p with φ(p)=0, then
- is a smooth real-valued function of one variable whose 1-jet is given by
-
.
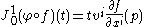- which proves that one can naturally identify tangent vectors at a point with the 1-jets of curves through that point.
- The space of 2-jets of curves through a point.
- In a local coordinate system xi centered at a point p, we can express the second order Taylor polynomial of a curve f(t) by
- So in the x coordinate system, the 2-jet of a curve through p is identified with a list of real numbers
. As with the tangent vectors (1-jets of curves) at a point, 2-jets of curves obey a transformation law upon application of the coordinate transition functions.
- Let (yi) be another coordinate system. By the chain rule,
- Hence, the transformation law is given by evaluating these two expressions at t=0.
- Note that the transformation law for 2-jets is second order in the coordinate transition functions.
Jets of functions from a manifold to a manifold
We are now prepared to define the jet of a function from a manifold to a manifold.Suppose that M and N are two smooth manifolds. Let p be a point of M. Consider the space
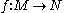consisting of smooth maps defined in some neighborhood of p. We define an equivalence relati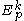on on 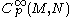as follows. Two maps f and g are said to be equivalent if, for every curve γ through p (recall that by our conventions this is a mapping 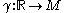such that 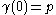), we have 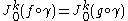on some neighborhood of 0.The jet space
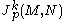is then defined to be the set of equivalence classes of 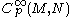modulo the equivalence relation 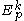. Note that because the target space N need not possess any algebraic structure, 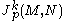also need not have such a structure. This is, in fact, a sharp contrast with the case of Euclidean spaces.If
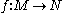is a smooth function defined near p, then we define the k-jet of f at p, 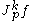, to be the equivalence class of f modulo 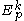.Jets of sections
This subsection deals with the notion of jets of local sections a vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
. Almost everything in this section generalizes mutatis mutandis
Mutatis mutandis
Mutatis mutandis is a Latin phrase meaning "by changing those things which need to be changed" or more simply "the necessary changes having been made"....
to the case of local sections of a fibre bundle, a Banach bundle
Banach bundle
In mathematics, a Banach bundle is a vector bundle each of whose fibres is a Banach space, i.e. a complete normed vector space, possibly of infinite dimension.-Definition of a Banach bundle:...
over a Banach manifold
Banach manifold
In mathematics, a Banach manifold is a manifold modeled on Banach spaces. Thus it is a topological space in which each point has a neighbourhood homeomorphic to an open set in a Banach space...
, a fibered manifold
Fibered manifold
In differential geometry, in the category of differentiable manifolds, a fibered manifold is a surjective submersion \pi \colon E \to B\, , i.e...
, or quasi-coherent sheaves over schemes
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
. Furthermore, these examples of possible generalizations are certainly not exhaustive.
Suppose that E is a finite-dimensional smooth vector bundle over a manifold M, with projection
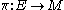. Then sections of E are smooth functions 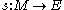such that 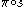is the identity automorphismAutomorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of M. The jet of a section s over a neighborhood of a point p is just the jet of this smooth function from M to E at p.
The space of jets of sections at p is denoted by
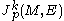. Although this notation can lead to confusion with the more general jet spaces of functions between two manifolds, the context typically eliminates any such ambiguity.Unlike jets of functions from a manifold to another manifold, the space of jets of sections at p carries the structure of a vector space inherited from the vector space structure on the sections themselves. As p varies over M, the jet spaces
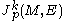form a vector bundle over M, the k-th order jet bundleJet bundle
In differential geometry, the jet bundle is a certain construction which makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form...
of E, denoted by Jk(E).
- Example: The first-order jet bundle of the tangent bundle.
- We work in local coordinates at a point. Consider a vector field
- in a neighborhood of p in M. The 1-jet of v is obtained by taking the first-order Taylor polynomial of the coefficients of the vector field:
- In the x coordinates, the 1-jet at a point can be identified with a list of real numbers
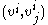. In the same way that a tangent vector at a point can be identified with the list (vi), subject to a certain transformation law under coordinate transitions, we have to know how the list 
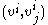is affected by a transition.
- So let us consider the transformation law in passing to another coordinate system yi. Let wk be the coefficients of the vector field v in the y coordinates. Then in the y coordinates, the 1-jet of v is a new list of real numbers
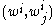. Since
- it follows that
- Expanding by a Taylor series, we have
- Note that the transformation law is second order in the coordinate transition functions.