.gif)
Contact (mathematics)
Encyclopedia
In mathematics
, contact of order k of function
s is an equivalence relation
, corresponding to having the same value at a point P and also the same derivative
s there, up to order k. The equivalence classes are generally called jet
s. The point of osculation is also called the double cusp.
One speaks also of curve
s and geometric objects having k-th order contact at a point: this is also called osculation (i.e. kissing), generalising the property of being tangent
. See for example osculating circle
and osculating orbit
.
Contact forms are particular differential form
s of degree 1 on odd-dimensional manifolds; see contact geometry
. Contact transformations are related changes of co-ordinates, of importance in classical mechanics
. See also Legendre transformation
.
Contact between manifolds is often studied in singularity theory
, where the type of contact are classified, these include the A series (A0: crossing, A1: tangent, A2: osculating, ...) and the umbilic or D-series where there is a high degree of contact with the sphere.
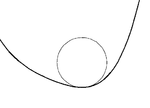
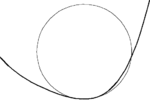
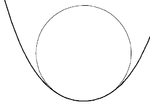For a smooth
curve S in the plane then for each point, S(t) on the curve then there is always exactly one osculating circle which has radius 1/κ(t) where κ(t) is the curvature of the curve at t. If the curve has zero curvature (i.e. an inflection point
on the curve) then the osculating circle will be a straight line. The set of the centers of all the osculating circles form the evolute
of the curve.
If the derivative of curvature κ'(t) is zero, then the osculating circle will have 4-point contact and the curve is said to have a vertex
. The evolute will have a cusp at the center of the circle. The sign of the second derivative of curvature determines whether the curve has a local minimum or maximum of curvature. All closed curves will have at least four vertices, two minima and two maxima (the four-vertex theorem
).
In general a curve will not have 5-point with any circle. However, 5-point contact can occur generically
in a 1-parameter family of curves, where two vertices (one maximum and one minimum) come together and annihilate. At such points the second derivative of curvature will be zero.
. The medial axis
is a sub set of the symmetry set. These sets have been used as a method of characterising the shapes of biological objects.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, contact of order k of function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
, corresponding to having the same value at a point P and also the same derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s there, up to order k. The equivalence classes are generally called jet
Jet (mathematics)
In mathematics, the jet is an operation which takes a differentiable function f and produces a polynomial, the truncated Taylor polynomial of f, at each point of its domain...
s. The point of osculation is also called the double cusp.
One speaks also of curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s and geometric objects having k-th order contact at a point: this is also called osculation (i.e. kissing), generalising the property of being tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
. See for example osculating circle
Osculating circle
In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p...
and osculating orbit
Osculating orbit
In astronomy, and in particular in astrodynamics, the osculating orbit of an object in space is the gravitational Kepler orbit In astronomy, and in particular in astrodynamics, the osculating orbit of an object in space (at a given moment of time) is the gravitational Kepler orbit In astronomy,...
.
Contact forms are particular differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s of degree 1 on odd-dimensional manifolds; see contact geometry
Contact geometry
In mathematics, contact geometry is the study of a geometric structure on smooth manifolds given by a hyperplane distribution in the tangent bundle and specified by a one-form, both of which satisfy a 'maximum non-degeneracy' condition called 'complete non-integrability'...
. Contact transformations are related changes of co-ordinates, of importance in classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
. See also Legendre transformation
Legendre transformation
In mathematics, the Legendre transformation or Legendre transform, named after Adrien-Marie Legendre, is an operation that transforms one real-valued function of a real variable into another...
.
Contact between manifolds is often studied in singularity theory
Singularity theory
-The notion of singularity:In mathematics, singularity theory is the study of the failure of manifold structure. A loop of string can serve as an example of a one-dimensional manifold, if one neglects its width. What is meant by a singularity can be seen by dropping it on the floor...
, where the type of contact are classified, these include the A series (A0: crossing, A1: tangent, A2: osculating, ...) and the umbilic or D-series where there is a high degree of contact with the sphere.
Contact between curves
Two curves in the plane intersecting at a point p are said to have:- 1-point contact if the curves have a simple crossing (not tangent).
- 2-point contact if the two curves are tangentTangentIn geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
. - 3-point contact if the curvatureCurvatureIn mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
s of the curves are equal. Such curves are said to be osculating. - 4-point contact if the derivatives of the curvature are equal.
- 5-point contact if the second derivatives of the curvature are equal.
Contact between a curve and a circle
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
curve S in the plane then for each point, S(t) on the curve then there is always exactly one osculating circle which has radius 1/κ(t) where κ(t) is the curvature of the curve at t. If the curve has zero curvature (i.e. an inflection point
Inflection point
In differential calculus, an inflection point, point of inflection, or inflection is a point on a curve at which the curvature or concavity changes sign. The curve changes from being concave upwards to concave downwards , or vice versa...
on the curve) then the osculating circle will be a straight line. The set of the centers of all the osculating circles form the evolute
Evolute
In the differential geometry of curves, the evolute of a curve is the locus of all its centers of curvature. Equivalently, it is the envelope of the normals to a curve....
of the curve.
If the derivative of curvature κ'(t) is zero, then the osculating circle will have 4-point contact and the curve is said to have a vertex
Vertex (curve)
In the geometry of curves, a vertex is a point of where the first derivative of curvature is zero. This is typically a local maximum or minimum of curvature. Other special cases may occur, for instance when the second derivative is also zero, or when the curvature is constant...
. The evolute will have a cusp at the center of the circle. The sign of the second derivative of curvature determines whether the curve has a local minimum or maximum of curvature. All closed curves will have at least four vertices, two minima and two maxima (the four-vertex theorem
Four-vertex theorem
The four-vertex theorem states that the curvature function of a simple, closed, smooth plane curve has at least four local extrema...
).
In general a curve will not have 5-point with any circle. However, 5-point contact can occur generically
Generic
Generic or Generics may refer to:* Generic mood, a grammatical mood used to make generalized statements like Snow is white* Generic antecedents, referents in linguistic contexts, which are classes...
in a 1-parameter family of curves, where two vertices (one maximum and one minimum) come together and annihilate. At such points the second derivative of curvature will be zero.
Bi-tangents
It is also possible to consider circles which have two point contact with two points S(t1), S(t2) on the curve. Such circles are bi-tangent circles. The centers of all bi-tangent circles form the symmetry setSymmetry set
In geometry, the symmetry set is a method for representing the local symmetries of a curve, and can be used as a method for representing the shape of objects by finding the topological skeleton...
. The medial axis
Medial axis
The medial axis of an object is the set of all points having more than one closest point on the object's boundary. Originally referred to as the topological skeleton, it was introduced by Blum as a tool for biological shape recognition....
is a sub set of the symmetry set. These sets have been used as a method of characterising the shapes of biological objects.