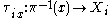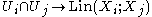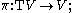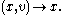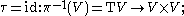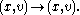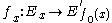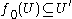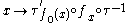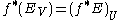Banach bundle
Encyclopedia
In mathematics
, a Banach bundle is a vector bundle
each of whose fibres is a Banach space
, i.e. a complete normed vector space
, possibly of infinite dimension.
of class Cp with p ≥ 0, called the base space; let E be a topological space
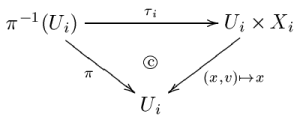
, called the total space; let π : E → M be a surjective continuous map. Suppose that for each point x ∈ M, the fibre Ex = π−1(x) has been given the structure of a Banach space. Let
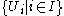
be an open cover of M. Suppose also that for each i ∈ I, there is a Banach space Xi and a map τi
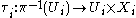
such that
The collection {(Ui, τi)|i∈I} is called a trivialising covering for π : E → M, and the maps τi are called trivialising maps. Two trivialising coverings are said to be equivalent if their union again satisfies the two conditions above. An equivalence class of such trivialising coverings is said to determine the structure of a Banach bundle on π : E → M.
If all the spaces Xi are isomorphic as topological vector spaces, then they can be assumed all to be equal to the same space X. In this case, π : E → M is said to be a Banach bundle with fibre X. If M is a connected space
then this is necessarily the case, since the set of points x ∈ M for which there is a trivialising map
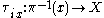
for a given space X is both open
and closed
.
In the finite-dimensional case, the second condition above is implied by the first.
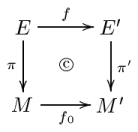
Let π : E → M and π′ : E′ → M′ be two Banach bundles. A Banach bundle morphism from the first bundle to the second consists of a pair of morphisms
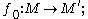
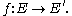
For f to be a morphism means simply that f is a continuous map of topological spaces. If the manifolds M and M′ are both of class Cp, then the requirement that f0 be a morphism is the requirement that it be a p-times continuously differentiable function
. These two morphisms are required to satisfy two conditions (again, the second one is redundant in the finite-dimensional case):
construction to define a new Banach bundle on a second manifold.
Specifically, let π : E → N be a Banach bundle and f : M → N a differentiable map (as usual, everything is Cp). Then the pull-back of π : E → N is the Banach bundle f*π : f*E → M satisfying the following properties:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Banach bundle is a vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
each of whose fibres is a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, i.e. a complete normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
, possibly of infinite dimension.
Definition of a Banach bundle
Let M be a Banach manifoldBanach manifold
In mathematics, a Banach manifold is a manifold modeled on Banach spaces. Thus it is a topological space in which each point has a neighbourhood homeomorphic to an open set in a Banach space...
of class Cp with p ≥ 0, called the base space; let E be a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, called the total space; let π : E → M be a surjective continuous map. Suppose that for each point x ∈ M, the fibre Ex = π−1(x) has been given the structure of a Banach space. Let
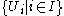
be an open cover of M. Suppose also that for each i ∈ I, there is a Banach space Xi and a map τi
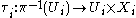
such that
- the map τi is a homeomorphismHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
commuting with the projection onto Ui, i.e. the following diagram commutesCommutative diagramIn mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:
- and for each x ∈ Ui the induced map τix on the fibre Ex
- is an invertible continuous linear map, i.e. an isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
in the categoryCategory (mathematics)In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of topological vector spaceTopological vector spaceIn mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s;
- if Ui and Uj are two members of the open cover, then the map
- is a morphismMorphismIn mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
(a differentiable map of class Cp), where Lin(X; Y) denotes the space of all continuous linear maps from a topological vector space X to another topological vector space Y.
The collection {(Ui, τi)|i∈I} is called a trivialising covering for π : E → M, and the maps τi are called trivialising maps. Two trivialising coverings are said to be equivalent if their union again satisfies the two conditions above. An equivalence class of such trivialising coverings is said to determine the structure of a Banach bundle on π : E → M.
If all the spaces Xi are isomorphic as topological vector spaces, then they can be assumed all to be equal to the same space X. In this case, π : E → M is said to be a Banach bundle with fibre X. If M is a connected space
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
then this is necessarily the case, since the set of points x ∈ M for which there is a trivialising map
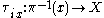
for a given space X is both open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
and closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
.
In the finite-dimensional case, the second condition above is implied by the first.
Examples of Banach bundles
- If V is any Banach space, the tangent spaceTangent spaceIn mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
TxV to V at any point x ∈ V is isomorphic in an obvious way to V itself. The tangent bundleTangent bundleIn differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
TV of V is then a Banach bundle with the usual projection
- This bundle is "trivial" in the sense that TV admits a globally defined trivialising map: the identity functionIdentity functionIn mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
- If M is any Banach manifold, the tangent bundle TM of M forms a Banach bundle with respect to the usual projection, but it may not be trivial.
- Similarly, the cotangent bundleCotangent bundleIn mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
T*M, whose fibre over a point x ∈ M is the topological dual space to the tangent space at x:
- also forms a Banach bundle with respect to the usual projection onto M.
- There is a connection between Bochner spaceBochner spaceIn mathematics, Bochner spaces are a generalization of the concept of Lp spaces to functions whose values lie in a Banach space which is not necessarily the space R or C of real or complex numbers....
s and Banach bundles. Consider, for example, the Bochner space X = L²([0, T]; H1(Ω)), which might arise as a useful object when studying the heat equationHeat equationThe heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
on a domain Ω. One might seek solutions σ ∈ X to the heat equation; for each time t, σ(t) is a function in the Sobolev spaceSobolev spaceIn mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
H1(Ω). One could also think of Y = [0, T] × H1(Ω), which as a Cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
also has the structure of a Banach bundle over the manifold [0, T] with fibre H1(Ω), in which case elements/solutions σ ∈ X are cross sectionSection (fiber bundle)In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
s of the bundle Y of some specified regularity (L², in fact). If the differential geometry of the problem in question is particularly relevant, the Banach bundle point of view might be advantageous.
Morphisms of Banach bundles
The collection of all Banach bundles can be made into a category by defining appropriate morphisms.Let π : E → M and π′ : E′ → M′ be two Banach bundles. A Banach bundle morphism from the first bundle to the second consists of a pair of morphisms
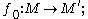
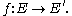
For f to be a morphism means simply that f is a continuous map of topological spaces. If the manifolds M and M′ are both of class Cp, then the requirement that f0 be a morphism is the requirement that it be a p-times continuously differentiable function
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
. These two morphisms are required to satisfy two conditions (again, the second one is redundant in the finite-dimensional case):
- the diagram
- commutes, and, for each x ∈ M, the induced map
- is a continuous linear map;
- for each x0 ∈ M there exist trivialising maps
- such that x0 ∈ U, f0(x0) ∈ U′,
- and the map
- is a morphism (a differentiable map of class Cp).
Pull-back of a Banach bundle
One can take a Banach bundle over one manifold and use the pull-backPullback bundle
In mathematics, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundles. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′...
construction to define a new Banach bundle on a second manifold.
Specifically, let π : E → N be a Banach bundle and f : M → N a differentiable map (as usual, everything is Cp). Then the pull-back of π : E → N is the Banach bundle f*π : f*E → M satisfying the following properties:
- for each x ∈ M, (f*E)x = Ef(x);
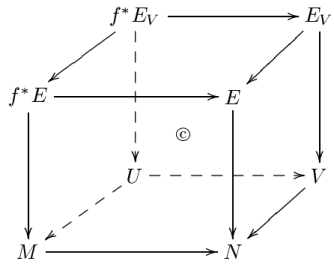
- there is a commutative diagram
- with the top horizontal map being the identity on each fibre;
- if E is trivial, i.e. equal to N × X for some Banach space X, then f*E is also trivial and equal to M × X, and
- is the projection onto the first coordinate;
- if V is an open subset of N and U = f−1(V), then
- and there is a commutative diagram
- where the maps at the "front" and "back" are the same as those in the previous diagram, and the maps from "back" to "front" are (induced by) the inclusions.