
Fibered manifold
Encyclopedia
In differential geometry, in the category of differentiable manifold
s, a fibered manifold is a surjective submersion
 i.e. a surjective differentiable mapping
i.e. a surjective differentiable mapping 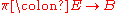 such that at each point
such that at each point 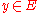 the tangent mapping
the tangent mapping 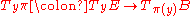 is surjective (equivalently its rank equals dim B).
is surjective (equivalently its rank equals dim B).
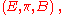 where
where 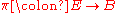 is a surjective submersion, is called a fibered manifold .
is a surjective submersion, is called a fibered manifold .  is called the total space,
is called the total space,  is called the base.
is called the base.
 (resp.
(resp.  ) be an n-dimensional (resp. p-dimensional) manifold. A fibered manifold
) be an n-dimensional (resp. p-dimensional) manifold. A fibered manifold 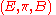 admits fiber charts. We say that a chart
admits fiber charts. We say that a chart
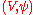 on
on  is a fiber chart, or is adapted to the surjective submersion
is a fiber chart, or is adapted to the surjective submersion  if there exists a chart
if there exists a chart 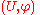 on
on  such that
such that 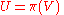 and
and
where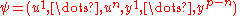 with
with 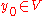 and
and 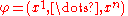 with
with 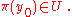 The above fiber chart condition may be equivalently expressed by
The above fiber chart condition may be equivalently expressed by
where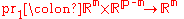 is the first projection. The chart
is the first projection. The chart 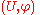 is then obviously unique. In view of the above property, the coordinates of a fiber chart
is then obviously unique. In view of the above property, the coordinates of a fiber chart 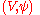 are usually denoted by
are usually denoted by 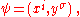 where
where 

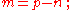 the coordinates of the corresponding chart
the coordinates of the corresponding chart
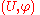 on
on 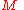 are then denoted, with the obvious convention, by
are then denoted, with the obvious convention, by 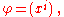 where
where 
Any surjective submersion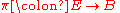 is open: for each open
is open: for each open  the set
the set 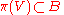 is open in
is open in  .
.
A fibered manifold admits local sections: For each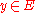 there is an open neighborhood
there is an open neighborhood 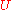 of
of 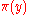 in
in  and a smooth mapping
and a smooth mapping 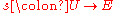 with
with 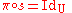 and
and 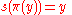 .
.
, the words fiber (Faser in German) and fiber space (gefaserter Raum) appeared for the first time in a paper by Seifert
in 1932 , but his definitions are limited to a very special case. The main difference from the present day conception of a fiber space, however, was that for Seifert what is now called the base space (topological space) of a fiber (topological) space E was not part of the structure, but derived from it as a quotient space of E. The first definition of fiber space is given by Hassler Whitney
in 1935 under the name sphere space, but in 1940 Whitney changed the name to sphere bundle .
The theory of fibered spaces, of which vector bundle
s, principal bundle
s, topological fibration
s and fibered manifold
s are a special case, is attributed to Seifert
, Hopf
, Feldbau , Whitney
, Steenrod, Ehresmann , Serre
, and others.
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
s, a fibered manifold is a surjective submersion
Submersion (mathematics)
In mathematics, a submersion is a differentiable map between differentiable manifolds whose differential is everywhere surjective. This is a basic concept in differential topology...
 i.e. a surjective differentiable mapping
i.e. a surjective differentiable mapping 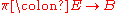 such that at each point
such that at each point 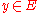 the tangent mapping
the tangent mapping 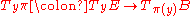 is surjective (equivalently its rank equals dim B).
is surjective (equivalently its rank equals dim B).Formal definition
A triple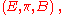 where
where 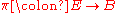 is a surjective submersion, is called a fibered manifold .
is a surjective submersion, is called a fibered manifold .  is called the total space,
is called the total space,  is called the base.
is called the base.Examples
- Every differentiable fiber bundleFiber bundleIn mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
is a fibered manifold. - Every differentiable covering space is a fibered manifold with discrete fiber.
- In general, a fibered manifold needs not to be a fiber bundle: different fibers may have different topologies. An example of this phenomenon may be constructed by taking the trivial bundle
 and deleting two points in to two different fibers over the base manifold
and deleting two points in to two different fibers over the base manifold  .The result is a new fibered manifold where all the fibers except two are connected.
.The result is a new fibered manifold where all the fibers except two are connected.
Properties
Let (resp.
(resp.  ) be an n-dimensional (resp. p-dimensional) manifold. A fibered manifold
) be an n-dimensional (resp. p-dimensional) manifold. A fibered manifold 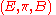 admits fiber charts. We say that a chart
admits fiber charts. We say that a chartChart
A chart is a graphical representation of data, in which "the data is represented by symbols, such as bars in a bar chart, lines in a line chart, or slices in a pie chart"...
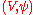 on
on  is a fiber chart, or is adapted to the surjective submersion
is a fiber chart, or is adapted to the surjective submersion  if there exists a chart
if there exists a chart 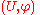 on
on  such that
such that 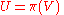 and
and
where
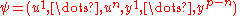 with
with 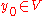 and
and 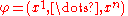 with
with 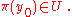 The above fiber chart condition may be equivalently expressed by
The above fiber chart condition may be equivalently expressed by
where
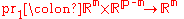 is the first projection. The chart
is the first projection. The chart 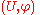 is then obviously unique. In view of the above property, the coordinates of a fiber chart
is then obviously unique. In view of the above property, the coordinates of a fiber chart 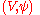 are usually denoted by
are usually denoted by 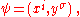 where
where 

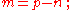 the coordinates of the corresponding chart
the coordinates of the corresponding chartChart
A chart is a graphical representation of data, in which "the data is represented by symbols, such as bars in a bar chart, lines in a line chart, or slices in a pie chart"...
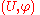 on
on 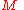 are then denoted, with the obvious convention, by
are then denoted, with the obvious convention, by 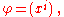 where
where 
Any surjective submersion
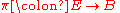 is open: for each open
is open: for each open  the set
the set 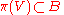 is open in
is open in  .
.A fibered manifold admits local sections: For each
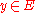 there is an open neighborhood
there is an open neighborhood 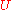 of
of 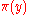 in
in  and a smooth mapping
and a smooth mapping 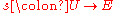 with
with 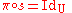 and
and 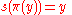 .
.History
In topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, the words fiber (Faser in German) and fiber space (gefaserter Raum) appeared for the first time in a paper by Seifert
Seifert
Seifert is a German surname, and may refer to:*Alfred Seifert, painter*Benjamin Seifert , German cross country skier*Bill Seifert , American racecar driver*Emil Seifert, football manager*Ernst Seifert , German organ builder...
in 1932 , but his definitions are limited to a very special case. The main difference from the present day conception of a fiber space, however, was that for Seifert what is now called the base space (topological space) of a fiber (topological) space E was not part of the structure, but derived from it as a quotient space of E. The first definition of fiber space is given by Hassler Whitney
Hassler Whitney
Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
in 1935 under the name sphere space, but in 1940 Whitney changed the name to sphere bundle .
The theory of fibered spaces, of which vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s, principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
s, topological fibration
Fibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
s and fibered manifold
Fibered manifold
In differential geometry, in the category of differentiable manifolds, a fibered manifold is a surjective submersion \pi \colon E \to B\, , i.e...
s are a special case, is attributed to Seifert
Seifert
Seifert is a German surname, and may refer to:*Alfred Seifert, painter*Benjamin Seifert , German cross country skier*Bill Seifert , American racecar driver*Emil Seifert, football manager*Ernst Seifert , German organ builder...
, Hopf
Hopf
Hopf may refer to:*Eberhard Hopf , Austrian mathematician.*Hans Hopf , German tenor*Heinz Hopf , German mathematician.*Heinz Hopf , Swedish actor.*J. R. Hopf , baseball player....
, Feldbau , Whitney
Whitney
-Places:Canada* Whitney, OntarioUnited Kingdom* Whitney-on-Wye, Herefordshire* Witney, OxfordshireUnited States* Whitney, California, a community in Placer County* Whitney, a neighborhood in Beverly, Visalia, California...
, Steenrod, Ehresmann , Serre
Serre
Serre may refer to:* Claude Serre , a French cartoonist* Jean-Pierre Serre , a French mathematician active in algebraic geometry, number theory and topology* Serre Chevalier, a major French ski resort in the southern part of the Alps...
, and others.



