
Data assimilation
Encyclopedia
Applications of data assimilation arise in many fields of geosciences, perhaps most importantly in weather forecasting
and hydrology
. Data assimilation proceeds by analysis cycles. In each analysis cycle, observations of the current (and possibly, past) state of a system are combined with the results from a numerical weather prediction
model (the forecast) to produce an analysis, which is considered as 'the best' estimate of the current state of the system. This is called the analysis step. Essentially, the analysis step tries to balance the uncertainty in the data and in the forecast. The model is then advanced in time and its result becomes the forecast in the next analysis cycle.
s. The analysis step is an application of the Bayes theorem and the overall assimilation procedure is an example of Recursive Bayesian estimation
. However, the probabilistic analysis is usually simplified to a computationally feasible form. Advancing the probability distribution in time would be done exactly in the general case by the Fokker-Planck equation
, but that is unrealistically expensive, so various approximations operating on simplified representations
of the probability distributions are used instead. If the probability distributions are normal, they can be represented by their mean and covariance, which gives rise to the Kalman filter
. However it is not feasible to maintain the covariance because of the large number of degrees of freedom in the state, so various approximations are used instead.
Many methods represent the probability distributions only by the mean and impute some covariance instead. In the basic form, such analysis step is known as optimal statistical interpolation. Adjusting the initial value of the mathematical model instead of changing the state directly at the analysis time is the essence of the variational methods, 3DVAR and 4DVAR. Nudging
, also known as Newtonian relaxation or 4DDA, is essentially the same as proceeding in continuous time rather than in discrete analysis cycles (the Kalman-Bucy filter), again with imputing simplified covariance.
Ensemble Kalman filter
s represent the probability distribution by an ensemble of simulations, and the covariance is approximated by sample covariance.
In addition to weather forecasting, other uses of DA include trajectory estimation for the Apollo program, GPS, and atmospheric chemistry
.
, and atmospheric pressure
into numerical models as the ones used to predict weather
.
In weather forecasting there are 2 main types of data assimilation: 3 dimensional (3DDA) and 4 dimensional (4DDA). In 3DDA only those observations available at the time of analysis are used. In 4DDA the future observations are included (thus, time dimension added).
s (NWP) forecasts were adjusted by meteorologists using their operational expertise. The objective methods used simple interpolation approaches, and thus were 3DDA methods.
The similar 4DDA methods, called "nudging
" also exist (e.g. in MM5 NWP model). They are based on the simple idea of Newtonian relaxation (the 2nd axiom of Newton). The idea is to add in the right part of dynamical equations of the model a term that is proportional to the difference of the calculated meteorological variable and the observed value. This term that has a negative sign "keeps" the calculated state vector
closer to the observations. Nudging can be interpreted as a variant of the Kalman-Bucy filter (a continuous time version of the Kalman filter
) with the gain matrix prescribed rather than obtained from covariances.
The breakthrough in the field of data assimilation was achieved by L. Gandin (1963) who introduced the "statistical interpolation" (or "optimal interpolation") method. His work developed the previous ideas of Kolmogorov. That method is a 3DDA method and is a type of regression analyses
, which utilizes information about the spatial distributions of covariance
functions of the errors of the "first guess" field (previous forecast) and "true field". These functions are never known. However, the different approximations were assumed.
In fact the optimal interpolation algorithm is the reduced version of the Kalman filtering (KF) algorithm, when the covariance matrices are not calculated from the dynamical equations, but are pre-determined in advance.
Attempts to introduce the KF algorithms as a 4DDA tool for NWP models came later. However, this was (and remains) a very difficult task, since the full version of KF algorithm requires solution of the enormous number of additional equations (~N*N~10**12, where N=Nx*Ny*Nz is the size of the state vector, Nx~100, Ny~100, Nz~100 - the dimensions of the computational grid). To overcome that difficulty the special kind of KF algorithms (approximate or suboptimal KF's) for NWP models were developed. These include, e.g., the Ensemble Kalman filter
and the Reduced-Rank Kalman filters (RRSQRT) (e.g., Todling and Cohn, 1994).
Another significant advance in the development of the 4DDA methods was utilizing the optimal control
theory (variational approach) in the works of Le Dimet and Talagrand (1986), based on the previous works of G. Marchuk, who was the first to apply that theory in the environmental modeling. The significant advantage of the variational approaches is that the meteorological fields satisfy the dynamical equations of the NWP model and at the same time they minimize the functional, characterizing their difference from observations. Thus, the problem of constrained minimization is solved. The 3DDA variational methods were developed for the first time by Sasaki (1958).
As was shown by Lorenc (1986), all the above-mentioned 4DDA methods are in some limit equivalent, i.e. under some assumptions they minimize the same cost function. However, in practical applications these assumptions are never fulfilled, the different methods perform differently and generally it is not clear what approach (Kalman filtering or variational) is better. The fundamental questions also arise in application of the advanced DA techniques such as convergence of the computational method to the global minimum of the functional to be minimised. For instance, cost function or the set in which the solution is sought can be not convex. The 4DDA method which is currently most successful is hybrid incremental 4D-Var, where an ensemble is used to augment the climatological background error covariances at the start of the data assimilation time window, but the background error covariances are evolved during the time window by a simplified version of the NWP
forecast model. This data assimilation method is used operationally at forecast centres such as the Met Office
.
The question is: can the principal limit of the predictability
of weather forecast models be overcome (and to what extent) with the help of data assimilation?
1. 3D-Var

where denotes the background error covariance,
denotes the background error covariance,  the observational error covariance.
the observational error covariance.
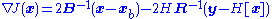
2. 4D-var
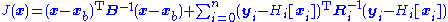
provided that is linear operator (matrix).
is linear operator (matrix).
forecasting. Basically, the same types of data assimilation methods as those described above are in use there. An example of chemical data assimilation using Autochem
can be found at CDACentral.
Given the abundance of spacecraft data for other planets in the Solar System, data assimilation is now also applied beyond the Earth to obtain re-analyses of the atmospheric state of extra-terrestrial planets. Mars is the first extra-terrestrial planet which data assimilation has been applied to, so far. Available spacecraft data include, in particular, retrievals of temperature and dust/water ice optical ticknesses from the Thermal Emission Spectrometer onboard NASA's Mars Global Surveyor
and the Mars Climate Sounder onboard NASA's Mars Reconnaissance Orbiter
. Two methods of data assimilation have been applied to these datasets: an Analysis Correction scheme and two Ensemble Kalman Filter schemes, both using a global circulation model of the martian atmosphere as forward model. The Mars Analysis Correction Data Assimilation (MACDA) dataset is publicly available from the British Atmospheric Data Centre.
Data assimilation is a part of the challenge for every forecasting problem.
Dealing with biased data is a serious challenge in data assimilation. Further development of methods to deal with biases will be of particular use. If there are several instruments observing the same variable then intercomparing them using probability distribution function
s can be instructive. Such an analysis is available on line at PDFCentral designed for the validation of observations from the NASA Aura satellite
.
Other examples of assimilation:
Weather forecasting
Weather forecasting is the application of science and technology to predict the state of the atmosphere for a given location. Human beings have attempted to predict the weather informally for millennia, and formally since the nineteenth century...
and hydrology
Hydrology
Hydrology is the study of the movement, distribution, and quality of water on Earth and other planets, including the hydrologic cycle, water resources and environmental watershed sustainability...
. Data assimilation proceeds by analysis cycles. In each analysis cycle, observations of the current (and possibly, past) state of a system are combined with the results from a numerical weather prediction
Numerical weather prediction
Numerical weather prediction uses mathematical models of the atmosphere and oceans to predict the weather based on current weather conditions. Though first attempted in the 1920s, it was not until the advent of computer simulation in the 1950s that numerical weather predictions produced realistic...
model (the forecast) to produce an analysis, which is considered as 'the best' estimate of the current state of the system. This is called the analysis step. Essentially, the analysis step tries to balance the uncertainty in the data and in the forecast. The model is then advanced in time and its result becomes the forecast in the next analysis cycle.
Data assimilation as statistical estimation
In data assimilation applications, the analysis and forecasts are best thought of as probability distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s. The analysis step is an application of the Bayes theorem and the overall assimilation procedure is an example of Recursive Bayesian estimation
Recursive Bayesian estimation
Recursive Bayesian estimation, also known as a Bayes filter, is a general probabilistic approach for estimating an unknown probability density function recursively over time using incoming measurements and a mathematical process model.-In robotics:...
. However, the probabilistic analysis is usually simplified to a computationally feasible form. Advancing the probability distribution in time would be done exactly in the general case by the Fokker-Planck equation
Fokker-Planck equation
The Fokker–Planck equation describes the time evolution of the probability density function of the velocity of a particle, and can be generalized to other observables as well.It is named after Adriaan Fokkerand Max Planck...
, but that is unrealistically expensive, so various approximations operating on simplified representations
Representation (mathematics)
In mathematics, representation is a very general relationship that expresses similarities between objects. Roughly speaking, a collection Y of mathematical objects may be said to represent another collection X of objects, provided that the properties and relationships existing among the...
of the probability distributions are used instead. If the probability distributions are normal, they can be represented by their mean and covariance, which gives rise to the Kalman filter
Kalman filter
In statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
. However it is not feasible to maintain the covariance because of the large number of degrees of freedom in the state, so various approximations are used instead.
Many methods represent the probability distributions only by the mean and impute some covariance instead. In the basic form, such analysis step is known as optimal statistical interpolation. Adjusting the initial value of the mathematical model instead of changing the state directly at the analysis time is the essence of the variational methods, 3DVAR and 4DVAR. Nudging
Nudging
Nudge, also known as buzz, is a feature of instant messaging software used to get the attention of another user, for example, by shaking the conversation window or playing a sound...
, also known as Newtonian relaxation or 4DDA, is essentially the same as proceeding in continuous time rather than in discrete analysis cycles (the Kalman-Bucy filter), again with imputing simplified covariance.
Ensemble Kalman filter
Ensemble Kalman filter
The ensemble Kalman filter is a recursive filter suitable for problems with a large number of variables, such as discretizations of partial differential equations in geophysical models...
s represent the probability distribution by an ensemble of simulations, and the covariance is approximated by sample covariance.
In addition to weather forecasting, other uses of DA include trajectory estimation for the Apollo program, GPS, and atmospheric chemistry
Autochem
AutoChem is NASA release software that constitutes an automatic computer code generator and documenter for chemically reactive systems written by David Lary between 1993 and the present. It was designed primarily for modeling atmospheric chemistry, and in particular, for chemical data...
.
Weather forecasting applications
Data assimilation is a concept encompassing any method for combining observations of variables like temperatureTemperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
, and atmospheric pressure
Atmospheric pressure
Atmospheric pressure is the force per unit area exerted into a surface by the weight of air above that surface in the atmosphere of Earth . In most circumstances atmospheric pressure is closely approximated by the hydrostatic pressure caused by the weight of air above the measurement point...
into numerical models as the ones used to predict weather
Weather
Weather is the state of the atmosphere, to the degree that it is hot or cold, wet or dry, calm or stormy, clear or cloudy. Most weather phenomena occur in the troposphere, just below the stratosphere. Weather refers, generally, to day-to-day temperature and precipitation activity, whereas climate...
.
In weather forecasting there are 2 main types of data assimilation: 3 dimensional (3DDA) and 4 dimensional (4DDA). In 3DDA only those observations available at the time of analysis are used. In 4DDA the future observations are included (thus, time dimension added).
History of Data Assimilation in Weather forecasting
The first data assimilation methods were called the "objective analyses" (e.g., Cressman algorithm). This was in contrast to the "subjective analyses", when (in past practices) numerical weather predictionNumerical weather prediction
Numerical weather prediction uses mathematical models of the atmosphere and oceans to predict the weather based on current weather conditions. Though first attempted in the 1920s, it was not until the advent of computer simulation in the 1950s that numerical weather predictions produced realistic...
s (NWP) forecasts were adjusted by meteorologists using their operational expertise. The objective methods used simple interpolation approaches, and thus were 3DDA methods.
The similar 4DDA methods, called "nudging
Nudging
Nudge, also known as buzz, is a feature of instant messaging software used to get the attention of another user, for example, by shaking the conversation window or playing a sound...
" also exist (e.g. in MM5 NWP model). They are based on the simple idea of Newtonian relaxation (the 2nd axiom of Newton). The idea is to add in the right part of dynamical equations of the model a term that is proportional to the difference of the calculated meteorological variable and the observed value. This term that has a negative sign "keeps" the calculated state vector
State space (controls)
In control engineering, a state space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations...
closer to the observations. Nudging can be interpreted as a variant of the Kalman-Bucy filter (a continuous time version of the Kalman filter
Kalman filter
In statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
) with the gain matrix prescribed rather than obtained from covariances.
The breakthrough in the field of data assimilation was achieved by L. Gandin (1963) who introduced the "statistical interpolation" (or "optimal interpolation") method. His work developed the previous ideas of Kolmogorov. That method is a 3DDA method and is a type of regression analyses
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
, which utilizes information about the spatial distributions of covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
functions of the errors of the "first guess" field (previous forecast) and "true field". These functions are never known. However, the different approximations were assumed.
In fact the optimal interpolation algorithm is the reduced version of the Kalman filtering (KF) algorithm, when the covariance matrices are not calculated from the dynamical equations, but are pre-determined in advance.
Attempts to introduce the KF algorithms as a 4DDA tool for NWP models came later. However, this was (and remains) a very difficult task, since the full version of KF algorithm requires solution of the enormous number of additional equations (~N*N~10**12, where N=Nx*Ny*Nz is the size of the state vector, Nx~100, Ny~100, Nz~100 - the dimensions of the computational grid). To overcome that difficulty the special kind of KF algorithms (approximate or suboptimal KF's) for NWP models were developed. These include, e.g., the Ensemble Kalman filter
Ensemble Kalman filter
The ensemble Kalman filter is a recursive filter suitable for problems with a large number of variables, such as discretizations of partial differential equations in geophysical models...
and the Reduced-Rank Kalman filters (RRSQRT) (e.g., Todling and Cohn, 1994).
Another significant advance in the development of the 4DDA methods was utilizing the optimal control
Optimal control
Optimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
theory (variational approach) in the works of Le Dimet and Talagrand (1986), based on the previous works of G. Marchuk, who was the first to apply that theory in the environmental modeling. The significant advantage of the variational approaches is that the meteorological fields satisfy the dynamical equations of the NWP model and at the same time they minimize the functional, characterizing their difference from observations. Thus, the problem of constrained minimization is solved. The 3DDA variational methods were developed for the first time by Sasaki (1958).
As was shown by Lorenc (1986), all the above-mentioned 4DDA methods are in some limit equivalent, i.e. under some assumptions they minimize the same cost function. However, in practical applications these assumptions are never fulfilled, the different methods perform differently and generally it is not clear what approach (Kalman filtering or variational) is better. The fundamental questions also arise in application of the advanced DA techniques such as convergence of the computational method to the global minimum of the functional to be minimised. For instance, cost function or the set in which the solution is sought can be not convex. The 4DDA method which is currently most successful is hybrid incremental 4D-Var, where an ensemble is used to augment the climatological background error covariances at the start of the data assimilation time window, but the background error covariances are evolved during the time window by a simplified version of the NWP
Numerical weather prediction
Numerical weather prediction uses mathematical models of the atmosphere and oceans to predict the weather based on current weather conditions. Though first attempted in the 1920s, it was not until the advent of computer simulation in the 1950s that numerical weather predictions produced realistic...
forecast model. This data assimilation method is used operationally at forecast centres such as the Met Office
Met Office
The Met Office , is the United Kingdom's national weather service, and a trading fund of the Department for Business, Innovation and Skills...
.
Future Development in NWP
The rapid development of the various data assimilation methods for NWP models is connected with the two main points in the field of numerical weather prediction:- Utilizing the observations currently seems to be the most promising chance to improve the quality of the forecasts at the different spatial scales (from the planetary scale to the local city, or even street scale) and time scales.
- The number of different kinds of available observations (sodarSODARSODAR , also written as sodar, is a meteorological instrument used as a wind profiler to measure the scattering of sound waves by atmospheric turbulence...
s, radarRadarRadar is an object-detection system which uses radio waves to determine the range, altitude, direction, or speed of objects. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations, and terrain. The radar dish or antenna transmits pulses of radio...
s, satelliteSatelliteIn the context of spaceflight, a satellite is an object which has been placed into orbit by human endeavour. Such objects are sometimes called artificial satellites to distinguish them from natural satellites such as the Moon....
) is rapidly growing.
The question is: can the principal limit of the predictability
Predictability
Predictability is the degree to which a correct prediction or forecast of a system's state can be made either qualitatively or quantitatively.-Predictability and Causality:...
of weather forecast models be overcome (and to what extent) with the help of data assimilation?
Cost function
The process of creating the analysis in data assimilation often involves minimization of a "cost function." A typical cost function would be the sum of the squared deviations of the analysis values from the observations weighted by the accuracy of the observations, plus the sum of the squared deviations of the forecast fields and the analyzed fields weighted by the accuracy of the forecast. This has the effect of making sure that the analysis does not drift too far away from observations and forecasts that are known to usually be reliable.1. 3D-Var

where
 denotes the background error covariance,
denotes the background error covariance,  the observational error covariance.
the observational error covariance.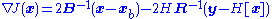
2. 4D-var
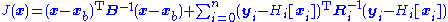
provided that
 is linear operator (matrix).
is linear operator (matrix).Other applications of Data Assimilation
Data assimilation methods are currently also used in other environmental forecasting problems, e.g. in hydrologicalHydrology
Hydrology is the study of the movement, distribution, and quality of water on Earth and other planets, including the hydrologic cycle, water resources and environmental watershed sustainability...
forecasting. Basically, the same types of data assimilation methods as those described above are in use there. An example of chemical data assimilation using Autochem
Autochem
AutoChem is NASA release software that constitutes an automatic computer code generator and documenter for chemically reactive systems written by David Lary between 1993 and the present. It was designed primarily for modeling atmospheric chemistry, and in particular, for chemical data...
can be found at CDACentral.
Given the abundance of spacecraft data for other planets in the Solar System, data assimilation is now also applied beyond the Earth to obtain re-analyses of the atmospheric state of extra-terrestrial planets. Mars is the first extra-terrestrial planet which data assimilation has been applied to, so far. Available spacecraft data include, in particular, retrievals of temperature and dust/water ice optical ticknesses from the Thermal Emission Spectrometer onboard NASA's Mars Global Surveyor
Mars Global Surveyor
The Mars Global Surveyor was a US spacecraft developed by NASA's Jet Propulsion Laboratory and launched November 1996. It began the United States's return to Mars after a 10-year absence. It completed its primary mission in January 2001 and was in its third extended mission phase when, on 2...
and the Mars Climate Sounder onboard NASA's Mars Reconnaissance Orbiter
Mars Reconnaissance Orbiter
Mars Reconnaissance Orbiter is a NASA multipurpose spacecraft designed to conduct reconnaissance and Exploration of Mars from orbit...
. Two methods of data assimilation have been applied to these datasets: an Analysis Correction scheme and two Ensemble Kalman Filter schemes, both using a global circulation model of the martian atmosphere as forward model. The Mars Analysis Correction Data Assimilation (MACDA) dataset is publicly available from the British Atmospheric Data Centre.
Data assimilation is a part of the challenge for every forecasting problem.
Dealing with biased data is a serious challenge in data assimilation. Further development of methods to deal with biases will be of particular use. If there are several instruments observing the same variable then intercomparing them using probability distribution function
Probability distribution function
Depending upon which text is consulted, a probability distribution function is any of:* a probability distribution function,* a cumulative distribution function,* a probability mass function, or* a probability density function....
s can be instructive. Such an analysis is available on line at PDFCentral designed for the validation of observations from the NASA Aura satellite
Aura (satellite)
Aura is a multi-national NASA scientific research satellite in orbit around the Earth, studying the Earth's ozone layer, air quality and climate. It is the third major component of the Earth Observing System following on Terra and Aqua...
.
External links
Examples of how variational assimilation is implemented weather forecasting at:- ECMWF http://www.ecmwf.int/research/ifsdocs/ASSIMILATION/Chap1_Overview2.html
- the Met OfficeMet OfficeThe Met Office , is the United Kingdom's national weather service, and a trading fund of the Department for Business, Innovation and Skills...
http://www.metoffice.gov.uk/science/creating/first_steps/data_assim.html?zoneid=79046
Other examples of assimilation:

