Radon transform - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the Radon transform in two dimensions, named after the Austrian mathematician Johann Radon

Johann Radon

Johann Karl August Radon was an Austrian mathematician. His doctoral dissertation was on calculus of variations .- Life :...

, is the integral transform consisting of the integral of a function over straight lines. The transform was introduced by Johann Radon

Johann Radon

Johann Karl August Radon was an Austrian mathematician. His doctoral dissertation was on calculus of variations .- Life :...

(1917), who also provided a formula for the inverse transform. Radon further included formulas for the transform in three-dimensions, in which the integral is taken over planes. It was later generalised to higher-dimensional Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

s, and more broadly in the context of integral geometry

Integral geometry

In mathematics, integral geometry is the theory of measures on a geometrical space invariant under the symmetry group of that space. In more recent times, the meaning has been broadened to include a view of invariant transformations from the space of functions on one geometrical space to the...

. The complex

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

analog of the Radon transform is known as the Penrose transform

Penrose transform

In mathematical physics, the Penrose transform, introduced by , is a complex analogue of the Radon transform that relates massless fields on spacetime to cohomology of sheaves on complex projective space...

.
The Radon transform is widely applicable to tomography

Tomography

Tomography refers to imaging by sections or sectioning, through the use of any kind of penetrating wave. A device used in tomography is called a tomograph, while the image produced is a tomogram. The method is used in radiology, archaeology, biology, geophysics, oceanography, materials science,...

, the creation of an image from the scattering

Scattering

Scattering is a general physical process where some forms of radiation, such as light, sound, or moving particles, are forced to deviate from a straight trajectory by one or more localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of...

data associated to cross-sectional scans of an object. If a function ƒ represents an unknown density, then the Radon transform represents the scattering data obtained as the output of a tomographic scan. Hence the inverse of the Radon transform can be used to reconstruct the original density from the scattering data, and thus it forms the mathematical underpinning for tomographic reconstruction

Tomographic reconstruction

The mathematical basis for tomographic imaging was laid down by Johann Radon. It is applied in computed tomography to obtain cross-sectional images of patients...

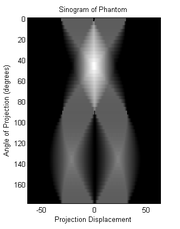
, also known as image reconstruction. The Radon transform data is often called a sinogram because the Radon transform of a Dirac delta function

Dirac delta function

The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...

is a distribution

Generalized function

In mathematics, generalized functions are objects generalizing the notion of functions. There is more than one recognized theory. Generalized functions are especially useful in making discontinuous functions more like smooth functions, and describing physical phenomena such as point charges...

supported on the graph of a sine wave. Consequently the Radon transform of a number of small objects appears graphically as a number of blurred sine waves with different amplitudes and phases. The Radon transform is useful in computed axial tomography (CAT scan), barcode

Barcode

A barcode is an optical machine-readable representation of data, which shows data about the object to which it attaches. Originally barcodes represented data by varying the widths and spacings of parallel lines, and may be referred to as linear or 1 dimensional . Later they evolved into rectangles,...

scanners, electron microscopy of macromolecular assemblies like viruses and protein complexes, reflection seismology

Reflection seismology

Reflection seismology is a method of exploration geophysics that uses the principles of seismology to estimate the properties of the Earth's subsurface from reflected seismic waves. The method requires a controlled seismic source of energy, such as dynamite/Tovex, a specialized air gun or a...

and in the solution of hyperbolic partial differential equations.

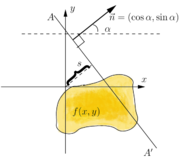
Definition

Let ƒ(x) = ƒ(x,y) be a continuous function

Continuous function

In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...

vanishing outside some large disc in the Euclidean plane R². The Radon transform, Rƒ, is a function defined on the space of straight lines L in R² by the line integral along each such line:

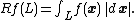
Concretely, any straight line L can be parametrized by

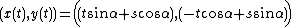
where s is the distance of L from the origin and

is the angle the normal vector to L makes with the x axis. It follows that the quantities (α,s) can be considered as coordinates on the space of all lines in R², and the Radon transform can be expressed in these coordinates by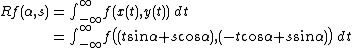

More generally, in the n-dimensional Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

Rⁿ, the Radon transform of a compactly supported continuous function ƒ is a function Rƒ on the space Σ_n of all hyperplane

Hyperplane

A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...

s in Rⁿ. It is defined by

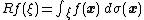
for ξ ∈Σ_n, where the integral is taken with respect to the natural hypersurface measure

Measure (mathematics)

In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...

, dσ (generalizing the |dx| term from the 2-dimensional case). Observe that any element of Σ_n is characterized as the solution locus of an equation

where α ∈ Sⁿ⁻¹ is a unit vector and s ∈ R. Thus the n-dimensional Radon transform may be rewritten as a function on Sⁿ⁻¹×R via

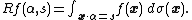
It is also possible to generalize the Radon transform still further by integrating instead over k-dimensional affine subspaces of Rⁿ. The X-ray transform

X-ray transform

In mathematics, the X-ray transform is an integral transform introduced by that is one of the cornerstones of modern integral geometry. It is very closely related to the Radon transform, and coincides with it in two dimensions...

is the most widely used special case of this construction, and is obtained by integrating over straight lines.

Relationship with the Fourier transform

The Radon transform is closely related to the Fourier transform

Fourier transform

In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...

. For a function of one variable the Fourier transform is defined by

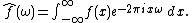
and for a function of a 2-vector

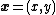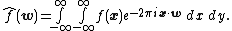
For convenience define

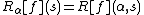as it is only meaningful to take the Fourier transform in the

variable. The Fourier slice theorem then states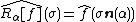

where

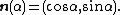
Thus the two-dimensional Fourier transform of the initial function is the one variable Fourier transform of the Radon transform of that function. More generally, one has the result valid in n dimensions

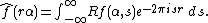
Indeed, the result follows at once by computing the two variable Fourier integral along appropriate slices:

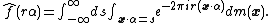
An application of the Fourier inversion formula also gives an explicit inversion formula for the Radon transform, and thus shows that it is invertible on suitably chosen spaces of functions. However this form is not particularly useful for numerical inversion, and faster discrete inversion methods exist.

Dual transform

The dual Radon transform is a kind of adjoint

Adjoint

In mathematics, the term adjoint applies in several situations. Several of these share a similar formalism: if A is adjoint to B, then there is typically some formula of the type = .Specifically, adjoint may mean:...

to the Radon transform. Beginning with a function g on the space Σ_n, the dual Radon transform is the function R^∗g on Rⁿ defined by

The integral here is taken over the set of all lines incident with the point x ∈ Rⁿ, and the measure dμ is the unique probability measure

Probability measure

In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...

on the set

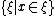invariant under rotations about the point x.

Concretely, for the two-dimensional Radon transform, the dual transform is given by

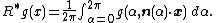
In the context of image processing, the dual transform is commonly called backprojection as it takes a function defined on each line in the plane and 'smears' or projects it back over the line to produce an image. Computationally efficient inversion formulas reconstruct the image from the points where the back-projection lines meet.

Intertwining property

Let Δ denote the Laplacian on Rⁿ: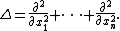

This is a natural rotationally invariant second-order differential operator

Differential operator

In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...

. On Σ_n, the "radial" second derivative

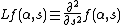
is also rotationally invariant. The Radon transform and its dual are intertwining operators for these two differential operators in the sense that

Inversion formulas

Explicit and computationally efficient inversion formulas for the Radon transform and its dual are available. The Radon transform in n dimensions can be inverted by the formula

where

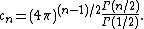
and the power of the Laplacian (−Δ)^(n−1)/2 is defined as a pseudodifferential operator if necessary by the Fourier transform

Fourier transform

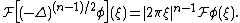
For computational purposes, the power of the Laplacian is commuted with the dual transform R^* to give

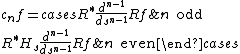
where H_s is the Hilbert transform

Hilbert transform

In mathematics and in signal processing, the Hilbert transform is a linear operator which takes a function, u, and produces a function, H, with the same domain. The Hilbert transform is named after David Hilbert, who first introduced the operator in order to solve a special case of the...

with respect to the s variable. In two dimensions, the operator H_sd/ds appears in image processing as a ramp filter. One can prove directly from the Fourier slice theorem and change of variables for integration that for a compactly supported continuous function ƒ of two variables

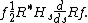
Thus in an image processing context the original image ƒ can be recovered from the 'sinogram' data Rƒ by applying a ramp filter (in the

variable) and then back-projecting. As the filtering step can be performed efficiently (for example using digital signal processing

Digital signal processing

Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...

techniques) and the back projection step is simply an accumulation of values in the pixels of the image, this results in a highly efficient, and hence widely used, algorithm.

Explicitly, the inversion formula obtained by the latter method is

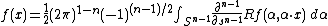
if n is odd, and

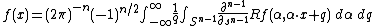
if n is even.

The dual transform can also be inverted by an analogous formula:

Definition

Relationship with the Fourier transform

Dual transform

Intertwining property

Inversion formulas

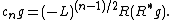
See also