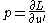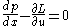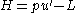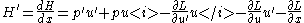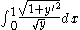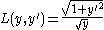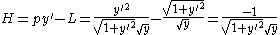Beltrami identity
Encyclopedia
The Beltrami identity is an identity in the calculus of variations
. It says that a function u which is an extremal of the integral
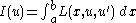
satisfies the differential equation

In the case that L is the Lagrangian of a Mechanical system, and if L does not depend on x explicitly, which corresponds to a Lagrangian which does not explicitly depend on time, the Beltrami identity states that the Hamiltonian associated to the Lagrangian is a conserved energy.
The Euler-Lagrange equation
says
or
define the Hamiltonian H to be the Legendre transform
of L with respect to u:
Then
The second and third term cancel, by the definition of p, and the first and fourth terms cancel by the Euler Lagrange equation. This leaves the Beltrami identity:
which is a special case of Noether's theorem
.
This can be used to solve the Euler-Lagrange equation
, in the same way that conservation of energy can be used to solve Newton's law of motion. The condition that H is constant is an equation for the first derivative of u, while the original Euler Lagrange equation is an equation for the second derivative of u.
For example, consider the Brachistochrone problem: find the curve minimizing the integral:
The quantity to minimize is the integral of an L which does not depend explicitly on time,
so the associated Hamiltonian is constant:
which simplifies to the differential equation for the cycloid.
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
. It says that a function u which is an extremal of the integral
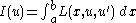
satisfies the differential equation

In the case that L is the Lagrangian of a Mechanical system, and if L does not depend on x explicitly, which corresponds to a Lagrangian which does not explicitly depend on time, the Beltrami identity states that the Hamiltonian associated to the Lagrangian is a conserved energy.
Proof
Define the conjugate momentum p to be the partial derivative of the function L with respect to u'.The Euler-Lagrange equation
Euler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
says
or
define the Hamiltonian H to be the Legendre transform
Legendre transformation
In mathematics, the Legendre transformation or Legendre transform, named after Adrien-Marie Legendre, is an operation that transforms one real-valued function of a real variable into another...
of L with respect to u:
Then
The second and third term cancel, by the definition of p, and the first and fourth terms cancel by the Euler Lagrange equation. This leaves the Beltrami identity:
which is a special case of Noether's theorem
Noether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
.
Application
In case that L is independent of x, then the Beltrami identity states that H is constantThis can be used to solve the Euler-Lagrange equation
Euler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
, in the same way that conservation of energy can be used to solve Newton's law of motion. The condition that H is constant is an equation for the first derivative of u, while the original Euler Lagrange equation is an equation for the second derivative of u.
For example, consider the Brachistochrone problem: find the curve minimizing the integral:
The quantity to minimize is the integral of an L which does not depend explicitly on time,
so the associated Hamiltonian is constant:
which simplifies to the differential equation for the cycloid.