
Singular solution
Encyclopedia
A singular solution ys of an ordinary
differential equation
is a solution that is singular
or one for which the initial value problem
(also called the Cauchy problem by some authors) fails to have a unique solution at some point on the solution. The set on which a solution is singular may be as small as a single point or as large as the full real line. Solutions which are singular in the sense that the initial value problem fails to have a unique solution need not be singular functions
.
In some cases, the term singular solution is used to mean a solution at which there is a failure of uniqueness to the initial value problem at every point on the curve. A singular solution in this stronger sense is often given as tangent
to every solution from a family of solutions. By tangent we mean that there is a point x where ys(x) = yc(x) and y's(x) = y'c(x) where yc is a solution in a family of solutions parameterized by c. This means that the singular solution is the envelope
of the family of solutions.
Usually, singular solutions appear in differential equations when there is a need to divide in a term that might be equal to zero
. Therefore, when one is solving a differential equation and using division one must check what happens if the term is equal to zero, and whether it leads to a singular solution. The Picard–Lindelöf theorem
, which gives sufficient conditions for unique solutions to exist, can be used to rule out the existence of singular solutions. Other theorems, such as the Peano existence theorem
, give sufficient conditions for solutions to exist with out necessarily being unique, which can allow for the existence of singular solutions.

where primes denote derivatives with respect to x. The general solution to this equation is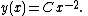
For a given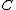 , this solution is smooth except at
, this solution is smooth except at 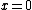 where the solution is divergent. Furthermore, for a given
where the solution is divergent. Furthermore, for a given  , this is the unique solution going through
, this is the unique solution going through 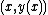 .
.
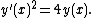
A one-parameter family of solutions to this equation is given by
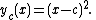
Another solution is given by
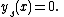
Since the equation being studied is a first-order equation, the initial conditions are the initial x and y values. By considering the two sets of solutions above, one can see that the solution fails to be unique when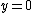 . (It can be shown that for
. (It can be shown that for  , if a single branch of the square root is chosen, then there is a local solution which is unique using the Picard–Lindelöf theorem
, if a single branch of the square root is chosen, then there is a local solution which is unique using the Picard–Lindelöf theorem
.) Thus, the solutions above are all singular solutions, in the sense that solution fails to be unique in a neighbourhood of one or more points. (Commonly, we say "uniqueness fails" at these points.) For the first set of solutions, uniqueness fails at one point, , and for the second solution, uniqueness fails at every value of
, and for the second solution, uniqueness fails at every value of  . Thus, the solution
. Thus, the solution 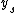 is a singular solution in the stronger sense that uniqueness fails at every value of x. However, it is not a singular function
is a singular solution in the stronger sense that uniqueness fails at every value of x. However, it is not a singular function
since it and all its derivatives are continuous.
In this example, the solution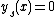 is the envelope of the family of solutions
is the envelope of the family of solutions  . The solution
. The solution 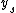 is tangent to every curve
is tangent to every curve 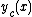 at the point
at the point 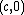 .
.
The failure of uniqueness can be used to construct more solutions. These can be found by taking two constant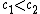 and defining a solution
and defining a solution 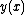 to be
to be 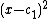 when
when 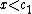 , to be
, to be  when
when 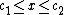 , and to be
, and to be 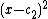 when
when  . Direct calculation shows that this is a solution of the differential equation at every point, including
. Direct calculation shows that this is a solution of the differential equation at every point, including 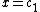 and
and  . Uniqueness fails for these solutions on the interval
. Uniqueness fails for these solutions on the interval 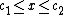 , and the solutions are singular, in the sense that the second derivative fails to exist, at
, and the solutions are singular, in the sense that the second derivative fails to exist, at 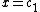 and
and  .
.
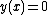 . Failure of uniqueness can also be seen in the following example of a Clairaut's equation:
. Failure of uniqueness can also be seen in the following example of a Clairaut's equation:
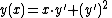
We write y' = p and then
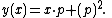
Now, we shall take the differential according to x:
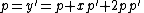
which by simple algebra
yields
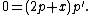
This condition is solved if 2p+x=0 or if p'=0.
If p' = 0 it means that y' = p = c = constant, and the general solution of this new equation is:
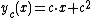
where c is determined by the initial value.
If x + 2p = 0 than we get that p = −(1/2)x and substituting in the ODE gives
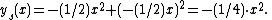
Now we shall check when these solutions are singular solutions. If two solutions intersect each other, that is, they both go through the same point (x,y), then there is a failure of uniqueness for a first-order ordinary differential equation. Thus, there will be a failure of uniqueness if a solution of the first form intersects the second solution.
The condition of intersection is : ys(x) = yc(x). We solve
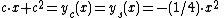
to find the intersection point, which is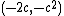 .
.
We can verify that the curves are tangent at this point y's(x) = y'c(x). We calculate the derivative
s:
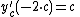

Hence,
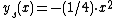
is tangent to every member of the one-parameter family of solutions

of this Clairaut equation:

Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
is a solution that is singular
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
or one for which the initial value problem
Initial value problem
In mathematics, in the field of differential equations, an initial value problem is an ordinary differential equation together with a specified value, called the initial condition, of the unknown function at a given point in the domain of the solution...
(also called the Cauchy problem by some authors) fails to have a unique solution at some point on the solution. The set on which a solution is singular may be as small as a single point or as large as the full real line. Solutions which are singular in the sense that the initial value problem fails to have a unique solution need not be singular functions
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
.
In some cases, the term singular solution is used to mean a solution at which there is a failure of uniqueness to the initial value problem at every point on the curve. A singular solution in this stronger sense is often given as tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to every solution from a family of solutions. By tangent we mean that there is a point x where ys(x) = yc(x) and y's(x) = y'c(x) where yc is a solution in a family of solutions parameterized by c. This means that the singular solution is the envelope
Envelope (mathematics)
In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves...
of the family of solutions.
Usually, singular solutions appear in differential equations when there is a need to divide in a term that might be equal to zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
. Therefore, when one is solving a differential equation and using division one must check what happens if the term is equal to zero, and whether it leads to a singular solution. The Picard–Lindelöf theorem
Picard–Lindelöf theorem
In mathematics, in the study of differential equations, the Picard–Lindelöf theorem, Picard's existence theorem or Cauchy–Lipschitz theorem is an important theorem on existence and uniqueness of solutions to first-order equations with given initial conditions.The theorem is named after Charles...
, which gives sufficient conditions for unique solutions to exist, can be used to rule out the existence of singular solutions. Other theorems, such as the Peano existence theorem
Peano existence theorem
In mathematics, specifically in the study of ordinary differential equations, the Peano existence theorem, Peano theorem or Cauchy-Peano theorem, named after Giuseppe Peano and Augustin Louis Cauchy, is a fundamental theorem which guarantees the existence of solutions to certain initial value...
, give sufficient conditions for solutions to exist with out necessarily being unique, which can allow for the existence of singular solutions.
A divergent solution
Consider the homogeneous linear ordinary differential
where primes denote derivatives with respect to x. The general solution to this equation is
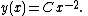
For a given
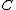 , this solution is smooth except at
, this solution is smooth except at 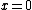 where the solution is divergent. Furthermore, for a given
where the solution is divergent. Furthermore, for a given  , this is the unique solution going through
, this is the unique solution going through 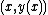 .
.Failure of uniqueness
Consider the differential equation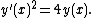
A one-parameter family of solutions to this equation is given by
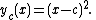
Another solution is given by
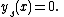
Since the equation being studied is a first-order equation, the initial conditions are the initial x and y values. By considering the two sets of solutions above, one can see that the solution fails to be unique when
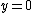 . (It can be shown that for
. (It can be shown that for  , if a single branch of the square root is chosen, then there is a local solution which is unique using the Picard–Lindelöf theorem
, if a single branch of the square root is chosen, then there is a local solution which is unique using the Picard–Lindelöf theoremPicard–Lindelöf theorem
In mathematics, in the study of differential equations, the Picard–Lindelöf theorem, Picard's existence theorem or Cauchy–Lipschitz theorem is an important theorem on existence and uniqueness of solutions to first-order equations with given initial conditions.The theorem is named after Charles...
.) Thus, the solutions above are all singular solutions, in the sense that solution fails to be unique in a neighbourhood of one or more points. (Commonly, we say "uniqueness fails" at these points.) For the first set of solutions, uniqueness fails at one point,
 , and for the second solution, uniqueness fails at every value of
, and for the second solution, uniqueness fails at every value of  . Thus, the solution
. Thus, the solution 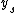 is a singular solution in the stronger sense that uniqueness fails at every value of x. However, it is not a singular function
is a singular solution in the stronger sense that uniqueness fails at every value of x. However, it is not a singular functionMathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
since it and all its derivatives are continuous.
In this example, the solution
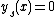 is the envelope of the family of solutions
is the envelope of the family of solutions  . The solution
. The solution 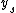 is tangent to every curve
is tangent to every curve 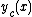 at the point
at the point 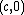 .
.The failure of uniqueness can be used to construct more solutions. These can be found by taking two constant
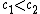 and defining a solution
and defining a solution 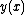 to be
to be 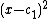 when
when 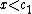 , to be
, to be  when
when 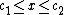 , and to be
, and to be 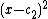 when
when  . Direct calculation shows that this is a solution of the differential equation at every point, including
. Direct calculation shows that this is a solution of the differential equation at every point, including 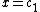 and
and  . Uniqueness fails for these solutions on the interval
. Uniqueness fails for these solutions on the interval 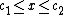 , and the solutions are singular, in the sense that the second derivative fails to exist, at
, and the solutions are singular, in the sense that the second derivative fails to exist, at 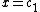 and
and  .
.Further example of failure of uniqueness
The previous example might give the erroneous impression that failure of uniqueness is directly related to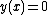 . Failure of uniqueness can also be seen in the following example of a Clairaut's equation:
. Failure of uniqueness can also be seen in the following example of a Clairaut's equation: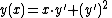
We write y' = p and then
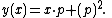
Now, we shall take the differential according to x:
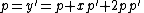
which by simple algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
yields
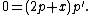
This condition is solved if 2p+x=0 or if p'=0.
If p' = 0 it means that y' = p = c = constant, and the general solution of this new equation is:
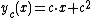
where c is determined by the initial value.
If x + 2p = 0 than we get that p = −(1/2)x and substituting in the ODE gives
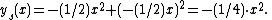
Now we shall check when these solutions are singular solutions. If two solutions intersect each other, that is, they both go through the same point (x,y), then there is a failure of uniqueness for a first-order ordinary differential equation. Thus, there will be a failure of uniqueness if a solution of the first form intersects the second solution.
The condition of intersection is : ys(x) = yc(x). We solve
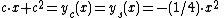
to find the intersection point, which is
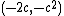 .
.We can verify that the curves are tangent at this point y's(x) = y'c(x). We calculate the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s:
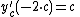

Hence,
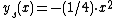
is tangent to every member of the one-parameter family of solutions

of this Clairaut equation:

See also
- Envelope (mathematics)Envelope (mathematics)In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves...
- Caustic (mathematics)Caustic (mathematics)In differential geometry and geometric optics, a caustic is the envelope of rays either reflected or refracted by a manifold. It is related to the optical concept of caustics...
- Initial value problemInitial value problemIn mathematics, in the field of differential equations, an initial value problem is an ordinary differential equation together with a specified value, called the initial condition, of the unknown function at a given point in the domain of the solution...
- Picard–Lindelöf theoremPicard–Lindelöf theoremIn mathematics, in the study of differential equations, the Picard–Lindelöf theorem, Picard's existence theorem or Cauchy–Lipschitz theorem is an important theorem on existence and uniqueness of solutions to first-order equations with given initial conditions.The theorem is named after Charles...

