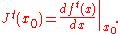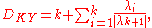Lyapunov exponent
Encyclopedia
In mathematics the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system
is a quantity that characterizes the rate of separation of infinitesimally close trajectories
. Quantitatively, two trajectories in phase space
with initial separation diverge (provided that the divergence can be treated within the linearized approximation)
diverge (provided that the divergence can be treated within the linearized approximation)

where is the Lyapunov exponent.
is the Lyapunov exponent.
The rate of separation can be different for different orientations of initial separation vector. Thus, there is a spectrum of Lyapunov exponents— equal in number to the dimensionality of the phase space. It is common to refer to the largest one as the Maximal Lyapunov exponent (MLE), because it determines a notion of predictability
for a dynamical system. A positive MLE is usually taken as an indication that the system is chaotic (provided some other conditions are met, e.g., phase space compactness). Note that an arbitrary initial separation vector will typically contain some component in the direction associated with the MLE, and because of the exponential growth rate, the effect of the other exponents will be obliterated over time.
The exponent is named after Aleksandr Lyapunov
.
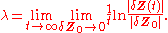
The limit ensures the validity of the linear approximation
ensures the validity of the linear approximation
at any time
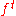 in an n–dimensional phase space, the spectrum of Lyapunov exponents
in an n–dimensional phase space, the spectrum of Lyapunov exponents
in general, depends on the starting point . (However, we will usually be interested in the attractor
. (However, we will usually be interested in the attractor
(or attractors) of a dynamical system, and there will normally be one set of exponents associated with each attractor. The choice of starting point may determine which attractor the system ends up on, if there is more than one. Note: Hamiltonian systems do not have attractors, so this particular discussion does not apply to them.) The Lyapunov exponents describe the behavior of vectors in the tangent space of the phase space and are defined from the Jacobian matrix
The matrix describes how a small change at the point
matrix describes how a small change at the point  propagates to the final point
propagates to the final point 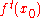 . The limit
. The limit
defines a matrix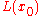 (the conditions for the existence of the limit are given by the Oseledec theorem
(the conditions for the existence of the limit are given by the Oseledec theorem
). If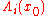 are the eigenvalues of
are the eigenvalues of  , then the Lyapunov exponents
, then the Lyapunov exponents 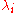 are defined by
are defined by
The set of Lyapunov exponents will be the same for almost all starting points of an ergodic component of the dynamical system.
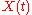
(e.g., for linearization along stationary solution in continuous system the funadamental matrix is
in continuous system the funadamental matrix is
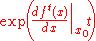 ),
),
consisting of the linear-independent solutions of the first approximation system.
The singular values
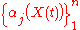
of the matrix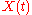 are the square roots of the eigenvalues of the matrix
are the square roots of the eigenvalues of the matrix 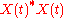 .
.
The largest Lyapunov exponent is as follows
is as follows

A.M. Lyapunov
proved that if the system of the first approximation is regular (e.g., all systems with constant and periodic coefficients are regular) and its largest Lyapunov exponent is negative, then the solution of the original system is asymptotically Lyapunov stable
.
Later, it was stated by O. Perron that the requirement of regularity of the first approximation is substantial.
is Lyapunov stable.
The effect of sign inversion of Lyapunov exponents of solutions of the original system and the system of first approximation with the same initial data was subsequently
called the Perron effect.
So, counterexample of Perron shows that positive largest Lyapunov exponent doesn't, in general, indicate chaos and negative largest Lyapunov exponent doesn't, in general, indicate stability.
Therefore time-varying linearization requires additional justification.
), a volume element of the phase space will stay the same along a trajectory. Thus the sum of all Lyapunov exponents must be zero. If the system is dissipative, the sum of Lyapunov exponents is negative.
If the system is a flow and the trajectory does not converge to a single point, one exponent is always zero—the Lyapunov exponent corresponding to the eigenvalue of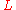 with an eigenvector in the direction of the flow.
with an eigenvector in the direction of the flow.
and of the fractal dimension
of the considered dynamical system
. In particular from the knowledge
of the Lyapunov spectrum it is possible to obtain the so-called Kaplan–Yorke dimension , that is defined as follows:
, that is defined as follows:
where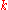 is the maximum integer such that the sum of the
is the maximum integer such that the sum of the 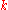 largest exponents is still non-negative.
largest exponents is still non-negative. 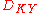 represents an upper bound for the information dimension of the system. Moreover, the sum of all the positive Lyapunov exponents gives an estimate of the Kolmogorov–Sinai entropy accordingly to Pesin's theorem.
represents an upper bound for the information dimension of the system. Moreover, the sum of all the positive Lyapunov exponents gives an estimate of the Kolmogorov–Sinai entropy accordingly to Pesin's theorem.
The multiplicative inverse
of the largest Lyapunov exponent is sometimes referred in literature as Lyapunov time
, and defines the characteristic e-folding time. For chaotic orbits, the Lyapunov time will be finite, whereas for regular orbits it will be infinite.
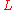 matrix based on averaging several finite time approximations of the limit defining
matrix based on averaging several finite time approximations of the limit defining  .
.
One of the most used and effective numerical techniques to calculate the Lyapunov spectrum for a smooth dynamical system relies on periodic
Gram–Schmidt orthonormalization of the Lyapunov vector
s to avoid a misalignment of all the vectors along the direction of maximal expansion.I. Shimada and T. Nagashima, Prog. Theor. Phys. 61, 1605 (1979).
For the calculation of Lyapunov exponents from limited experimental data, various methods have been proposed. However, there are many difficulties with applying these methods and such problems should be approached with care.
, in which there are two systems that are coupled, usually in a unidirectional manner so that there is a drive (or master) system and a response (or slave) system. The conditional exponents are those of the response system with the drive system treated as simply the source of a (chaotic) drive signal. Synchronization occurs when all of the conditional exponents are negative.
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
is a quantity that characterizes the rate of separation of infinitesimally close trajectories
Trajectory
A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...
. Quantitatively, two trajectories in phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
with initial separation
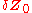 diverge (provided that the divergence can be treated within the linearized approximation)
diverge (provided that the divergence can be treated within the linearized approximation)
where
 is the Lyapunov exponent.
is the Lyapunov exponent.The rate of separation can be different for different orientations of initial separation vector. Thus, there is a spectrum of Lyapunov exponents— equal in number to the dimensionality of the phase space. It is common to refer to the largest one as the Maximal Lyapunov exponent (MLE), because it determines a notion of predictability
Predictability
Predictability is the degree to which a correct prediction or forecast of a system's state can be made either qualitatively or quantitatively.-Predictability and Causality:...
for a dynamical system. A positive MLE is usually taken as an indication that the system is chaotic (provided some other conditions are met, e.g., phase space compactness). Note that an arbitrary initial separation vector will typically contain some component in the direction associated with the MLE, and because of the exponential growth rate, the effect of the other exponents will be obliterated over time.
The exponent is named after Aleksandr Lyapunov
Aleksandr Lyapunov
Aleksandr Mikhailovich Lyapunov was a Russian mathematician, mechanician and physicist. His surname is sometimes romanized as Ljapunov, Liapunov or Ljapunow....
.
Definition of the maximal Lyapunov exponent
The maximal Lyapunov exponent can be defined as follows: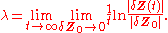
The limit
 ensures the validity of the linear approximation
ensures the validity of the linear approximationat any time
Definition of the Lyapunov spectrum
For a dynamical system with evolution equation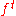 in an n–dimensional phase space, the spectrum of Lyapunov exponents
in an n–dimensional phase space, the spectrum of Lyapunov exponentsin general, depends on the starting point
 . (However, we will usually be interested in the attractor
. (However, we will usually be interested in the attractorAttractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
(or attractors) of a dynamical system, and there will normally be one set of exponents associated with each attractor. The choice of starting point may determine which attractor the system ends up on, if there is more than one. Note: Hamiltonian systems do not have attractors, so this particular discussion does not apply to them.) The Lyapunov exponents describe the behavior of vectors in the tangent space of the phase space and are defined from the Jacobian matrix
The
 matrix describes how a small change at the point
matrix describes how a small change at the point  propagates to the final point
propagates to the final point 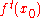 . The limit
. The limitdefines a matrix
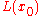 (the conditions for the existence of the limit are given by the Oseledec theorem
(the conditions for the existence of the limit are given by the Oseledec theoremOseledec theorem
In mathematics, the multiplicative ergodic theorem, or Oseledets theorem provides the theoretical background for computation of Lyapunov exponents of a nonlinear dynamical system. It was proved by Valery Oseledets in 1965 and reported at the International Mathematical Congress in Moscow in 1966...
). If
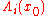 are the eigenvalues of
are the eigenvalues of  , then the Lyapunov exponents
, then the Lyapunov exponents 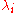 are defined by
are defined byThe set of Lyapunov exponents will be the same for almost all starting points of an ergodic component of the dynamical system.
Lyapunov exponent for time-varying linearization
To introduce Lyapunov exponent let us consider a fundamental matrix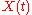
(e.g., for linearization along stationary solution
 in continuous system the funadamental matrix is
in continuous system the funadamental matrix is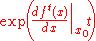 ),
),consisting of the linear-independent solutions of the first approximation system.
The singular values
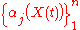
of the matrix
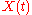 are the square roots of the eigenvalues of the matrix
are the square roots of the eigenvalues of the matrix 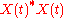 .
.The largest Lyapunov exponent
 is as follows
is as follows
A.M. Lyapunov
Aleksandr Lyapunov
Aleksandr Mikhailovich Lyapunov was a Russian mathematician, mechanician and physicist. His surname is sometimes romanized as Ljapunov, Liapunov or Ljapunow....
proved that if the system of the first approximation is regular (e.g., all systems with constant and periodic coefficients are regular) and its largest Lyapunov exponent is negative, then the solution of the original system is asymptotically Lyapunov stable
Lyapunov stability
Various types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
.
Later, it was stated by O. Perron that the requirement of regularity of the first approximation is substantial.
Perron effects of largest Lyapunov exponent sign inversion
In 1930 O. Perron constructed an example of the second-order system, the first approximation of which has negative Lyapunov exponents along a zero solution of the original system but, at the same time, this zero solution of original nonlinear system is Lyapunov unstable. Furthermore, in a certain neighborhood of this zero solution almost all solutions of original system have positive Lyapunov exponents. Also it is possible to construct reverse example when first approximation has positive Lyapunov exponents along a zero solution of the original system but, at the same time, this zero solution of original nonlinear systemis Lyapunov stable.
The effect of sign inversion of Lyapunov exponents of solutions of the original system and the system of first approximation with the same initial data was subsequently
called the Perron effect.
So, counterexample of Perron shows that positive largest Lyapunov exponent doesn't, in general, indicate chaos and negative largest Lyapunov exponent doesn't, in general, indicate stability.
Therefore time-varying linearization requires additional justification.
Basic properties
If the system is conservative (i.e. there is no dissipationDissipation
In physics, dissipation embodies the concept of a dynamical system where important mechanical models, such as waves or oscillations, lose energy over time, typically from friction or turbulence. The lost energy converts into heat, which raises the temperature of the system. Such systems are called...
), a volume element of the phase space will stay the same along a trajectory. Thus the sum of all Lyapunov exponents must be zero. If the system is dissipative, the sum of Lyapunov exponents is negative.
If the system is a flow and the trajectory does not converge to a single point, one exponent is always zero—the Lyapunov exponent corresponding to the eigenvalue of
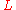 with an eigenvector in the direction of the flow.
with an eigenvector in the direction of the flow.Significance of the Lyapunov spectrum
The Lyapunov spectrum can be used to give an estimate of the rate of entropy productionand of the fractal dimension
Fractal dimension
In fractal geometry, the fractal dimension, D, is a statistical quantity that gives an indication of how completely a fractal appears to fill space, as one zooms down to finer and finer scales. There are many specific definitions of fractal dimension. The most important theoretical fractal...
of the considered dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
. In particular from the knowledge
of the Lyapunov spectrum it is possible to obtain the so-called Kaplan–Yorke dimension
 , that is defined as follows:
, that is defined as follows:where
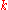 is the maximum integer such that the sum of the
is the maximum integer such that the sum of the 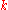 largest exponents is still non-negative.
largest exponents is still non-negative. 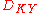 represents an upper bound for the information dimension of the system. Moreover, the sum of all the positive Lyapunov exponents gives an estimate of the Kolmogorov–Sinai entropy accordingly to Pesin's theorem.
represents an upper bound for the information dimension of the system. Moreover, the sum of all the positive Lyapunov exponents gives an estimate of the Kolmogorov–Sinai entropy accordingly to Pesin's theorem.The multiplicative inverse
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of the largest Lyapunov exponent is sometimes referred in literature as Lyapunov time
Lyapunov time
In mathematics, the Lyapunov time is the length of time for a dynamical system to become chaotic. The Lyapunov time reflects the limits of the predictability of the system. By convention, it is defined as the time for the distance between nearby trajectories of the system to increase by a factor...
, and defines the characteristic e-folding time. For chaotic orbits, the Lyapunov time will be finite, whereas for regular orbits it will be infinite.
Numerical calculation
Generally the calculation of Lyapunov exponents, as defined above, cannot be carried out analytically, and in most cases one must resort to numerical techniques. An early example, which also constituted the first demonstration of the exponential divergence of chaotic trajectories, was carried out by R. H. Miller in 1964. Currently, the most commonly used numerical procedure estimates the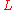 matrix based on averaging several finite time approximations of the limit defining
matrix based on averaging several finite time approximations of the limit defining  .
.One of the most used and effective numerical techniques to calculate the Lyapunov spectrum for a smooth dynamical system relies on periodic
Gram–Schmidt orthonormalization of the Lyapunov vector
Lyapunov vector
In applied mathematics and dynamical system theory, Lyapunov vectors, named after Aleksandr Lyapunov, describe characteristic expanding and contracting directions of a dynamical system. They have been used in predictability analysis and as initial perturbations for ensemble forecasting in numerical...
s to avoid a misalignment of all the vectors along the direction of maximal expansion.I. Shimada and T. Nagashima, Prog. Theor. Phys. 61, 1605 (1979).
For the calculation of Lyapunov exponents from limited experimental data, various methods have been proposed. However, there are many difficulties with applying these methods and such problems should be approached with care.
Local Lyapunov exponent
Whereas the (global) Lyapunov exponent gives a measure for the total predictability of a system, it is sometimes interesting to estimate the local predictability around a point x0 in phase space. This may be done through the eigenvalues of the Jacobian matrix J 0(x0). These eigenvalues are also called local Lyapunov exponents. (A word of caution: unlike the global exponents, these local exponents are not invariant under a nonlinear change of coordinates.)Conditional Lyapunov exponent
This term is normally used in regards to the synchronization of chaosSynchronization of chaos
Synchronization of chaos is a phenomenon that may occur when two, or more, chaotic oscillators are coupled, or when a chaotic oscillator drives another chaotic oscillator...
, in which there are two systems that are coupled, usually in a unidirectional manner so that there is a drive (or master) system and a response (or slave) system. The conditional exponents are those of the response system with the drive system treated as simply the source of a (chaotic) drive signal. Synchronization occurs when all of the conditional exponents are negative.
See also
- Aleksandr LyapunovAleksandr LyapunovAleksandr Mikhailovich Lyapunov was a Russian mathematician, mechanician and physicist. His surname is sometimes romanized as Ljapunov, Liapunov or Ljapunow....
- Oseledec theoremOseledec theoremIn mathematics, the multiplicative ergodic theorem, or Oseledets theorem provides the theoretical background for computation of Lyapunov exponents of a nonlinear dynamical system. It was proved by Valery Oseledets in 1965 and reported at the International Mathematical Congress in Moscow in 1966...
- Liouville's theorem (Hamiltonian)Liouville's theorem (Hamiltonian)In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
- Floquet theory
- Recurrence quantification analysisRecurrence quantification analysisRecurrence quantification analysis is a method of nonlinear data analysis for the investigation of dynamical systems. It quantifies the number and duration of recurrences of a dynamical system presented by its phase space trajectory....
Further reading
- Cvitanović P., Artuso R., Mainieri R. , Tanner G. and Vattay G.Chaos: Classical and Quantum Niels Bohr Institute, Copenhagen 2005 – textbook about chaos available under Free Documentation License
Software
- http://www.mpipks-dresden.mpg.de/~tisean/Tisean_3.0.1/index.html R. Hegger, H. Kantz, and T. Schreiber, Nonlinear Time Series Analysis, TISEANTiseanTISEAN is a software package for the analysis of time series with methods based on the theory of nonlinear dynamical systems. It was developed by Rainer Hegger, Holger Kantz and Thomas Schreiber and is distributed under the GPL licence...
3.0.1 (March 2007). - http://www.Scientio.com/Products/ChaosKit Scientio's ChaosKit product calculates Lyapunov exponents amongst other Chaotic measures. Access is provided online via a web service and Silverlight demo .
- [ftp://ftp2.sco.com/pub/skunkware/src/x11/misc/mathrec-1.1c.tar.gz] Dr. Ronald Joe Record's mathematical recreations software laboratory includes an X11 graphical client, lyap, for graphically exploring the Lyapunov exponents of a forced logistic map and other maps of the unit interval. The [ftp://ftp2.sco.com/pub/skunkware/src/x11/misc/mathrec-1.1c/ReadMe.html contents and manual pages] of the mathrec software laboratory are also available.
- http://inls.ucsd.edu/~pbryant/ On this web page is software called LyapOde, which includes source code written in "C" for calculation of Lyapunov exponents when the differential equations are known. It can also calculate the conditional Lyapunov exponents for coupled identical systems. The software can be compiled for running on Windows, Mac, or Linux/Unix systems. It includes the equations for several systems (Lorenz, Rossler, etc.) and documentation on how to create and compile software for additional systems of the user's choice. The software runs in a text window and has no graphics capabilities, but it is efficient and has no inherent limitations on the number of variables etc. It uses the QR decomposition method of Eckmann and Ruelle (Reviews of Modern Physics, Vol. 57, No. 3, Part1, (1985), 617).