
Mixing (mathematics)
Encyclopedia
In mathematics
, mixing is an abstract concept originating from physics
: the attempt to describe the irreversible thermodynamic process of mixing
in the everyday world: mixing paint, mixing drinks, etc.
The concept appears in ergodic theory
—the study of stochastic process
es and measure-preserving dynamical system
s. Several different definitions for mixing exist, including strong mixing, weak mixing and topological mixing, with the last not requiring a measure
to be defined. Some of the different definitions of mixing can be arranged in a hierarchical order; thus, strong mixing implies weak mixing. Furthermore, weak mixing (and thus also strong mixing) implies ergodicity
: that is, every system that is weakly mixing is also ergodic (and so one says that mixing is a "stronger" notion than ergodicity).
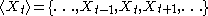 be a sequence of random variable
be a sequence of random variable
s. Such a sequence is naturally endowed with a topology, the product topology
. The open set
s of this topology are called cylinder set
s. These cylinder sets generate a sigma algebra, the Borel sigma algebra; it is the smallest (coarsest) sigma algebra that contains the topology.
Define a function , called the strong mixing coefficient, as
, called the strong mixing coefficient, as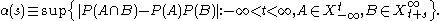
In this definition, P is the probability measure
on the sigma algebra. The symbol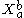 , with
, with 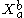 denotes a subalgebra of the sigma algebra; it is the set of cylinder sets that are specified between times a and b. Given specific, fixed values
denotes a subalgebra of the sigma algebra; it is the set of cylinder sets that are specified between times a and b. Given specific, fixed values 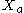 ,
, 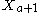 , etc., of the random variable, at times
, etc., of the random variable, at times  ,
,  , etc., then it may be thought of as the sigma-algebra
, etc., then it may be thought of as the sigma-algebra
generated by
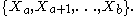
The process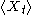 is strong mixing if
is strong mixing if 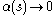 as
as  .
.
One way to describe this is that strong mixing implies that for any two possible states of the system (realizations of the random variable), when given a sufficient amount of time between the two states, the occurrence of the states is independent
.
, with stationary distribution Q. Denote L²(Q) the space of Borel-measurable functions that are square-integrable with respect to measure Q. Also let denote the conditional expectation operator on L²(Q). Finally, let } denote the space of square-integrable functions with mean zero.
The ρ-mixing coefficients of the process {xt} are
The α-mixing coefficients of the process {xt} are
The α-mixing coefficients are always smaller than the ρ-mixing ones: , therefore if the process is ρ-mixing, it will necessarily be α-mixing too. However when , the process may still be α-mixing, with sub-exponential decay rate.
The β-mixing coefficients are given by
A strictly stationary Markov process is β-mixing if and only if it is an aperiodic recurrent Harris chain. The β-mixing coefficients are always bigger than the α-mixing ones, so if a process is β-mixing it will also be α-mixing. There is no direct relationship between β-mixing and ρ-mixing: neither of them implies the other.
s. Let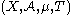 be a dynamical system, with T being the time-evolution or shift operator
be a dynamical system, with T being the time-evolution or shift operator
. The system is said to be strong mixing if, for any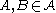 , one has
, one has
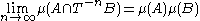 .
.
For shifts parametrized by a continuous variable instead of a discrete integer n, the same definition applies, with replaced by
replaced by 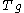 with g being the continuous-time parameter.
with g being the continuous-time parameter.
To understand the above definition physically, consider a shaker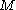 full of an incompressible liquid, which consists of 20% wine and 80% water. If
full of an incompressible liquid, which consists of 20% wine and 80% water. If 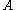 is the region originally occupied by the wine, then, for any part
is the region originally occupied by the wine, then, for any part 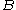 of the shaker, the percentage of wine in
of the shaker, the percentage of wine in 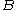 after n repetitions of the act of stirring is
after n repetitions of the act of stirring is
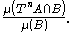
In such a situation, one would expect that after the liquid is sufficiently stirred (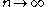 ), every part
), every part 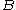 of the shaker will contain approximately 20% wine. This leads to
of the shaker will contain approximately 20% wine. This leads to
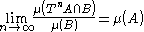
which implies the above definition of strong mixing.
A dynamical system is said to be weak mixing if one has
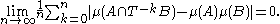
In other words,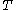 is strong mixing if
is strong mixing if  converges towards
converges towards 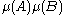 . and weak mixing if this convergence is only in the Cesàro sense).
. and weak mixing if this convergence is only in the Cesàro sense).
Weak mixing is a sufficient condition for ergodicity.
For a system that is weak mixing, the shift operator
T will have no (non-constant) square-integrable eigenfunction
s with associated eigenvalue of one. In general, a shift operator will have a continuous spectrum
, and thus will always have eigenfunctions that are generalized function
s. However, for the system to be (at least) weak mixing, none of the eigenfunctions with associated eigenvalue of one can be square integrable.
, only using the topology
of the system. A continuous map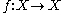 is said to be topologically transitive if, for every pair of non-empty open set
is said to be topologically transitive if, for every pair of non-empty open set
s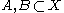 , there exists an integer n such that
, there exists an integer n such that

where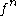 is the n 'th iterate
is the n 'th iterate
of f. In the operator theory
, a topologically transitive bounded linear operator (a continuous linear map on a topological vector space
) is usually called hypercyclic operator. A related idea is expressed by the wandering set
.
Lemma: If X is a compact
metric space
, then f is topologically transitive if and only if there exists a hypercyclic point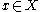 , that is, a point x such that its orbit
, that is, a point x such that its orbit 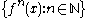 is dense
is dense
in X.
A system is said to be topologically mixing if, given sets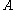 and
and 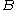 , there exists an integer N, such that, for all
, there exists an integer N, such that, for all 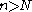 , one has
, one has
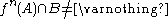 .
.
For a continuous-time system, is replaced by the flow
is replaced by the flow
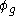 , with g being the continuous parameter, with the requirement that a non-empty intersection hold for all
, with g being the continuous parameter, with the requirement that a non-empty intersection hold for all  .
.
A weak topological mixing is one that has no non-constant continuous (with respect to the topology) eigenfunctions of the shift operator.
Topological mixing neither implies, nor is implied by either weak or strong mixing: there are examples of systems that are weak mixing but not topologically mixing, and examples that are topologically mixing but not strong mixing.
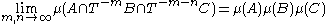
holds for all measurable sets A, B, C. We can define strong k-mixing similarly. A system which is strong k-mixing for all k=2,3,4,... is called mixing of all orders.
It is unknown whether strong 2-mixing implies strong 3-mixing. It is known that strong m-mixing implies ergodicity
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, mixing is an abstract concept originating from physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
: the attempt to describe the irreversible thermodynamic process of mixing
Mixing (physics)
In physics, a dynamical system is said to be mixing if the phase space of the system becomes strongly intertwined, according to at least one of several mathematical definitions. For example, a measure-preserving transformation T is said to be strong mixing ifwhenever A and B are any measurable...
in the everyday world: mixing paint, mixing drinks, etc.
The concept appears in ergodic theory
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
—the study of stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
es and measure-preserving dynamical system
Measure-preserving dynamical system
In mathematics, a measure-preserving dynamical system is an object of study in the abstract formulation of dynamical systems, and ergodic theory in particular.-Definition:...
s. Several different definitions for mixing exist, including strong mixing, weak mixing and topological mixing, with the last not requiring a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
to be defined. Some of the different definitions of mixing can be arranged in a hierarchical order; thus, strong mixing implies weak mixing. Furthermore, weak mixing (and thus also strong mixing) implies ergodicity
Ergodicity
In mathematics, the term ergodic is used to describe a dynamical system which, broadly speaking, has the same behavior averaged over time as averaged over space. In physics the term is used to imply that a system satisfies the ergodic hypothesis of thermodynamics.-Etymology:The word ergodic is...
: that is, every system that is weakly mixing is also ergodic (and so one says that mixing is a "stronger" notion than ergodicity).
Mixing in stochastic processes
Let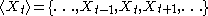 be a sequence of random variable
be a sequence of random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s. Such a sequence is naturally endowed with a topology, the product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
. The open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s of this topology are called cylinder set
Cylinder set
In mathematics, a cylinder set is the natural open set of a product topology. Cylinder sets are particularly useful in providing the base of the natural topology of the product of a countable number of copies of a set...
s. These cylinder sets generate a sigma algebra, the Borel sigma algebra; it is the smallest (coarsest) sigma algebra that contains the topology.
Define a function
 , called the strong mixing coefficient, as
, called the strong mixing coefficient, as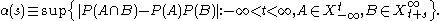
In this definition, P is the probability measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on the sigma algebra. The symbol
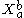 , with
, with 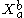 denotes a subalgebra of the sigma algebra; it is the set of cylinder sets that are specified between times a and b. Given specific, fixed values
denotes a subalgebra of the sigma algebra; it is the set of cylinder sets that are specified between times a and b. Given specific, fixed values 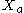 ,
, 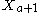 , etc., of the random variable, at times
, etc., of the random variable, at times  ,
,  , etc., then it may be thought of as the sigma-algebra
, etc., then it may be thought of as the sigma-algebraSigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
generated by
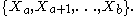
The process
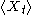 is strong mixing if
is strong mixing if 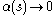 as
as  .
.One way to describe this is that strong mixing implies that for any two possible states of the system (realizations of the random variable), when given a sufficient amount of time between the two states, the occurrence of the states is independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
.
Types of mixing
Suppose {Xt} is a stationary Markov processMarkov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
, with stationary distribution Q. Denote L²(Q) the space of Borel-measurable functions that are square-integrable with respect to measure Q. Also let denote the conditional expectation operator on L²(Q). Finally, let } denote the space of square-integrable functions with mean zero.
The ρ-mixing coefficients of the process {xt} are
-
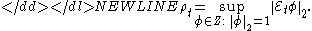
The process is called
The α-mixing coefficients of the process {xt} are
-
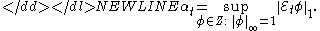
The process is called
The α-mixing coefficients are always smaller than the ρ-mixing ones: , therefore if the process is ρ-mixing, it will necessarily be α-mixing too. However when , the process may still be α-mixing, with sub-exponential decay rate.
The β-mixing coefficients are given by
-
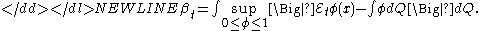
The process is called
A strictly stationary Markov process is β-mixing if and only if it is an aperiodic recurrent Harris chain. The β-mixing coefficients are always bigger than the α-mixing ones, so if a process is β-mixing it will also be α-mixing. There is no direct relationship between β-mixing and ρ-mixing: neither of them implies the other.
Mixing in dynamical systems
A similar definition can be given using the vocabulary of measure-preserving dynamical systemMeasure-preserving dynamical system
In mathematics, a measure-preserving dynamical system is an object of study in the abstract formulation of dynamical systems, and ergodic theory in particular.-Definition:...
s. Let
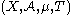 be a dynamical system, with T being the time-evolution or shift operator
be a dynamical system, with T being the time-evolution or shift operatorShift operator
In mathematics, and in particular functional analysis, the shift operator or translation operator is an operator that takes a function to its translation . In time series analysis, the shift operator is called the lag operator....
. The system is said to be strong mixing if, for any
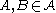 , one has
, one has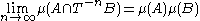 .
.For shifts parametrized by a continuous variable instead of a discrete integer n, the same definition applies, with
 replaced by
replaced by 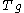 with g being the continuous-time parameter.
with g being the continuous-time parameter.To understand the above definition physically, consider a shaker
 full of an incompressible liquid, which consists of 20% wine and 80% water. If
full of an incompressible liquid, which consists of 20% wine and 80% water. If 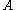 is the region originally occupied by the wine, then, for any part
is the region originally occupied by the wine, then, for any part 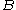 of the shaker, the percentage of wine in
of the shaker, the percentage of wine in 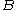 after n repetitions of the act of stirring is
after n repetitions of the act of stirring is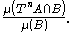
In such a situation, one would expect that after the liquid is sufficiently stirred (
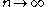 ), every part
), every part 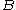 of the shaker will contain approximately 20% wine. This leads to
of the shaker will contain approximately 20% wine. This leads to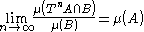
which implies the above definition of strong mixing.
A dynamical system is said to be weak mixing if one has
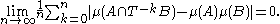
In other words,
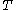 is strong mixing if
is strong mixing if  converges towards
converges towards 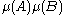 . and weak mixing if this convergence is only in the Cesàro sense).
. and weak mixing if this convergence is only in the Cesàro sense).Weak mixing is a sufficient condition for ergodicity.
For a system that is weak mixing, the shift operator
Shift operator
In mathematics, and in particular functional analysis, the shift operator or translation operator is an operator that takes a function to its translation . In time series analysis, the shift operator is called the lag operator....
T will have no (non-constant) square-integrable eigenfunction
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
s with associated eigenvalue of one. In general, a shift operator will have a continuous spectrum
Decomposition of spectrum (functional analysis)
In mathematics, especially functional analysis, the spectrum of an operator generalizes the notion of eigenvalues. Given an operator, it is sometimes useful to break up the spectrum into various parts...
, and thus will always have eigenfunctions that are generalized function
Generalized function
In mathematics, generalized functions are objects generalizing the notion of functions. There is more than one recognized theory. Generalized functions are especially useful in making discontinuous functions more like smooth functions, and describing physical phenomena such as point charges...
s. However, for the system to be (at least) weak mixing, none of the eigenfunctions with associated eigenvalue of one can be square integrable.
Topological mixing
A form of mixing may be defined without appeal to a measureMeasure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
, only using the topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
of the system. A continuous map
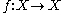 is said to be topologically transitive if, for every pair of non-empty open set
is said to be topologically transitive if, for every pair of non-empty open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s
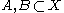 , there exists an integer n such that
, there exists an integer n such that
where
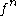 is the n 'th iterate
is the n 'th iterateIterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
of f. In the operator theory
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, a topologically transitive bounded linear operator (a continuous linear map on a topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
) is usually called hypercyclic operator. A related idea is expressed by the wandering set
Wandering set
In those branches of mathematics called dynamical systems and ergodic theory, the concept of a wandering set formalizes a certain idea of movement and mixing in such systems. When a dynamical system has a wandering set of non-zero measure, then the system is a dissipative system...
.
Lemma: If X is a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, then f is topologically transitive if and only if there exists a hypercyclic point
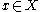 , that is, a point x such that its orbit
, that is, a point x such that its orbit 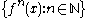 is dense
is denseDense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
in X.
A system is said to be topologically mixing if, given sets
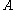 and
and 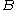 , there exists an integer N, such that, for all
, there exists an integer N, such that, for all 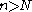 , one has
, one has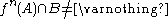 .
.For a continuous-time system,
 is replaced by the flow
is replaced by the flowFlow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
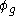 , with g being the continuous parameter, with the requirement that a non-empty intersection hold for all
, with g being the continuous parameter, with the requirement that a non-empty intersection hold for all  .
.A weak topological mixing is one that has no non-constant continuous (with respect to the topology) eigenfunctions of the shift operator.
Topological mixing neither implies, nor is implied by either weak or strong mixing: there are examples of systems that are weak mixing but not topologically mixing, and examples that are topologically mixing but not strong mixing.
Generalizations
The definition given above is sometimes called strong 2-mixing, to distinguish it from higher orders of mixing. A strong 3-mixing system may be defined as a system for which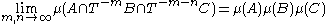
holds for all measurable sets A, B, C. We can define strong k-mixing similarly. A system which is strong k-mixing for all k=2,3,4,... is called mixing of all orders.
It is unknown whether strong 2-mixing implies strong 3-mixing. It is known that strong m-mixing implies ergodicity
Ergodicity
In mathematics, the term ergodic is used to describe a dynamical system which, broadly speaking, has the same behavior averaged over time as averaged over space. In physics the term is used to imply that a system satisfies the ergodic hypothesis of thermodynamics.-Etymology:The word ergodic is...
.

