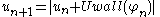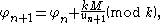Fermi–Ulam model
Encyclopedia
The Fermi–Ulam model (FUM) is a dynamical system
that was introduced by Polish
mathematician
Stanislaw Ulam in 1961.
FUM is a variant of Enrico Fermi's
primary work on acceleration of cosmic ray
s, namely Fermi acceleration
. The system consists of a particle that collides elastically between a fixed wall and a moving one, of infinite mass each. The walls represent the magnetic mirror
s with whom the cosmic particles collide.
A. J. Lichtenberg and M. A. Lieberman provided a simplified version of FUM (SFUM) that derives from the
Poincaré surface of section
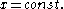and writes
where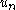
is the velocity of the particle after the 
-th collision with the fixed wall, 
is the corresponding phase of the moving wall,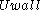 
is the velocity law of the moving wall and 
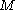is the stochasticity parameter of the system.
If the velocity law of the moving wall is differentiable enough, according to KAM theorem
invariant curves in the phase space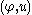
exist. These invariant curves act as barriers that do not allow for a particle to further accelerate and the average velocity of a population of particles saturates after finite iterations of the map. For instance, for sinusoidal velocity law of the moving wall such curves exist, while they do not for sawtooth velocity law that is discontinuous. Consequently, at the first case particles cannot accelerate infinitely, reversely to what happens at the last one.
FUM became over the years a prototype model for studying non-linear dynamics and coupled mappings
.
The rigorous solution of the Fermi-Ulam problem (the velocity and energy of the particle are bounded) was given first by L. D. Pustyl'nikov in (see also and references therein).
In spite of these negative results, if one considers the Fermi–Ulam model in the framework of the special theory of relativity, then under some general conditions the energy of the particle tends to infinity for an open set of initial data .
with oscillating boundaries ,,. The growth rate of energy in chaotic
billiards is found to be much larger than that in billiards that are integrable
in the static limit.
Strongly chaotic billiard with oscillating boundary can serve as a paradigm for driven chaotic systems.
In the experimental arena this topic arises in the theory of nuclear friction
,
and more recently in the studies of cold atoms that are trapped in optical billiards
.
The driving induces diffusion in energy
,
and consequently the absorption coefficient is determined by the Kubo formula
.
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
that was introduced by Polish
Poland
Poland , officially the Republic of Poland , is a country in Central Europe bordered by Germany to the west; the Czech Republic and Slovakia to the south; Ukraine, Belarus and Lithuania to the east; and the Baltic Sea and Kaliningrad Oblast, a Russian exclave, to the north...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Stanislaw Ulam in 1961.
FUM is a variant of Enrico Fermi's
Enrico Fermi
Enrico Fermi was an Italian-born, naturalized American physicist particularly known for his work on the development of the first nuclear reactor, Chicago Pile-1, and for his contributions to the development of quantum theory, nuclear and particle physics, and statistical mechanics...
primary work on acceleration of cosmic ray
Cosmic ray
Cosmic rays are energetic charged subatomic particles, originating from outer space. They may produce secondary particles that penetrate the Earth's atmosphere and surface. The term ray is historical as cosmic rays were thought to be electromagnetic radiation...
s, namely Fermi acceleration
Fermi acceleration
Fermi acceleration , sometimes referred to as diffusive shock acceleration , is the acceleration that charged particles undergo when being repeatedly reflected, usually by a magnetic mirror. This is thought to be the primary mechanism by which particles gain non thermal energies in astrophysical...
. The system consists of a particle that collides elastically between a fixed wall and a moving one, of infinite mass each. The walls represent the magnetic mirror
Magnetic mirror
A magnetic mirror is a magnetic field configuration where the field strength changes when moving along a field line. The mirror effect results in a tendency for charged particles to bounce back from the high field region....
s with whom the cosmic particles collide.
A. J. Lichtenberg and M. A. Lieberman provided a simplified version of FUM (SFUM) that derives from the
Poincaré surface of section
Poincaré map
In mathematics, particularly in dynamical systems, a first recurrence map or Poincaré map, named after Henri Poincaré, is the intersection of a periodic orbit in the state space of a continuous dynamical system with a certain lower dimensional subspace, called the Poincaré section, transversal to...
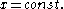and writes
where
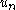is the velocity of the particle after the -th collision with the fixed wall, is the corresponding phase of the moving wall, 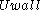is the velocity law of the moving wall and 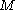is the stochasticity parameter of the system.If the velocity law of the moving wall is differentiable enough, according to KAM theorem
Kolmogorov–Arnold–Moser theorem
The Kolmogorov–Arnold–Moser theorem is a result in dynamical systems about the persistence of quasi-periodic motions under small perturbations. The theorem partly resolves the small-divisor problem that arises in the perturbation theory of classical mechanics....
invariant curves in the phase space
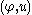exist. These invariant curves act as barriers that do not allow for a particle to further accelerate and the average velocity of a population of particles saturates after finite iterations of the map. For instance, for sinusoidal velocity law of the moving wall such curves exist, while they do not for sawtooth velocity law that is discontinuous. Consequently, at the first case particles cannot accelerate infinitely, reversely to what happens at the last one.FUM became over the years a prototype model for studying non-linear dynamics and coupled mappings
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
.
The rigorous solution of the Fermi-Ulam problem (the velocity and energy of the particle are bounded) was given first by L. D. Pustyl'nikov in (see also and references therein).
In spite of these negative results, if one considers the Fermi–Ulam model in the framework of the special theory of relativity, then under some general conditions the energy of the particle tends to infinity for an open set of initial data .
2D Generalization
Though the 1D FUM does not lead to acceleration for smooth oscillations, unbounded energy growth has been observed in 2D billiardsDynamical billiards
A billiard is a dynamical system in which a particle alternates between motion in a straight line and specular reflections from a boundary. When the particle hits the boundary it reflects from it without loss of speed...
with oscillating boundaries ,,. The growth rate of energy in chaotic
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
billiards is found to be much larger than that in billiards that are integrable
Integrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
in the static limit.
Strongly chaotic billiard with oscillating boundary can serve as a paradigm for driven chaotic systems.
In the experimental arena this topic arises in the theory of nuclear friction
,
and more recently in the studies of cold atoms that are trapped in optical billiards
.
The driving induces diffusion in energy
,
and consequently the absorption coefficient is determined by the Kubo formula
.
External links
- Regular and Chaotic Dynamics: A widely acknowledged scientific book that treats FUM, written by A. J. Lichtenberg and M. A. Lieberman (Appl. Math. Sci. vol 38) (New York: Springer).