
Different ideal
Encyclopedia
In algebraic number theory
, the different ideal (sometimes simply the different) is defined to account for the (possible) lack of duality in the ring of integers
of an algebraic number field
K, with respect to the field trace
. It was introduced by Richard Dedekind
in 1882.
If OK is the ring of integers of K, and tr denotes the field trace from K to the rational number field Q, then
is an integral quadratic form on OK. Its discriminant
as quadratic form need not be +1 (in fact this happens only for the case K = Q). Defining a fractional ideal
I of K as the set of x ∈ K such that tr(xy) is an integer for all y in OK, then I contains OK. By definition, the different ideal δK is I−1, an ideal of OK.
The ideal norm of δK is the ideal of Z generated by the discriminant DK of K.
The different is also defined for an extension of local field
s. It plays a basic role in Pontryagin duality
for p-adic fields.
The relative different equals the annihilator of the relative differential module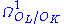 .
.
is the factorisation of p into prime ideals of L then Pi divides the relative different δL/K if and only if Pi is ramified, that is, if and only if the ramification index e(i) is greater than 1. The precise exponent to which a ramified prime P divides δ is termed the differential exponent of P and is equal to e-1 if P is tamely ramified: that is, when P does not divide e. In the case when P is wildly ramified the differential exponent lies in the range e to e+νP(e)-1 and can be computed from the orders of the higher ramification groups for Galois extensions:
, generated by a primitive element α which also generates a power integral basis. If f is the minimal polynomial for α then the different is generated by f(α).
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, the different ideal (sometimes simply the different) is defined to account for the (possible) lack of duality in the ring of integers
Ring of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
of an algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
K, with respect to the field trace
Field trace
In mathematics, the field trace is a function defined with respect to a finite field extension L/K. It is a K-linear map from L to K...
. It was introduced by Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
in 1882.
If OK is the ring of integers of K, and tr denotes the field trace from K to the rational number field Q, then
- tr(xy)
is an integral quadratic form on OK. Its discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
as quadratic form need not be +1 (in fact this happens only for the case K = Q). Defining a fractional ideal
Fractional ideal
In mathematics, in particular commutative algebra, the concept of fractional ideal is introduced in the context of integral domains and is particularly fruitful in the study of Dedekind domains. In some sense, fractional ideals of an integral domain are like ideals where denominators are allowed...
I of K as the set of x ∈ K such that tr(xy) is an integer for all y in OK, then I contains OK. By definition, the different ideal δK is I−1, an ideal of OK.
The ideal norm of δK is the ideal of Z generated by the discriminant DK of K.
The different is also defined for an extension of local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
s. It plays a basic role in Pontryagin duality
Pontryagin duality
In mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle or finite cyclic groups.-Introduction:...
for p-adic fields.
Relative different
The relative different δL/K is defined in a similar manner for an extension of number fields L/K. The relative norm of the relative different is then equal to the relative discriminant ΔL/K. In a tower of fields L/K/F the relative differents are related by δL/F = δL/K δK/F.The relative different equals the annihilator of the relative differential module
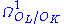 .
.Ramification
The relative different encodes the ramification data of the field extension L/K. A prime ideal p of K ramifies in L if and only if it divides the relative discriminant ΔL/K. If- p = P1e(1) ... Pke(k)
is the factorisation of p into prime ideals of L then Pi divides the relative different δL/K if and only if Pi is ramified, that is, if and only if the ramification index e(i) is greater than 1. The precise exponent to which a ramified prime P divides δ is termed the differential exponent of P and is equal to e-1 if P is tamely ramified: that is, when P does not divide e. In the case when P is wildly ramified the differential exponent lies in the range e to e+νP(e)-1 and can be computed from the orders of the higher ramification groups for Galois extensions:
-
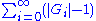 .
.
Local computation
The different may be defined for an extension of local fields L/K. In this case we may take the extension to be simpleSimple extension
In mathematics, more specifically in field theory, a simple extension is a field extension which is generated by the adjunction of a single element...
, generated by a primitive element α which also generates a power integral basis. If f is the minimal polynomial for α then the different is generated by f(α).

