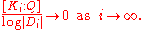Brauer-Siegel theorem
Encyclopedia
In mathematics
, the Brauer–Siegel theorem, named after Richard Brauer
and Carl Ludwig Siegel
, is an asymptotic result on the behaviour of algebraic number field
s, obtained by Richard Brauer
and Carl Ludwig Siegel
. It attempts to generalise the results known on the class numbers of imaginary quadratic fields, to a more general sequence of number fields
In all cases other than the rational field Q and imaginary quadratic fields, the regulator Ri of Ki must be taken into account, because Ki then has units of infinite order by Dirichlet's unit theorem
. The quantitative hypothesis of the standard Brauer–Siegel theorem is that if Di is the discriminant
of Ki, then
Assuming that, and the algebraic hypothesis that Ki is a Galois extension
of Q, the conclusion is that
where hi is the class number of Ki.
This result is ineffective
, as indeed was the result on quadratic fields on which it built. Effective results in the same direction were initiated in work of Harold Stark
from the early 1970s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Brauer–Siegel theorem, named after Richard Brauer
Richard Brauer
Richard Dagobert Brauer was a leading German and American mathematician. He worked mainly in abstract algebra, but made important contributions to number theory...
and Carl Ludwig Siegel
Carl Ludwig Siegel
Carl Ludwig Siegel was a mathematician specialising in number theory and celestial mechanics. He was one of the most important mathematicians of the 20th century.-Biography:...
, is an asymptotic result on the behaviour of algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
s, obtained by Richard Brauer
Richard Brauer
Richard Dagobert Brauer was a leading German and American mathematician. He worked mainly in abstract algebra, but made important contributions to number theory...
and Carl Ludwig Siegel
Carl Ludwig Siegel
Carl Ludwig Siegel was a mathematician specialising in number theory and celestial mechanics. He was one of the most important mathematicians of the 20th century.-Biography:...
. It attempts to generalise the results known on the class numbers of imaginary quadratic fields, to a more general sequence of number fields
In all cases other than the rational field Q and imaginary quadratic fields, the regulator Ri of Ki must be taken into account, because Ki then has units of infinite order by Dirichlet's unit theorem
Dirichlet's unit theorem
In mathematics, Dirichlet's unit theorem is a basic result in algebraic number theory due to Gustav Lejeune Dirichlet. It determines the rank of the group of units in the ring OK of algebraic integers of a number field K...
. The quantitative hypothesis of the standard Brauer–Siegel theorem is that if Di is the discriminant
Discriminant of an algebraic number field
In mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the algebraic number field...
of Ki, then
Assuming that, and the algebraic hypothesis that Ki is a Galois extension
Galois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
of Q, the conclusion is that
where hi is the class number of Ki.
This result is ineffective
Effective results in number theory
For historical reasons and in order to have application to the solution of Diophantine equations, results in number theory have been scrutinised more than in other branches of mathematics to see if their content is effectively computable...
, as indeed was the result on quadratic fields on which it built. Effective results in the same direction were initiated in work of Harold Stark
Harold Stark
Harold Mead Stark is an American mathematician, specializing in number theory. He is best known for his solution of the Gauss class number 1 problem, in effect correcting and completing the earlier work of Kurt Heegner; and for Stark's conjecture. He has recently collaborated with Audrey Terras on...
from the early 1970s.