Adjunction (field theory)
Encyclopedia
In abstract algebra
, adjunction is a construction in field theory
, where for a given field extension
E/F, subextensions between E and F are constructed.
F. Given a set of elements A in the larger field E we denote by F(A) the smallest subextension which contains the elements of A. We say F(A) is constructed by adjunction of the elements A to F or generated by A.
If A is finite we say F(A) is finitely generated and if A consists of a single element we say F(A) is a simple extension
. The primitive element theorem
states a finite separable extension is simple.
In a sense, a finitely generated extension is a transcendental generalization of a finite extension since, if the generators in A are all algebraic, then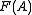
is a finite extension of F. Because of this, most examples come from algebraic geometry
.
A subextension of a finitely generated field extension is also a finitely generated extension.
be the family of all finite subsets of A. Then
.
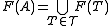In other words the adjunction of any set can be reduced to a union of adjunctions of finite sets.
Given a field extension E/F and two subset N,M of E then K(M ∪ N) = K(M)(N) = K(N)(M). This shows that any adjunction of a finite set can be reduced to a successive adjunction of single elements.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, adjunction is a construction in field theory
Field theory (mathematics)
Field theory is a branch of mathematics which studies the properties of fields. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined....
, where for a given field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
E/F, subextensions between E and F are constructed.
Definition
Let E be a field extension of a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F. Given a set of elements A in the larger field E we denote by F(A) the smallest subextension which contains the elements of A. We say F(A) is constructed by adjunction of the elements A to F or generated by A.
If A is finite we say F(A) is finitely generated and if A consists of a single element we say F(A) is a simple extension
Simple extension
In mathematics, more specifically in field theory, a simple extension is a field extension which is generated by the adjunction of a single element...
. The primitive element theorem
Primitive element theorem
In mathematics, more specifically in the area of modern algebra known as field theory, the primitive element theorem or Artin's theorem on primitive elements is a result characterizing the finite degree field extensions that possess a primitive element...
states a finite separable extension is simple.
In a sense, a finitely generated extension is a transcendental generalization of a finite extension since, if the generators in A are all algebraic, then
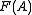is a finite extension of F. Because of this, most examples come from algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
.
A subextension of a finitely generated field extension is also a finitely generated extension.
Examples
- Given a field extension E/F then F(Ø) = F and F(E) = E.
- The complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s are constructed by adjunction of the imaginary unitImaginary unitIn mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
to the real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, that is C=R(i).
Properties
Given a field extension E/F and a subset A of E, let be the family of all finite subsets of A. Then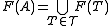.In other words the adjunction of any set can be reduced to a union of adjunctions of finite sets.
Given a field extension E/F and two subset N,M of E then K(M ∪ N) = K(M)(N) = K(N)(M). This shows that any adjunction of a finite set can be reduced to a successive adjunction of single elements.