Direct image functor
Encyclopedia
In mathematics
, in the field of sheaf theory and especially in algebraic geometry
, the direct image functor generalizes the notion of a section of a sheaf to the relative case.
s, and Sh(–) the category
of sheaves of abelian group
s on a topological space. The direct image functor
sends a sheaf F on X to its direct image presheaf
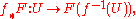
which turns out be a sheaf on Y. This assignment is functorial, i.e. a morphism of sheaves φ: F → G on X gives rise to a morphism of sheaves f∗(φ): f∗(F) → f∗(G) on Y.
Let f: X → Y be a continuous map of topological spaces or a morphism of schemes. Then the exceptional inverse image is a functor
Rf!: D(Y) → D(X).
, such as etale sheaves
. Instead of the above preimage f−1(U) the fiber product of U and X over Y is used.
s of the direct image. They are called higher direct images and denoted Rq f∗.
One can show that there is a similar expression as above for higher direct images: for a sheaf F on X, Rq f∗(F) is the sheaf associated to the presheaves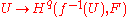
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the field of sheaf theory and especially in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the direct image functor generalizes the notion of a section of a sheaf to the relative case.
Definition
Let f: X → Y be a continuous mapping of topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s, and Sh(–) the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of sheaves of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s on a topological space. The direct image functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
sends a sheaf F on X to its direct image presheaf
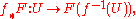
which turns out be a sheaf on Y. This assignment is functorial, i.e. a morphism of sheaves φ: F → G on X gives rise to a morphism of sheaves f∗(φ): f∗(F) → f∗(G) on Y.
Example
If Y is a point, then the direct image equals the global sections functor.Let f: X → Y be a continuous map of topological spaces or a morphism of schemes. Then the exceptional inverse image is a functor
Rf!: D(Y) → D(X).
Variants
A similar definition applies to sheaves on topoiTopos
In mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
, such as etale sheaves
Étale
In mathematics, more specifically in algebra, the adjective étale refers to several closely related concepts:* Étale morphism** Formally étale morphism* Étale cohomology* Étale topology* Étale fundamental group* Étale space* Étale group scheme...
. Instead of the above preimage f−1(U) the fiber product of U and X over Y is used.
Higher direct images
The direct image functor is left exact, but usually not right exact. Hence one can consider the right derived functorDerived functor
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
s of the direct image. They are called higher direct images and denoted Rq f∗.
One can show that there is a similar expression as above for higher direct images: for a sheaf F on X, Rq f∗(F) is the sheaf associated to the presheaves
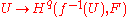
Properties
- The direct image functor is right adjoint to the inverse image functorInverse image functorIn mathematics, the inverse image functor is a contravariant construction of sheaves. The direct image functor is the primary operation on sheaves, with the simplest definition. The inverse image exhibits some relatively subtle features.-Definition:...
, which means that for any continuous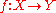
and sheaves 
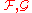respectively on X, Y, there is a natural isomorphism:
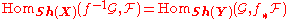. - If f is the inclusion of a closed subspace X ⊂ Y then f∗ is exact. Actually, in this case f∗ is an equivalenceEquivalence of categoriesIn category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
between sheaves on X and sheaves on Y supported on X.