
Kan extension
Encyclopedia
Kan extensions are universal constructs
in category theory
, a branch of mathematics
. They are closely related to adjoints
, but are also related to limits
and ends. They are named after Daniel M. Kan
, who constructed certain (Kan) extensions using limits
in 1960.
An early use of (what is now known as) a Kan extension from 1956 was in homological algebra
to compute derived functor
s.
In Categories for the Working Mathematician
Saunders Mac Lane
titled a section "All Concepts Are Kan Extensions", and went on to write that
The definition, not surprisingly, is at a high level of abstraction. When specialised to posets, it becomes a relatively familiar type of question on 'constrained optimization'.
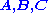
and two functor
s
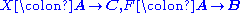 ,
,
and comes in two varieties: the "left" Kan extension and the "right" Kan extension of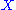 along
along  .
.
Formally, the right Kan extension of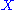 along
along 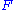 consists of a functor
consists of a functor  and a natural transformation
and a natural transformation 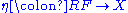 which is universal with respect to the specification, in the sense that for any functor
which is universal with respect to the specification, in the sense that for any functor 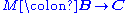 and natural transformation
and natural transformation 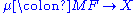 , a unique natural transformation
, a unique natural transformation  is defined and fits into a commutative diagram
is defined and fits into a commutative diagram
The functor R is often written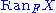 .
.
As with the other universal constructs
in category theory
, the "left" version of the Kan extension is dual
to the "right" one and is obtained by replacing all categories by their opposite
s. The effect of this on the description above is merely to reverse the direction of the natural transformations (recall that a natural transformation
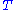 between the functors
between the functors  consists of the data of an arrow
consists of the data of an arrow 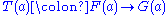 for every object
for every object  of
of  , satisfying a "naturality" property. When we pass to the opposite categories, the source and target of
, satisfying a "naturality" property. When we pass to the opposite categories, the source and target of  are swapped, causing
are swapped, causing 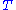 to act in the opposite direction).
to act in the opposite direction).
This gives rise to the alternate description: the left Kan extension of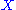 along
along 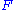 consists of a functor
consists of a functor 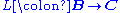 and a natural transformation
and a natural transformation  which are universal with respect to this specification, in the sense that for any other functor
which are universal with respect to this specification, in the sense that for any other functor 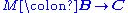 and natural transformation
and natural transformation 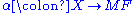 , a unique natural transformation
, a unique natural transformation 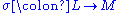 exists and fits into a commutative diagram:
exists and fits into a commutative diagram:
The functor L is often written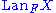 .
.
The use of the word "the" (as in "the left Kan extension") is justified by the fact that, as with all universal constructions, if the object defined exists, then it is unique up to unique isomorphism. In this case, that means that (for left Kan extensions) if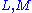 are two left Kan extensions of
are two left Kan extensions of 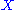 along
along  , and
, and 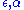 are the corresponding transformations, then there exists a unique isomorphism of functors
are the corresponding transformations, then there exists a unique isomorphism of functors 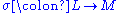 such that the first diagram above commutes. Likewise for right Kan extensions.
such that the first diagram above commutes. Likewise for right Kan extensions.
Kan extensions as (co)limits
Suppose that 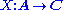 and
and 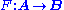 are two functors. If A is small and C is cocomplete, then there exists a left Kan extension
are two functors. If A is small and C is cocomplete, then there exists a left Kan extension 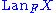 of
of 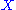 along
along 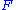 , defined at each object b of B by
, defined at each object b of B by

where the colimit is taken over the comma category
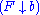 .
.
Dually, if A is small and C is complete, then right Kan extensions along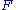 exist, and can be computed as limits.
exist, and can be computed as limits.
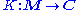 and
and 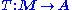
are two functors such that for all objects m and m of M and all objects c of C, the copowers exist in A. Then the functor T has a left Kan extension L along K, which is such that, for every object c of C,
exist in A. Then the functor T has a left Kan extension L along K, which is such that, for every object c of C,
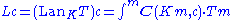
when the above coend exists for every object c of C.
Dually, right Kan extensions can be computed by the formula
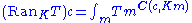 .
.
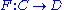 can be expressed as a Kan extension by
can be expressed as a Kan extension by
where is the unique functor from
is the unique functor from  to [0] (the category with one object and one arrow). The colimit of
to [0] (the category with one object and one arrow). The colimit of  can be expressed similarly by
can be expressed similarly by
 .
.
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
in category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
. They are closely related to adjoints
Adjoint functors
In mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
, but are also related to limits
Limit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
and ends. They are named after Daniel M. Kan
Daniel Kan
Daniel Marinus Kan is a mathematician working in homotopy theory. He has been a prolific contributor to the field for the last five decades, having authored or coauthored several dozen research papers and monographs. The general theme of his career has been abstract homotopy theory.He is an...
, who constructed certain (Kan) extensions using limits
Limit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
in 1960.
An early use of (what is now known as) a Kan extension from 1956 was in homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
to compute derived functor
Derived functor
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
s.
In Categories for the Working Mathematician
Categories for the Working Mathematician
Categories for the Working Mathematician is a textbook in category theory written by American mathematician Saunders Mac Lane, who cofounded the subject together with Samuel Eilenberg. It was first published in 1971, and is based on his lectures on the subject given at the University of Chicago,...
Saunders Mac Lane
Saunders Mac Lane
Saunders Mac Lane was an American mathematician who cofounded category theory with Samuel Eilenberg.-Career:...
titled a section "All Concepts Are Kan Extensions", and went on to write that
- The notion of Kan extensions subsumes all the other fundamental concepts of category theory.
The definition, not surprisingly, is at a high level of abstraction. When specialised to posets, it becomes a relatively familiar type of question on 'constrained optimization'.
Definition
A Kan extension proceeds from the data of three categories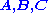
and two functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s
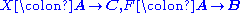 ,
,and comes in two varieties: the "left" Kan extension and the "right" Kan extension of
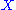 along
along  .
.Formally, the right Kan extension of
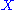 along
along 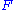 consists of a functor
consists of a functor  and a natural transformation
and a natural transformation 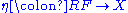 which is universal with respect to the specification, in the sense that for any functor
which is universal with respect to the specification, in the sense that for any functor 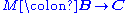 and natural transformation
and natural transformation 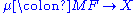 , a unique natural transformation
, a unique natural transformation  is defined and fits into a commutative diagram
is defined and fits into a commutative diagram- (where
 is the natural transformation with
is the natural transformation with 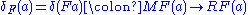 for any object
for any object  of
of 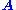 ).
).
The functor R is often written
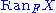 .
.As with the other universal constructs
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
in category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, the "left" version of the Kan extension is dual
Dual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
to the "right" one and is obtained by replacing all categories by their opposite
Opposite category
In category theory, a branch of mathematics, the opposite category or dual category Cop of a given category C is formed by reversing the morphisms, i.e. interchanging the source and target of each morphism. Doing the reversal twice yields the original category, so the opposite of an opposite...
s. The effect of this on the description above is merely to reverse the direction of the natural transformations (recall that a natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
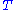 between the functors
between the functors  consists of the data of an arrow
consists of the data of an arrow 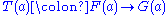 for every object
for every object  of
of  , satisfying a "naturality" property. When we pass to the opposite categories, the source and target of
, satisfying a "naturality" property. When we pass to the opposite categories, the source and target of  are swapped, causing
are swapped, causing 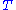 to act in the opposite direction).
to act in the opposite direction).This gives rise to the alternate description: the left Kan extension of
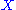 along
along 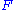 consists of a functor
consists of a functor 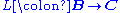 and a natural transformation
and a natural transformation  which are universal with respect to this specification, in the sense that for any other functor
which are universal with respect to this specification, in the sense that for any other functor 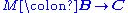 and natural transformation
and natural transformation 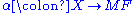 , a unique natural transformation
, a unique natural transformation 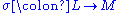 exists and fits into a commutative diagram:
exists and fits into a commutative diagram:- (where
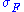 is the natural transformation with
is the natural transformation with  for any object
for any object  of
of 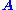 ).
).
The functor L is often written
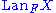 .
.The use of the word "the" (as in "the left Kan extension") is justified by the fact that, as with all universal constructions, if the object defined exists, then it is unique up to unique isomorphism. In this case, that means that (for left Kan extensions) if
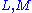 are two left Kan extensions of
are two left Kan extensions of 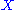 along
along  , and
, and 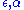 are the corresponding transformations, then there exists a unique isomorphism of functors
are the corresponding transformations, then there exists a unique isomorphism of functors 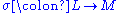 such that the first diagram above commutes. Likewise for right Kan extensions.
such that the first diagram above commutes. Likewise for right Kan extensions.Kan extensions as (co)limitsLimit (category theory)In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
Suppose that 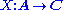 and
and 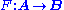 are two functors. If A is small and C is cocomplete, then there exists a left Kan extension
are two functors. If A is small and C is cocomplete, then there exists a left Kan extension 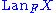 of
of 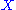 along
along 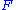 , defined at each object b of B by
, defined at each object b of B by
where the colimit is taken over the comma category
Comma category
In mathematics, a comma category is a construction in category theory. It provides another way of looking at morphisms: instead of simply relating objects of a category to one another, morphisms become objects in their own right. This notion was introduced in 1963 by F. W...
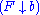 .
.Dually, if A is small and C is complete, then right Kan extensions along
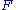 exist, and can be computed as limits.
exist, and can be computed as limits.Kan extensions as coends
Suppose that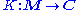 and
and 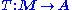
are two functors such that for all objects m and m of M and all objects c of C, the copowers
 exist in A. Then the functor T has a left Kan extension L along K, which is such that, for every object c of C,
exist in A. Then the functor T has a left Kan extension L along K, which is such that, for every object c of C,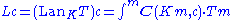
when the above coend exists for every object c of C.
Dually, right Kan extensions can be computed by the formula
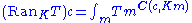 .
.Limits as Kan extensions
The limit of a functor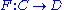 can be expressed as a Kan extension by
can be expressed as a Kan extension by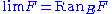
where
 is the unique functor from
is the unique functor from  to [0] (the category with one object and one arrow). The colimit of
to [0] (the category with one object and one arrow). The colimit of  can be expressed similarly by
can be expressed similarly by .
.

