D-module
Encyclopedia
In mathematics
, a D-module is a module
over a ring
D of differential operator
s. The major interest of such D-modules is as an approach to the theory of linear partial differential equations. Since around 1970, D-module theory has been built up, mainly as a response to the ideas of Mikio Sato
on algebraic analysis
, and expanding on the work of Sato and Joseph Bernstein
on the Bernstein–Sato polynomial
.
Early major results were the Kashiwara constructibility theorem and Kashiwara index theorem of Masaki Kashiwara
. The methods of D-module theory have always been drawn from sheaf theory and other techniques with inspiration from the work of Alexander Grothendieck
in algebraic geometry
. The approach is global in character, and differs from the functional analysis
techniques traditionally used to study differential operators. The strongest results are obtained for over-determined systems (holonomic systems), and on the characteristic variety cut out by the symbols
, in the good case for which it is a Lagrangian submanifold of the cotangent bundle
of maximal dimension (involutive systems). The techniques were taken up from the side of the Grothendieck school by Zoghman Mebkhout
, who obtained a general, derived category
version of the Riemann–Hilbert correspondence in all dimensions.
K of characteristic
zero. It is the algebra consisting of polynomials in the following variables
where all of the variables xi and ∂j commute with each other, but the commutator
For any polynomial f(x1, ..., xn), this implies the relation
thereby relating the Weyl algebra to differential equations.
An (algebraic) D-module is, by definition, a left module over the ring An(K). Examples for D-modules include the Weyl algebra itself (acting on itself by left multiplication), the (commutative) polynomial ring
K[x1, ..., xn], where xi acts by multiplication and ∂j acts by partial differentiation with respect to xj and, in a similar vein, the ring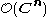
of holomorphic functions on Cn, the complex plane.
Given some differential operator
P = an(x) ∂n + ... + a1(x) ∂1 + a0(x), where x is a complex variable, ai(x) are polynomials, the quotient module M = A1(C)/A1(C)P is closely linked to space of solutions of the differential equation
where f is some holomorphic function in C, say. The vector space consisting of the solutions of that equation is given by the space of homomorphisms of D-modules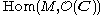
.
X defined over an algebraically closed field K of characteristic zero, such as K = C. The sheaf
of differential operators DX is defined to be the OX-module generated by the vector field
s on X, interpreted as derivations
. A (left) DX-module M is an OX-module with a left action
of DX. Giving such an action is equivalent to specifying a K-linear map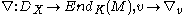
satisfying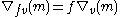
(Leibniz rule)
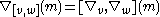
Here f is a regular function on X, v and w are vector fields, m a local section of M, [−, −] denotes the commutator
. Therefore, if M is in addition a locally free OX-module, giving M a D-module structure is nothing else than equipping the vector bundle
associated to M with a flat (or integrable) connection
.
As the ring DX is noncommutative, left and right D-modules have to be distinguished. However, the two notions can be exchanged, since there is an equivalence of categories
between both types of modules, given by mapping a left module M to the tensor product
M ⊗ ΩX, where ΩX is the line bundle
given by the highest exterior power of differential 1-forms
on X. This bundle has a natural right action determined by
where v is a differential operator of order one, that is to say a vector field, ω a n-form (n = dim X), and Lie denotes the Lie derivative
.
Locally, after choosing some system of coordinates x1, ..., xn (n = dim X) on X, which determine a basis ∂1, ..., ∂n of the tangent space
of X, sections of DX can be uniquely represented as expressions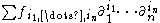
, where the 
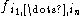are regular function
s on X.
In particular, when X is the n-dimensional affine space
, this DX is the Weyl algebra in n variables.
Many basic properties of D-modules are local and parallel the situation of coherent sheaves
. This builds on the fact that DX is a locally free sheaf of OX-modules, albeit of infinite rank, as the above-mentioned OX-basis shows. A DX-module that is coherent as an OX-module can be shown to be necessarily locally free (of finite rank).
comparable to the ones for coherent sheaves. For a map f: X → Y of smooth varieties, the definitions are this:
This is equipped with a left DX action in a way that emulates the chain rule
, and with the natural right action of f−1(DX). The pullback is defined as
Here M is a left DY-module, while its pullback is a left module over X. This functor is right exact, its left derived functor
is denoted Lf∗. Conversely, for a right DX-module N,
is a right DY-module. Since this mixes the right exact tensor product with the left exact pushforward, it is common to set instead
Because of this, much of the theory of D-modules is developed using the full power of homological algebra
, in particular derived categories
.
. Moreover, it is simple
, that is to say, its only left and right ideal are the zero ideal and the whole ring. These properties make the study of D-modules manageable. Notably, standard notions from commutative algebra
such as Hilbert polynomial
, multiplicity and length
of modules carry over to D-modules. More precisely, DX is equipped with the Bernstein filtration, that is, the filtration such that FpAn(K) consists of K-linear combinations of differential operators xα∂β with |α|+|β| ≤ p (using multiindex notation). The associated graded ring is seen to be isomorphic to the polynomial ring in 2n indeterminates. In particular it is commutative.
Finitely generated D-modules M are endowed with so-called "good" filtrations F∗M, which are ones compatible with F∗An(K), essentially parallel to the situation of the Artin-Rees lemma
. The Hilbert polynomial is defined to be the numerical polynomial
that agrees with the function
for large n. The dimension d(M) of a An(K)-module M is defined to be the degree of the Hilbert polynomial. It is bounded by the Bernstein inequality
A module whose dimension attains the least possible value, n, is called holonomic.
The A1(K)-module M = A1(K)/A1(K)P (see above) is holonomic for any nonzero differential operator P, but a similar claim for higher-dimensional Weyl algebras does not hold.
T∗X.
The characteristic variety is defined to be the subvariety of the cotangent bundle
cut out by the radical
of the annihilator
of gr M, where again M is equipped with a suitable filtration (with respect to the order filtration on DX). As usual, the affine construction then glues to arbitrary varieties.
The Bernstein inequality continues to hold for any (smooth) variety X. While the upper bound is an immediate consequence of the above interpretation of in terms of the cotangent bundle, the lower bound is more subtle.
For any D-module M, the dual module is defined by
Holonomic modules can also be characterized by a homological
condition: M is holonomic if and only if D(M) is concentrated (seen as an object in the derived category of D-modules) in degree 0. This fact is a first glimpse of Verdier duality
and the Riemann–Hilbert correspondence
. It is proven by extending the homological study of regular ring
s (especially what is related to global homological dimension) to the filtered ring DX.
Another characterization of holonomic modules is via symplectic geometry. The characteristic variety Ch(M) of any D-module M is, seen as a subvariety of the cotangent bundle T∗X of X, an involutive variety. The module is holonomic if and only if Ch(M) is Lagrangian.
.
establishes a link between certain D-modules and constructible sheaves. As such, it provided a motivation for introducing perverse sheaves
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a D-module is a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
D of differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s. The major interest of such D-modules is as an approach to the theory of linear partial differential equations. Since around 1970, D-module theory has been built up, mainly as a response to the ideas of Mikio Sato
Mikio Sato
is a Japanese mathematician, who started the field of algebraic analysis. He studied at the University of Tokyo, and then did graduate study in physics as a student of Shin'ichiro Tomonaga...
on algebraic analysis
Algebraic analysis
Algebraic analysis is an area of mathematics that deals with systems of linear partial differential equations by using sheaf theory and complex analysis to study properties and generalizations of functions such as hyperfunctions and microfunctions.-See also:...
, and expanding on the work of Sato and Joseph Bernstein
Joseph Bernstein
Joseph Bernstein is an Israeli mathematician working at Tel Aviv University. He works in algebraic geometry, representation theory, and number theory....
on the Bernstein–Sato polynomial
Bernstein–Sato polynomial
In mathematics, the Bernstein–Sato polynomial is a polynomial related to differential operators, introduced independently by and , . It is also known as the b-function, the b-polynomial, and the Bernstein polynomial, though it is not related to the Bernstein polynomials used in approximation...
.
Early major results were the Kashiwara constructibility theorem and Kashiwara index theorem of Masaki Kashiwara
Masaki Kashiwara
is a Japanese mathematician. He was a student of Mikio Sato at the University of Tokyo. Sato and Kashiwara have collaborated on algebraic analysis and D-module theory.He is a member of the French Academy of Sciences.- Concepts named after Kashiwara :...
. The methods of D-module theory have always been drawn from sheaf theory and other techniques with inspiration from the work of Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. The approach is global in character, and differs from the functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
techniques traditionally used to study differential operators. The strongest results are obtained for over-determined systems (holonomic systems), and on the characteristic variety cut out by the symbols
Symbol of a differential operator
In mathematics, the symbol of a linear differential operator associates to a differential operator a polynomial by, roughly speaking, replacing each partial derivative by a new variable. The symbol of a differential operator has broad applications to Fourier analysis. In particular, in this...
, in the good case for which it is a Lagrangian submanifold of the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
of maximal dimension (involutive systems). The techniques were taken up from the side of the Grothendieck school by Zoghman Mebkhout
Zoghman Mebkhout
Zoghman Mebkhout is an Algerian mathematician known for his work in algebraic analysis, geometry, and representation theory, more precisely on the theory of D-modules ....
, who obtained a general, derived category
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
version of the Riemann–Hilbert correspondence in all dimensions.
Introduction: modules over the Weyl algebra
The first case of algebraic D-modules are modules over the Weyl algebra An(K) over a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K of characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
zero. It is the algebra consisting of polynomials in the following variables
- x1, ..., xn, ∂1, ..., ∂n.
where all of the variables xi and ∂j commute with each other, but the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
- [∂i, xi] = ∂ixi − xi∂i = 1.
For any polynomial f(x1, ..., xn), this implies the relation
- [∂i, f] = ∂f / ∂xi,
thereby relating the Weyl algebra to differential equations.
An (algebraic) D-module is, by definition, a left module over the ring An(K). Examples for D-modules include the Weyl algebra itself (acting on itself by left multiplication), the (commutative) polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
K[x1, ..., xn], where xi acts by multiplication and ∂j acts by partial differentiation with respect to xj and, in a similar vein, the ring
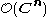of holomorphic functions on Cn, the complex plane.Given some differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
P = an(x) ∂n + ... + a1(x) ∂1 + a0(x), where x is a complex variable, ai(x) are polynomials, the quotient module M = A1(C)/A1(C)P is closely linked to space of solutions of the differential equation
- P f = 0,
where f is some holomorphic function in C, say. The vector space consisting of the solutions of that equation is given by the space of homomorphisms of D-modules
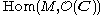.D-modules on algebraic varieties
The general theory of D-modules is developed on a smooth algebraic varietyAlgebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
X defined over an algebraically closed field K of characteristic zero, such as K = C. The sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of differential operators DX is defined to be the OX-module generated by the vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s on X, interpreted as derivations
Differential algebra
In mathematics, differential rings, differential fields, and differential algebras are rings, fields, and algebras equipped with a derivation, which is a unary function that is linear and satisfies the Leibniz product law...
. A (left) DX-module M is an OX-module with a left action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of DX. Giving such an action is equivalent to specifying a K-linear map
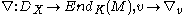
satisfying
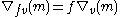
(Leibniz rule)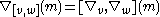Here f is a regular function on X, v and w are vector fields, m a local section of M, [−, −] denotes the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
. Therefore, if M is in addition a locally free OX-module, giving M a D-module structure is nothing else than equipping the vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
associated to M with a flat (or integrable) connection
Connection (vector bundle)
In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...
.
As the ring DX is noncommutative, left and right D-modules have to be distinguished. However, the two notions can be exchanged, since there is an equivalence of categories
Equivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
between both types of modules, given by mapping a left module M to the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
M ⊗ ΩX, where ΩX is the line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
given by the highest exterior power of differential 1-forms
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
on X. This bundle has a natural right action determined by
- ω ⋅ v := − Liev (ω),
where v is a differential operator of order one, that is to say a vector field, ω a n-form (n = dim X), and Lie denotes the Lie derivative
Lie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
.
Locally, after choosing some system of coordinates x1, ..., xn (n = dim X) on X, which determine a basis ∂1, ..., ∂n of the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
of X, sections of DX can be uniquely represented as expressions
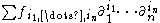, where the 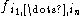are regular functionRegular function
In mathematics, a regular function is a function that is analytic and single-valued in a given region. In complex analysis, any complex regular function is known as a holomorphic function...
s on X.
In particular, when X is the n-dimensional affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
, this DX is the Weyl algebra in n variables.
Many basic properties of D-modules are local and parallel the situation of coherent sheaves
Coherent sheaf
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a specific class of sheaves having particularly manageable properties closely linked to the geometrical properties of the underlying space. The definition of coherent sheaves is made with...
. This builds on the fact that DX is a locally free sheaf of OX-modules, albeit of infinite rank, as the above-mentioned OX-basis shows. A DX-module that is coherent as an OX-module can be shown to be necessarily locally free (of finite rank).
Functoriality
D-modules on different algebraic varieties are connected by pullback and pushforward functorsImage functors for sheaves
In mathematics, especially in sheaf theory, a domain applied in areas such as topology, logic and algebraic geometry, there are four image functors for sheaves which belong together in various senses....
comparable to the ones for coherent sheaves. For a map f: X → Y of smooth varieties, the definitions are this:
- DX→Y := OX ⊗f−1(OX) f−1(DX)
This is equipped with a left DX action in a way that emulates the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
, and with the natural right action of f−1(DX). The pullback is defined as
- f∗(M) := DX→Y ⊗f−1(DX) f−1(M).
Here M is a left DY-module, while its pullback is a left module over X. This functor is right exact, its left derived functor
Derived functor
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
is denoted Lf∗. Conversely, for a right DX-module N,
- f∗(N) := f∗(N ⊗DX DX→Y)
is a right DY-module. Since this mixes the right exact tensor product with the left exact pushforward, it is common to set instead
- f∗(N) := Rf∗(N ⊗LDX DX→Y).
Because of this, much of the theory of D-modules is developed using the full power of homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, in particular derived categories
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
.
Holonomic modules over the Weyl algebra
It can be shown that the Weyl algebra is a (left and right) Noetherian ringNoetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
. Moreover, it is simple
Simple ring
In abstract algebra, a simple ring is a non-zero ring that has no ideal besides the zero ideal and itself. A simple ring can always be considered as a simple algebra. This notion must not be confused with the related one of a ring being simple as a left module over itself...
, that is to say, its only left and right ideal are the zero ideal and the whole ring. These properties make the study of D-modules manageable. Notably, standard notions from commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
such as Hilbert polynomial
Hilbert polynomial
In commutative algebra, the Hilbert polynomial of a graded commutative algebra or graded module is a polynomial in one variable that measures the rate of growth of the dimensions of its homogeneous components...
, multiplicity and length
Length of a module
In abstract algebra, the length of a module is a measure of the module's "size". It is defined to be the length of the longest chain of submodules and is a generalization of the concept of dimension for vector spaces...
of modules carry over to D-modules. More precisely, DX is equipped with the Bernstein filtration, that is, the filtration such that FpAn(K) consists of K-linear combinations of differential operators xα∂β with |α|+|β| ≤ p (using multiindex notation). The associated graded ring is seen to be isomorphic to the polynomial ring in 2n indeterminates. In particular it is commutative.
Finitely generated D-modules M are endowed with so-called "good" filtrations F∗M, which are ones compatible with F∗An(K), essentially parallel to the situation of the Artin-Rees lemma
Artin-Rees lemma
In mathematics, the Artin–Rees lemma is a result in the theory of rings and modules. It was proved in the 1950s in independent works by the mathematicians Emil Artin and David Rees; a special case was known to Oscar Zariski prior to their work...
. The Hilbert polynomial is defined to be the numerical polynomial
Numerical polynomial
In mathematics, a numerical polynomial is a polynomial with rational coefficients that takes integer values on integers. They are also called integer-valued polynomials....
that agrees with the function
- n ↦ dimK FnM
for large n. The dimension d(M) of a An(K)-module M is defined to be the degree of the Hilbert polynomial. It is bounded by the Bernstein inequality
- n ≤ d(M) ≤ 2n.
A module whose dimension attains the least possible value, n, is called holonomic.
The A1(K)-module M = A1(K)/A1(K)P (see above) is holonomic for any nonzero differential operator P, but a similar claim for higher-dimensional Weyl algebras does not hold.
General definition
As mentioned above, modules over the Weyl algebra correspond to D-modules on affine space. The Bernstein filtration not being available on DX for general varieties X, the definition is generalized to arbitrary affine smooth varieties X by means of order filtration on DX, defined by the order of differential operators. The associated graded ring gr DX is given by regular functions on the cotangent bundleCotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
T∗X.
The characteristic variety is defined to be the subvariety of the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
cut out by the radical
Radical of an ideal
In commutative ring theory, a branch of mathematics, the radical of an ideal I is an ideal such that an element x is in the radical if some power of x is in I. A radical ideal is an ideal that is its own radical...
of the annihilator
Annihilator (ring theory)
In mathematics, specifically module theory, annihilators are a concept that generalizes torsion and orthogonal complement.-Definitions:Let R be a ring, and let M be a left R-module. Choose a nonempty subset S of M...
of gr M, where again M is equipped with a suitable filtration (with respect to the order filtration on DX). As usual, the affine construction then glues to arbitrary varieties.
The Bernstein inequality continues to hold for any (smooth) variety X. While the upper bound is an immediate consequence of the above interpretation of in terms of the cotangent bundle, the lower bound is more subtle.
Properties and characterizations
Holonomic modules have a tendency to behave like finite-dimensional vector spaces. For example, their length is finite. Also, M is holonomic if and only if all cohomology groups of the complex Li∗(M) are finite-dimensional K-vector spaces, where i is the closed immersion of any point of X.For any D-module M, the dual module is defined by
Holonomic modules can also be characterized by a homological
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
condition: M is holonomic if and only if D(M) is concentrated (seen as an object in the derived category of D-modules) in degree 0. This fact is a first glimpse of Verdier duality
Verdier duality
In mathematics, Verdier duality is a generalization of the Poincaré duality of manifolds to locally compact spaces with singularities. Verdier duality was introduced by , as an analog for locally compact spaces of the coherent duality for schemes due to Grothendieck...
and the Riemann–Hilbert correspondence
Riemann–Hilbert correspondence
In mathematics, the Riemann–Hilbert correspondence is a generalization of Hilbert's twenty-first problem to higher dimensions. The original setting was for Riemann surfaces, where it was about the existence of regular differential equations with prescribed monodromy groups...
. It is proven by extending the homological study of regular ring
Regular ring
In commutative algebra, a regular ring is a commutative noetherian ring, such that the localization at every prime ideal is a regular local ring: that is, every such localization has the property that the minimal number of generators of its maximal ideal is equal to its Krull dimension.Jean-Pierre...
s (especially what is related to global homological dimension) to the filtered ring DX.
Another characterization of holonomic modules is via symplectic geometry. The characteristic variety Ch(M) of any D-module M is, seen as a subvariety of the cotangent bundle T∗X of X, an involutive variety. The module is holonomic if and only if Ch(M) is Lagrangian.
Applications
One of the early applications of holonomic D-modules was the Bernstein–Sato polynomialBernstein–Sato polynomial
In mathematics, the Bernstein–Sato polynomial is a polynomial related to differential operators, introduced independently by and , . It is also known as the b-function, the b-polynomial, and the Bernstein polynomial, though it is not related to the Bernstein polynomials used in approximation...
.
Riemann–Hilbert correspondence
The Riemann–Hilbert correspondenceRiemann–Hilbert correspondence
In mathematics, the Riemann–Hilbert correspondence is a generalization of Hilbert's twenty-first problem to higher dimensions. The original setting was for Riemann surfaces, where it was about the existence of regular differential equations with prescribed monodromy groups...
establishes a link between certain D-modules and constructible sheaves. As such, it provided a motivation for introducing perverse sheaves
Perverse sheaf
The mathematical term perverse sheaves refers to a certain abelian category associated to a topological space X, which may be a real or complex manifold, or a more general Topologically stratified space, usually singular...
.