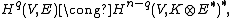Serre duality
Encyclopedia
In algebraic geometry
, a branch of mathematics
, Serre duality is a duality
present on non-singular projective algebraic varieties
V of dimension n (and in greater generality for vector bundle
s and further, for coherent sheaves
). It shows that a cohomology
group Hi is the dual space
of another one, Hn−i. If the variety is defined over the complex number
s, this yields different information from Poincaré duality
, which relates Hi to H2n−i, considering V as a real manifold of dimension 2n.
In the case for holomorphic vector bundle E over a smooth compact complex manifold V, the statement is in the form:
in which V is not necessarily projective.
s was already implicit in the Riemann-Roch theorem. For a curve C the coherent groups Hi vanish for i > 1; but H1 does enter implicitly. In fact, the basic relation of the theorem involves l(D) and l(K−D), where D is a divisor
and K is a divisor of the canonical class. After Serre
we recognise l(K−D) as the dimension of H1(D), where now D means the line bundle
determined by the divisor D. That is, Serre duality in this case relates groups H1(D) and H0(KD*), and we are reading off dimensions (notation: K is the canonical line bundle, D* is the dual line bundle, and juxtaposition is the tensor product
of line bundles).
In this formulation the Riemann-Roch theorem can be viewed as a computation of the Euler characteristic of a sheaf
in terms of the genus
of the curve, which is
and the degree of D. It is this expression that can be generalised to higher dimensions.
Serre duality of curves is therefore something very classical; but it has an interesting light to cast. For example, in Riemann surface
theory, the deformation theory
of complex structures is studied classically by means of quadratic differential
s (namely sections of L(K2)). The deformation theory
of Kunihiko Kodaira and D. C. Spencer identifies deformations via H1(T), where T is the tangent bundle
sheaf K*. The duality shows why these approaches coincide.
. In the generalisation of Alexander Grothendieck
, Serre duality becomes a part of coherent duality
in a much broader setting. While the role of K above in general Serre duality is played by the determinant line bundle of the cotangent bundle
, when V is a manifold, in full generality K cannot merely be a single sheaf in the absence of some hypothesis of non-singularity on V. The formulation in full generality uses a derived category
and Ext functor
s, to allow for the fact that K is now represented by a chain complex
of sheaves, namely, the dualizing complex. Nevertheless, the statement of the theorem is recognisably Serre's.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Serre duality is a duality
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
present on non-singular projective algebraic varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
V of dimension n (and in greater generality for vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s and further, for coherent sheaves
Coherent sheaf
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a specific class of sheaves having particularly manageable properties closely linked to the geometrical properties of the underlying space. The definition of coherent sheaves is made with...
). It shows that a cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
group Hi is the dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of another one, Hn−i. If the variety is defined over the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, this yields different information from Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
, which relates Hi to H2n−i, considering V as a real manifold of dimension 2n.
In the case for holomorphic vector bundle E over a smooth compact complex manifold V, the statement is in the form:
in which V is not necessarily projective.
Algebraic curve
The case of algebraic curveAlgebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
s was already implicit in the Riemann-Roch theorem. For a curve C the coherent groups Hi vanish for i > 1; but H1 does enter implicitly. In fact, the basic relation of the theorem involves l(D) and l(K−D), where D is a divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
and K is a divisor of the canonical class. After Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
we recognise l(K−D) as the dimension of H1(D), where now D means the line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
determined by the divisor D. That is, Serre duality in this case relates groups H1(D) and H0(KD*), and we are reading off dimensions (notation: K is the canonical line bundle, D* is the dual line bundle, and juxtaposition is the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of line bundles).
In this formulation the Riemann-Roch theorem can be viewed as a computation of the Euler characteristic of a sheaf
- h0(D) − h1(D),
in terms of the genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
of the curve, which is
- h1(C,OC),
and the degree of D. It is this expression that can be generalised to higher dimensions.
Serre duality of curves is therefore something very classical; but it has an interesting light to cast. For example, in Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
theory, the deformation theory
Deformation theory
In mathematics, deformation theory is the study of infinitesimal conditions associated with varying a solution P of a problem to slightly different solutions Pε, where ε is a small number, or vector of small quantities. The infinitesimal conditions are therefore the result of applying the approach...
of complex structures is studied classically by means of quadratic differential
Quadratic differential
In mathematics, a quadratic differential on a Riemann surface is a section of the symmetric square of the holomorphic cotangent bundle.If the section is holomorphic, then the quadratic differentialis said to be holomorphic...
s (namely sections of L(K2)). The deformation theory
Deformation theory
In mathematics, deformation theory is the study of infinitesimal conditions associated with varying a solution P of a problem to slightly different solutions Pε, where ε is a small number, or vector of small quantities. The infinitesimal conditions are therefore the result of applying the approach...
of Kunihiko Kodaira and D. C. Spencer identifies deformations via H1(T), where T is the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
sheaf K*. The duality shows why these approaches coincide.
Origin and generalisations
The origin of the theory lies in Serre's earlier work on several complex variablesSeveral complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
. In the generalisation of Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
, Serre duality becomes a part of coherent duality
Coherent duality
In mathematics, coherent duality is any of a number of generalisations of Serre duality, applying to coherent sheaves, in algebraic geometry and complex manifold theory, as well as some aspects of commutative algebra that are part of the 'local' theory....
in a much broader setting. While the role of K above in general Serre duality is played by the determinant line bundle of the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
, when V is a manifold, in full generality K cannot merely be a single sheaf in the absence of some hypothesis of non-singularity on V. The formulation in full generality uses a derived category
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
and Ext functor
Ext functor
In mathematics, the Ext functors of homological algebra are derived functors of Hom functors. They were first used in algebraic topology, but are common in many areas of mathematics.- Definition and computation :...
s, to allow for the fact that K is now represented by a chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
of sheaves, namely, the dualizing complex. Nevertheless, the statement of the theorem is recognisably Serre's.