
Grothendieck spectral sequence
Encyclopedia
In mathematics
, in the field of homological algebra
, the Grothendieck spectral sequence is a technique that allows one to compute the derived functor
s of the composition of two functors , from knowledge of the derived functors of F and G.
, from knowledge of the derived functors of F and G.
If
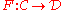
and
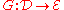
are two additive (covariant) functors between abelian categories such that is left exact
is left exact
and takes injective object
takes injective object
s of to
to  -acyclic objects of
-acyclic objects of  , then there is a spectral sequence
, then there is a spectral sequence
for each object of
of  :
:

Many spectral sequences are instances of the Grothendieck spectral sequence, for example the Leray spectral sequence
.
The exact sequence of low degrees reads
 and
and  are topological space
are topological space
s, let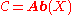 and
and 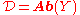 be the category of sheaves of abelian groups on X and Y, respectively and
be the category of sheaves of abelian groups on X and Y, respectively and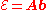 be the category of abelian groups.
be the category of abelian groups.
For a continuous map
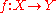
there is the (left-exact) direct image functor
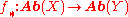 .
.
We also have the global section functors
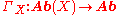 ,
,
and

Then since

and the functors
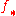
and

satisfy the hypotheses (since the direct image functor has an exact left adjoint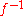 , pushforwards of injectives are injective and in particular acyclic for the global section functor), the sequence
, pushforwards of injectives are injective and in particular acyclic for the global section functor), the sequence
in this case becomes:
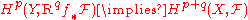
for a sheaf
 of abelian groups on
of abelian groups on  , and this is exactly the Leray spectral sequence
, and this is exactly the Leray spectral sequence
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the field of homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, the Grothendieck spectral sequence is a technique that allows one to compute the derived functor
Derived functor
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
s of the composition of two functors
 , from knowledge of the derived functors of F and G.
, from knowledge of the derived functors of F and G.If
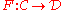
and
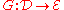
are two additive (covariant) functors between abelian categories such that
 is left exact
is left exactExact functor
In homological algebra, an exact functor is a functor, from some category to another, which preserves exact sequences. Exact functors are very convenient in algebraic calculations, roughly speaking because they can be applied to presentations of objects easily...
and
 takes injective object
takes injective objectInjective object
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in homotopy theory and in theory of model categories...
s of
 to
to  -acyclic objects of
-acyclic objects of  , then there is a spectral sequence
, then there is a spectral sequenceSpectral sequence
In homological algebra and algebraic topology, a spectral sequence is a means of computing homology groups by taking successive approximations...
for each object
 of
of  :
:
Many spectral sequences are instances of the Grothendieck spectral sequence, for example the Leray spectral sequence
Leray spectral sequence
In mathematics, the Leray spectral sequence was a pioneering example in homological algebra, introduced in 1946 by Jean Leray. The formulation was of a spectral sequence, expressing the relationship holding in sheaf cohomology between two topological spaces X and Y, and set up by a continuous...
.
The exact sequence of low degrees reads
- 0 → R1G(FA) → R1(GF)(A) → G(R1F(A)) → R2G(FA) → R2(GF)(A).
Example: the Leray spectral sequence
If and
and  are topological space
are topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s, let
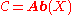 and
and 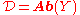 be the category of sheaves of abelian groups on X and Y, respectively and
be the category of sheaves of abelian groups on X and Y, respectively and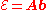 be the category of abelian groups.
be the category of abelian groups.For a continuous map
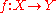
there is the (left-exact) direct image functor
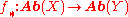 .
.We also have the global section functors
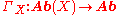 ,
,and

Then since

and the functors
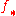
and

satisfy the hypotheses (since the direct image functor has an exact left adjoint
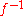 , pushforwards of injectives are injective and in particular acyclic for the global section functor), the sequence
, pushforwards of injectives are injective and in particular acyclic for the global section functor), the sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
in this case becomes:
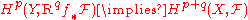
for a sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
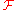 of abelian groups on
of abelian groups on  , and this is exactly the Leray spectral sequence
, and this is exactly the Leray spectral sequenceLeray spectral sequence
In mathematics, the Leray spectral sequence was a pioneering example in homological algebra, introduced in 1946 by Jean Leray. The formulation was of a spectral sequence, expressing the relationship holding in sheaf cohomology between two topological spaces X and Y, and set up by a continuous...
.

