Competitive Lotka-Volterra equations
Encyclopedia
The competitive Lotka–Volterra equations are a simple model of the population dynamics
of species competing
for some common resource
. They can be further generalised
to include trophic interactions.
. For the competition equations, the logistic equation is the basis.
The logistic population model, when used by ecologists
often takes the following form:
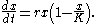
Here x is the size of the population at a given time, r is inherent per-capita growth rate, and K is the carrying capacity
.
. Thus the competitive Lotka–Volterra equations are:
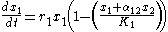

Here, α12 represents the effect species 2 has on the population of species 1 and α21 represents the effect species 1 has on the population of species 2. These values do not have to be equal. Because this is the competitive version of the model, all interactions must be harmful (competition
) and therefore all α-values are positive. Also, note that each species can have its own growth rate and carrying capacity
.
. Then the equation for any species i becomes

or, if the carrying capacity
is pulled into the interaction matrix (this doesn't actually change the equations, only how the interaction matrix is defined),
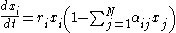
where N is the total number of interacting species. For simplicity all self-interacting terms αii are often set to 1.
(ri > 0 for all i), then some definite statements can be made about the behavior of the system.
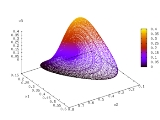
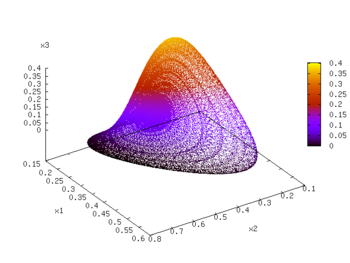 A simple 4-Dimensional example of a competitive Lotka–Volterra system has been characterized by Vano et al. Here the growth rates and interaction matrix have been set to
A simple 4-Dimensional example of a competitive Lotka–Volterra system has been characterized by Vano et al. Here the growth rates and interaction matrix have been set to
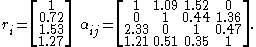
This system is chaotic and has a largest Lyapunov exponent
of 0.0203. From the theorems by Hirsch, it is one of the lowest dimensional chaotic competitive Lotka–Volterra systems. The Kaplan–Yorke dimension, a measure of the dimension
ality of the attractor
, is 2.074. This value is not a whole number, indicative of the fractal
structure inherent in a strange attractor. The coexisting equilibrium point, the point at which all derivative
s are equal to zero but that is not the origin
, can be found by inverting the interaction matrix and multiplying
by the unit column vector, and is equal to

Note that there are always 2N equilibrium points, but all others have at least one species' population equal to zero.
The eigenvalues
of the system at this point are 0.0414±0.1903i, -0.3342, and -1.0319. This point is unstable due to the positive value of the real part of the complex
eigenvalue pair. If the real part were negative, this point would be stable and the orbit would attract asymptotically. The transition between these two states, where the real part of the complex eigenvalue pair is equal to zero, is called a Hopf bifurcation
.
colonies in a field. They will compete for food strongly with the colonies located near to them, weakly with further colonies, and not at all with colonies that are far away. This doesn't mean, however, that those far colonies can be ignored. There is a transitive
effect that permeates through the system. If colony A interacts with colony B, and B with C, then C affects A through B. Therefore, if the competitive Lotka–Volterra equations are to be used for modeling such a system, they must incorporate this spatial structure.
reaction-diffusion system. It is much easier, however, to keep the format of the equations the same and instead modify the interaction matrix. For simplicity, consider a five species example where all of the species are aligned on a circle
, and each interacts only with the two neighbors on either side with strength α-1 and α1 respectively. Thus, species 3 interacts only with species 2 and 4, species 1 interacts only with species 2 and 6, etc. The interaction matrix will now be
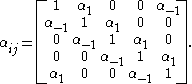
If each species is identical in its interactions with neighboring species, then each row of the matrix is just a permutation
of the first row. A simple, but non-realistic, example of this type of system has been characterized by Sprott et al. The coexisting equilibrium point for these systems has a very simple form given by the inverse
of the sum of the row
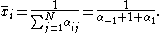
is a function
of the system f = f(x) whose existence in a system demonstrates stability
. It is often useful to imagine a Lyapunov function
as the energy of the system. If the derivative
of the function is equal to zero for some orbit
not including the equilibrium point, then that orbit
is a stable attractor
, but it must be either a limit-cycle
or n-torus
- but not a strange attractor (this is because the largest Lyapunov exponent
of a limit-cycle
and n-torus
are zero while that of a strange attractor is positive). If the derivative
is less than zero everywhere except the equilibrium point, then the equilibrium point is a stable fixed point
attractor
. When searching a dynamical system
for non-fixed point
attractor
s, the existence of a Lyapunov function
can help eliminate regions of parameter space where these dynamics are impossible.
The spatial system introduced above has a Lyapunov function
that has been explored by Wildenberg et al. If all species are identical in their spatial interactions, then the interaction matrix is circulant
. The eigenvalues
of a circulant matrix
are given by
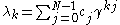
for k = 0N − 1 and where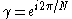 the Nth root of unity
the Nth root of unity
. Here cj is the jth value in the first row of the circulant matrix
.
The Lyapunov function
exists if the real part of the eigenvalues
are positive (Re(λk > 0 for k = 0, …, N/2). Consider the system where α-2 = a, α-1 = b, α1 = c, and α2 = d. The Lyapunov function
exists if
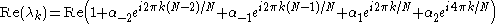
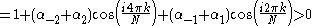
for k = 0, … ,N − 1. Now, instead of having to integrate
the system over thousands of time steps to see if any dynamics other than a fixed point
attractor
exist, one need only determine if the Lyapunov function
exists (note: the absence of the Lyapunov function
doesn't guarantee a limit-cycle
, torus
, or chaos
).
Example: Let α−2 = 0.451, α−1 = 0.5, and α2 = 0.237. If α1 = 0.5 then all eigenvalues are negative and the only attractor
is a fixed point
. If α1 = 0.852 then the real part of one of the complex eigenvalue
pair becomes positive and there is a strange attractor. The disappearance of this Lyapunov function
coincides with a Hopf bifurcation
.
 It is also possible to arrange the species into a line. The interaction matrix for this system is very similar to that of a circle except the interaction terms in the lower left and upper right of the matrix are deleted (those that describe the interactions between species 1 and N, etc.).
It is also possible to arrange the species into a line. The interaction matrix for this system is very similar to that of a circle except the interaction terms in the lower left and upper right of the matrix are deleted (those that describe the interactions between species 1 and N, etc.).
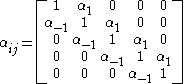
This change eliminates the Lyapunov function
described above for the system on a circle, but most likely there are other Lyapunov function
s that have not been discovered.
The eigenvalues
of the circle system plotted in the complex plane
form a trefoil
shape. The eigenvalues
from a short line form a sideways Y, but those of a long line begin to resemble the trefoil
shape of the circle. This could be due to the fact that a long line is indistinguishable from a circle to those species far from the ends.
Each site has three states, fox, bare, rabbit.
Rules are as follows:
These rules give a model like Lotka–Volterra, but the additional feature of a correlation length between regions oscillating differently. The correlation length is very long, and the model develops a wave structure.
Population dynamics
Population dynamics is the branch of life sciences that studies short-term and long-term changes in the size and age composition of populations, and the biological and environmental processes influencing those changes...
of species competing
Competition
Competition is a contest between individuals, groups, animals, etc. for territory, a niche, or a location of resources. It arises whenever two and only two strive for a goal which cannot be shared. Competition occurs naturally between living organisms which co-exist in the same environment. For...
for some common resource
Natural resource
Natural resources occur naturally within environments that exist relatively undisturbed by mankind, in a natural form. A natural resource is often characterized by amounts of biodiversity and geodiversity existent in various ecosystems....
. They can be further generalised
Generalized Lotka–Volterra equation
The generalized Lotka–Volterra equations are a set of equations which are more general than either the competitive or predator-prey examples of Lotka–Volterra types. They can be used to model direct competition and trophic relationships between an arbitrary number of species. Their...
to include trophic interactions.
Overview
The form is similar to the Lotka–Volterra equations for predation in that the equation for each species has one term for self-interaction and one term for the interaction with other species. In the equations for predation, the base population model is exponentialExponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
. For the competition equations, the logistic equation is the basis.
The logistic population model, when used by ecologists
Ecology
Ecology is the scientific study of the relations that living organisms have with respect to each other and their natural environment. Variables of interest to ecologists include the composition, distribution, amount , number, and changing states of organisms within and among ecosystems...
often takes the following form:
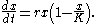
Here x is the size of the population at a given time, r is inherent per-capita growth rate, and K is the carrying capacity
Carrying capacity
The carrying capacity of a biological species in an environment is the maximum population size of the species that the environment can sustain indefinitely, given the food, habitat, water and other necessities available in the environment...
.
Two species
Given two populations, x1 and x2, with logistic dynamics, the Lotka–Volterra formulation adds an additional term to account for the species' interactionsBiological interaction
Biological interactions are the effects organisms in a community have on one another. In the natural world no organism exists in absolute isolation, and thus every organism must interact with the environment and other organisms...
. Thus the competitive Lotka–Volterra equations are:
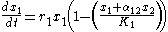

Here, α12 represents the effect species 2 has on the population of species 1 and α21 represents the effect species 1 has on the population of species 2. These values do not have to be equal. Because this is the competitive version of the model, all interactions must be harmful (competition
Competition
Competition is a contest between individuals, groups, animals, etc. for territory, a niche, or a location of resources. It arises whenever two and only two strive for a goal which cannot be shared. Competition occurs naturally between living organisms which co-exist in the same environment. For...
) and therefore all α-values are positive. Also, note that each species can have its own growth rate and carrying capacity
Carrying capacity
The carrying capacity of a biological species in an environment is the maximum population size of the species that the environment can sustain indefinitely, given the food, habitat, water and other necessities available in the environment...
.
N species
This model can be generalized to any number of species competing against each other. One can think of the populations and growth rates as vectors and the interaction αs as a matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. Then the equation for any species i becomes

or, if the carrying capacity
Carrying capacity
The carrying capacity of a biological species in an environment is the maximum population size of the species that the environment can sustain indefinitely, given the food, habitat, water and other necessities available in the environment...
is pulled into the interaction matrix (this doesn't actually change the equations, only how the interaction matrix is defined),
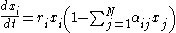
where N is the total number of interacting species. For simplicity all self-interacting terms αii are often set to 1.
Possible dynamics
The definition of a competitive Lotka-Volterra system assumes that all values in the interaction matrix are positive or 0 (αij ≥ 0 for all i,j). If it is also assumed that the population of any species will increase in the absence of competition unless the population is already at the carrying capacityCarrying capacity
The carrying capacity of a biological species in an environment is the maximum population size of the species that the environment can sustain indefinitely, given the food, habitat, water and other necessities available in the environment...
(ri > 0 for all i), then some definite statements can be made about the behavior of the system.
- The populations of all species will be bounded between 0 and 1 at all times (0 ≤ xi ≤ 1, for all i) as long as the populations started out positive.
- Smale showed that Lotka-Volterra systems that meet the above conditions and have five or more species (N ≥ 5) can exhibit any asymptoticAsymptoteIn analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
behavior, including a fixed pointFixed point (mathematics)In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
, a limit-cycleLimit-cycleIn mathematics, in the area of dynamical systems, a limit-cycle on a plane or a two-dimensional manifold is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinity or as time approaches negative infinity. Such...
, an n-torusTorusIn geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, or attractors. - Hirsch proved that all of the dynamics of the attractor occur on a manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
of dimension N-1. This basically says that the attractor cannot have dimensionDimensionIn physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
greater than N-1. Why is this important? A limit-cycleLimit-cycleIn mathematics, in the area of dynamical systems, a limit-cycle on a plane or a two-dimensional manifold is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinity or as time approaches negative infinity. Such...
cannot exist in fewer than two dimensions. A n-torusTorusIn geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
cannot exist in less than n dimensions, and finally, chaos cannot occur in less than three dimensions. So, Hirsch proved that competitive Lotka–Volterra systems cannot exhibit a limit-cycleLimit-cycleIn mathematics, in the area of dynamical systems, a limit-cycle on a plane or a two-dimensional manifold is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinity or as time approaches negative infinity. Such...
for N < 3, or any torusTorusIn geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
or chaos for N < 4. This is still in agreement with Smale that any dynamics can occur for N ≥ 5.- More specifically, Hirsch showed there is an invariantInvariant (mathematics)In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
set C that is homeomorphicHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to the (N-1)-dimensional simplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...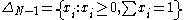
and is a global attractor of every point excluding the origin. This carrying simplex contains all of the asymptoticAsymptoteIn analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
dynamics of the system.
- More specifically, Hirsch showed there is an invariant
- To create a stable ecosystem the αij matrix must have all positive eigenvalues. For large N systems Lotka-Volterra models are either unstable or have low connectivity. Kondoh and Ackland and Gallagher have independently shown that large, stable Lotka-Volterra systems arise if the elements of αij (i.e. the features of the species) can evolve in accordance with natural selection.
4-dimensional example

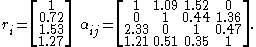
This system is chaotic and has a largest Lyapunov exponent
Lyapunov exponent
In mathematics the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories...
of 0.0203. From the theorems by Hirsch, it is one of the lowest dimensional chaotic competitive Lotka–Volterra systems. The Kaplan–Yorke dimension, a measure of the dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
ality of the attractor
Attractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
, is 2.074. This value is not a whole number, indicative of the fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
structure inherent in a strange attractor. The coexisting equilibrium point, the point at which all derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s are equal to zero but that is not the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
, can be found by inverting the interaction matrix and multiplying
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
by the unit column vector, and is equal to

Note that there are always 2N equilibrium points, but all others have at least one species' population equal to zero.
The eigenvalues
Eigenvalue, eigenvector and eigenspace
The eigenvectors of a square matrix are the non-zero vectors that, after being multiplied by the matrix, remain parallel to the original vector. For each eigenvector, the corresponding eigenvalue is the factor by which the eigenvector is scaled when multiplied by the matrix...
of the system at this point are 0.0414±0.1903i, -0.3342, and -1.0319. This point is unstable due to the positive value of the real part of the complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
eigenvalue pair. If the real part were negative, this point would be stable and the orbit would attract asymptotically. The transition between these two states, where the real part of the complex eigenvalue pair is equal to zero, is called a Hopf bifurcation
Hopf bifurcation
In the mathematical theory of bifurcations, a Hopf or Poincaré–Andronov–Hopf bifurcation, named after Henri Poincaré, Eberhard Hopf, and Aleksandr Andronov, is a local bifurcation in which a fixed point of a dynamical system loses stability as a pair of complex conjugate eigenvalues of...
.
Spatial arrangements

Background
There are many situations where the strength of species' interactions depends on the physical distance of separation. Imagine beeBee
Bees are flying insects closely related to wasps and ants, and are known for their role in pollination and for producing honey and beeswax. Bees are a monophyletic lineage within the superfamily Apoidea, presently classified by the unranked taxon name Anthophila...
colonies in a field. They will compete for food strongly with the colonies located near to them, weakly with further colonies, and not at all with colonies that are far away. This doesn't mean, however, that those far colonies can be ignored. There is a transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
effect that permeates through the system. If colony A interacts with colony B, and B with C, then C affects A through B. Therefore, if the competitive Lotka–Volterra equations are to be used for modeling such a system, they must incorporate this spatial structure.
Matrix organization
One possible way to incorporate this spatial structure is to modify the nature of the Lotka–Volterra equations to something like areaction-diffusion system. It is much easier, however, to keep the format of the equations the same and instead modify the interaction matrix. For simplicity, consider a five species example where all of the species are aligned on a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, and each interacts only with the two neighbors on either side with strength α-1 and α1 respectively. Thus, species 3 interacts only with species 2 and 4, species 1 interacts only with species 2 and 6, etc. The interaction matrix will now be
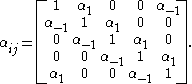
If each species is identical in its interactions with neighboring species, then each row of the matrix is just a permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of the first row. A simple, but non-realistic, example of this type of system has been characterized by Sprott et al. The coexisting equilibrium point for these systems has a very simple form given by the inverse
Inverse element
In abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
of the sum of the row
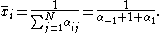
Lyapunov functions
A Lyapunov functionLyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of the system f = f(x) whose existence in a system demonstrates stability
Lyapunov stability
Various types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
. It is often useful to imagine a Lyapunov function
Lyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
as the energy of the system. If the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the function is equal to zero for some orbit
Orbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
not including the equilibrium point, then that orbit
Orbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
is a stable attractor
Attractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
, but it must be either a limit-cycle
Limit-cycle
In mathematics, in the area of dynamical systems, a limit-cycle on a plane or a two-dimensional manifold is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinity or as time approaches negative infinity. Such...
or n-torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
- but not a strange attractor (this is because the largest Lyapunov exponent
Lyapunov exponent
In mathematics the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories...
of a limit-cycle
Limit-cycle
In mathematics, in the area of dynamical systems, a limit-cycle on a plane or a two-dimensional manifold is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinity or as time approaches negative infinity. Such...
and n-torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
are zero while that of a strange attractor is positive). If the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
is less than zero everywhere except the equilibrium point, then the equilibrium point is a stable fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
attractor
Attractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
. When searching a dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
for non-fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
attractor
Attractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
s, the existence of a Lyapunov function
Lyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
can help eliminate regions of parameter space where these dynamics are impossible.
The spatial system introduced above has a Lyapunov function
Lyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
that has been explored by Wildenberg et al. If all species are identical in their spatial interactions, then the interaction matrix is circulant
Circulant matrix
In linear algebra, a circulant matrix is a special kind of Toeplitz matrix where each row vector is rotated one element to the right relative to the preceding row vector. In numerical analysis, circulant matrices are important because they are diagonalized by a discrete Fourier transform, and hence...
. The eigenvalues
Eigenvalue, eigenvector and eigenspace
The eigenvectors of a square matrix are the non-zero vectors that, after being multiplied by the matrix, remain parallel to the original vector. For each eigenvector, the corresponding eigenvalue is the factor by which the eigenvector is scaled when multiplied by the matrix...
of a circulant matrix
Circulant matrix
In linear algebra, a circulant matrix is a special kind of Toeplitz matrix where each row vector is rotated one element to the right relative to the preceding row vector. In numerical analysis, circulant matrices are important because they are diagonalized by a discrete Fourier transform, and hence...
are given by
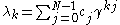
for k = 0N − 1 and where
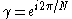 the Nth root of unity
the Nth root of unityRoot of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
. Here cj is the jth value in the first row of the circulant matrix
Circulant matrix
In linear algebra, a circulant matrix is a special kind of Toeplitz matrix where each row vector is rotated one element to the right relative to the preceding row vector. In numerical analysis, circulant matrices are important because they are diagonalized by a discrete Fourier transform, and hence...
.
The Lyapunov function
Lyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
exists if the real part of the eigenvalues
Eigenvalue, eigenvector and eigenspace
The eigenvectors of a square matrix are the non-zero vectors that, after being multiplied by the matrix, remain parallel to the original vector. For each eigenvector, the corresponding eigenvalue is the factor by which the eigenvector is scaled when multiplied by the matrix...
are positive (Re(λk > 0 for k = 0, …, N/2). Consider the system where α-2 = a, α-1 = b, α1 = c, and α2 = d. The Lyapunov function
Lyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
exists if
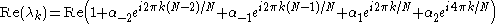
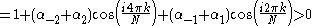
for k = 0, … ,N − 1. Now, instead of having to integrate
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
the system over thousands of time steps to see if any dynamics other than a fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
attractor
Attractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
exist, one need only determine if the Lyapunov function
Lyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
exists (note: the absence of the Lyapunov function
Lyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
doesn't guarantee a limit-cycle
Limit-cycle
In mathematics, in the area of dynamical systems, a limit-cycle on a plane or a two-dimensional manifold is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinity or as time approaches negative infinity. Such...
, torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, or chaos
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
).
Example: Let α−2 = 0.451, α−1 = 0.5, and α2 = 0.237. If α1 = 0.5 then all eigenvalues are negative and the only attractor
Attractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
is a fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
. If α1 = 0.852 then the real part of one of the complex eigenvalue
Eigenvalue, eigenvector and eigenspace
The eigenvectors of a square matrix are the non-zero vectors that, after being multiplied by the matrix, remain parallel to the original vector. For each eigenvector, the corresponding eigenvalue is the factor by which the eigenvector is scaled when multiplied by the matrix...
pair becomes positive and there is a strange attractor. The disappearance of this Lyapunov function
Lyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
coincides with a Hopf bifurcation
Hopf bifurcation
In the mathematical theory of bifurcations, a Hopf or Poincaré–Andronov–Hopf bifurcation, named after Henri Poincaré, Eberhard Hopf, and Aleksandr Andronov, is a local bifurcation in which a fixed point of a dynamical system loses stability as a pair of complex conjugate eigenvalues of...
.
Line systems and eigenvalues

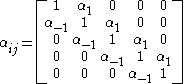
This change eliminates the Lyapunov function
Lyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
described above for the system on a circle, but most likely there are other Lyapunov function
Lyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
s that have not been discovered.
The eigenvalues
Eigenvalue, eigenvector and eigenspace
The eigenvectors of a square matrix are the non-zero vectors that, after being multiplied by the matrix, remain parallel to the original vector. For each eigenvector, the corresponding eigenvalue is the factor by which the eigenvector is scaled when multiplied by the matrix...
of the circle system plotted in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
form a trefoil
Trefoil
Trefoil is a graphic form composed of the outline of three overlapping rings used in architecture and Christian symbolism...
shape. The eigenvalues
Eigenvalue, eigenvector and eigenspace
The eigenvectors of a square matrix are the non-zero vectors that, after being multiplied by the matrix, remain parallel to the original vector. For each eigenvector, the corresponding eigenvalue is the factor by which the eigenvector is scaled when multiplied by the matrix...
from a short line form a sideways Y, but those of a long line begin to resemble the trefoil
Trefoil
Trefoil is a graphic form composed of the outline of three overlapping rings used in architecture and Christian symbolism...
shape of the circle. This could be due to the fact that a long line is indistinguishable from a circle to those species far from the ends.
Cellular automata
A rule-based automaton model is equivalent to a Lotka–Volterra system and introduces 2D space, with either periodic or fixed boundaries.Each site has three states, fox, bare, rabbit.
Rules are as follows:
- Pick a site (only stochastic updates allowed), and a neighbour.
- If fox is adjacent to rabbit, rabbit gets eaten (becomes fox with probability r). Else fox dies with probability p.
- If rabbit is adjacent to bare ground, reproduces with probability q.
- If bare ground is adjacent to anything, the thing moves into bare ground.
These rules give a model like Lotka–Volterra, but the additional feature of a correlation length between regions oscillating differently. The correlation length is very long, and the model develops a wave structure.

