
Lyapunov function
Encyclopedia
In the theory of ordinary differential equations (ODEs), Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium
of an ODE. Named after the Russia
n mathematician
Aleksandr Mikhailovich Lyapunov
, Lyapunov functions are important to stability theory
and control theory
. A similar concept appears in the theory of general state space Markov Chain
s, usually under the name Lyapunov-Foster functions.
For many classes of ODEs, the existence of Lyapunov functions is a necessary and sufficient condition for stability. Whereas there is no general technique for constructing Lyapunov functions for ODEs, in many specific cases, the construction of Lyapunov functions is known. For instance, quadratic
functions suffice for systems with one state; the solution of a particular linear matrix inequality provides Lyapunov functions for linear systems; and conservation law
s can often be used to construct Lyapunov functions for physical system
.
Informally, a Lyapunov function is a function that takes positive values everywhere except at the equilibrium in question, and decreases (or is non-increasing) along every trajectory of the ODE. The principal merit of Lyapunov function-based stability analysis of ODEs is that the actual solution (whether analytical or numerical) of the ODE is not required.
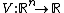
be a continuous scalar function.
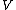 is a Lyapunov-candidate-function if it is a locally positive-definite function, i.e.
is a Lyapunov-candidate-function if it is a locally positive-definite function, i.e.
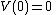
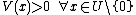
With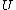 being a neighborhood region around
being a neighborhood region around 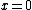
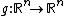
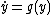
be an arbitrary autonomous dynamical system
with equilibrium point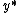 :
: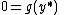
There always exists a coordinate transformation , such that:
, such that: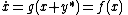
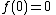
So the new system has an equilibrium point at the origin.
has an equilibrium point at the origin.
Let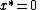
be an equilibrium of the autonomous system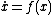
And let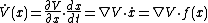
be the time derivative of the Lyapunov-candidate-function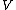 .
.
 is locally positive definite and the time derivative of the Lyapunov-candidate-function is locally negative semidefinite:
is locally positive definite and the time derivative of the Lyapunov-candidate-function is locally negative semidefinite: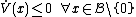
for some neighborhood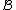 of
of  , then the equilibrium is proven to be stable
, then the equilibrium is proven to be stable
.
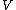 is locally positive definite and the time derivative of the Lyapunov-candidate-function is locally negative definite:
is locally positive definite and the time derivative of the Lyapunov-candidate-function is locally negative definite: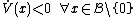
for some neighborhood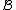 of
of  , then the equilibrium is proven to be locally asymptotically stable
, then the equilibrium is proven to be locally asymptotically stable
.
 is globally positive definite, radially unbounded and the time derivative of the Lyapunov-candidate-function is globally negative definite:
is globally positive definite, radially unbounded and the time derivative of the Lyapunov-candidate-function is globally negative definite: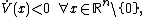
then the equilibrium is proven to be globally asymptotically stable
.
The Lyapunov-candidate function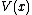 is radially unbounded if
is radially unbounded if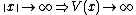 .
.
(This is also referred to as norm-coercivity.)
 :
: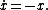
Considering that |x| is always positive around the origin it is a natural candidate to be a Lyapunov function to help us study x.
So let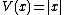 on
on  . Then,
. Then,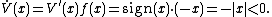
This correctly shows that the above differential equation, x, is asymptotically stable about the origin.
Equilibrium
Equilibrium is the condition of a system in which competing influences are balanced. The word may refer to:-Biology:* Equilibrioception, the sense of a balance present in human beings and other animals...
of an ODE. Named after the Russia
Russia
Russia or , officially known as both Russia and the Russian Federation , is a country in northern Eurasia. It is a federal semi-presidential republic, comprising 83 federal subjects...
n mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Aleksandr Mikhailovich Lyapunov
Aleksandr Lyapunov
Aleksandr Mikhailovich Lyapunov was a Russian mathematician, mechanician and physicist. His surname is sometimes romanized as Ljapunov, Liapunov or Ljapunow....
, Lyapunov functions are important to stability theory
Stability theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions...
and control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
. A similar concept appears in the theory of general state space Markov Chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
s, usually under the name Lyapunov-Foster functions.
For many classes of ODEs, the existence of Lyapunov functions is a necessary and sufficient condition for stability. Whereas there is no general technique for constructing Lyapunov functions for ODEs, in many specific cases, the construction of Lyapunov functions is known. For instance, quadratic
Quadratic
In mathematics, the term quadratic describes something that pertains to squares, to the operation of squaring, to terms of the second degree, or equations or formulas that involve such terms...
functions suffice for systems with one state; the solution of a particular linear matrix inequality provides Lyapunov functions for linear systems; and conservation law
Conservation law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
s can often be used to construct Lyapunov functions for physical system
Physical system
In physics, the word system has a technical meaning, namely, it is the portion of the physical universe chosen for analysis. Everything outside the system is known as the environment, which in analysis is ignored except for its effects on the system. The cut between system and the world is a free...
.
Informally, a Lyapunov function is a function that takes positive values everywhere except at the equilibrium in question, and decreases (or is non-increasing) along every trajectory of the ODE. The principal merit of Lyapunov function-based stability analysis of ODEs is that the actual solution (whether analytical or numerical) of the ODE is not required.
Definition of a Lyapunov candidate function
Let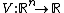
be a continuous scalar function.
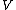 is a Lyapunov-candidate-function if it is a locally positive-definite function, i.e.
is a Lyapunov-candidate-function if it is a locally positive-definite function, i.e.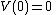
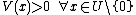
With
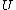 being a neighborhood region around
being a neighborhood region around 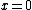
Definition of the equilibrium point of a system
Let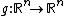
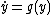
be an arbitrary autonomous dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
with equilibrium point
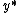 :
: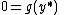
There always exists a coordinate transformation
 , such that:
, such that: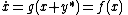
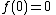
So the new system
 has an equilibrium point at the origin.
has an equilibrium point at the origin.Basic Lyapunov theorems for autonomous systems
Let
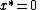
be an equilibrium of the autonomous system
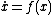
And let
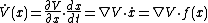
be the time derivative of the Lyapunov-candidate-function
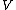 .
.Stable equilibrium
If the Lyapunov-candidate-function is locally positive definite and the time derivative of the Lyapunov-candidate-function is locally negative semidefinite:
is locally positive definite and the time derivative of the Lyapunov-candidate-function is locally negative semidefinite: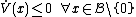
for some neighborhood
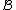 of
of  , then the equilibrium is proven to be stable
, then the equilibrium is proven to be stableStability theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions...
.
Locally asymptotically stable equilibrium
If the Lyapunov-candidate-function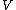 is locally positive definite and the time derivative of the Lyapunov-candidate-function is locally negative definite:
is locally positive definite and the time derivative of the Lyapunov-candidate-function is locally negative definite: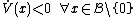
for some neighborhood
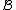 of
of  , then the equilibrium is proven to be locally asymptotically stable
, then the equilibrium is proven to be locally asymptotically stableStability theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions...
.
Globally asymptotically stable equilibrium
If the Lyapunov-candidate-function is globally positive definite, radially unbounded and the time derivative of the Lyapunov-candidate-function is globally negative definite:
is globally positive definite, radially unbounded and the time derivative of the Lyapunov-candidate-function is globally negative definite: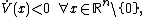
then the equilibrium is proven to be globally asymptotically stable
Stability theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions...
.
The Lyapunov-candidate function
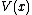 is radially unbounded if
is radially unbounded if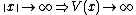 .
.(This is also referred to as norm-coercivity.)
Example
Consider the following differential equation with solution x on :
: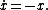
Considering that |x| is always positive around the origin it is a natural candidate to be a Lyapunov function to help us study x.
So let
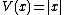 on
on  . Then,
. Then,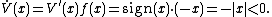
This correctly shows that the above differential equation, x, is asymptotically stable about the origin.
See also
- Ordinary differential equationOrdinary differential equationIn mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s - Control-Lyapunov functionControl-Lyapunov functionIn control theory, a control-Lyapunov function V is a generalization of the notion of Lyapunov function V used in stability analysis. The ordinary Lyapunov function is used to test whether a dynamical system is stable...
- Foster's theoremFoster's theoremIn probability theory, Foster's theorem, named after F. G. Foster, is used to draw conclusions about the positive recurrence of Markov chains with countable state spaces...
External links
- Example of determining the stability of the equilibrium solution of a system of ODEs with a Lyapunov function
- Some Lyapunov diagrams

