Generalized Lotka–Volterra equation
Encyclopedia
The generalized Lotka–Volterra equations are a set of equations which are more general than either the competitive or predator-prey examples of Lotka–Volterra types. They can be used to model direct competition and trophic relationships between an arbitrary number of species. Their dynamics can be analysed analytically to some extent. This makes them useful as a theoretical tool for modeling food web
s. However, they lack features of other ecological models such as predator preference and nonlinear functional response
s, and they cannot be used to model mutualism without allowing indefinite population growth.
The Generalised Lotka-Volterra equations model the dynamics of the populations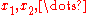
of 
biological species. Together, these populations can be considered as a vector
. They are a set of ordinary differential equation
s given by
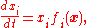
where the vector
is given by
where
is a vector and A is a matrix
known as the community matrix
.
The values of
are the intrinsic birth or death rates of the species. A positive value for 
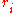means that species i is able to reproduce in the absence of any other species (for instance, because it is a plant), whereas a negative value means that its population will decline unless the appropriate other species are present (e.g. a herbivore that cannot survive without plants to eat, or a predator that cannot persist without its prey).
The values of the matrix A represent the relationships between the species. The value of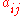
represents the effect that species j has upon species i. The effect is proportional to the populations of both species, as well as to the value of 
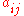. Thus, if both 
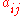and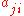 
are negative then the two species are said to be in direct competition with one another, since they each have a direct negative effect on the other's population. If 
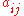is positive but 
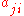is negative then species j is considered to be a predator (or parasite) on species j, since i's population grows at j's expense.
Positive values for both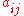
and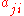 
would be considered mutualism. However, this is not often used in practice, because it can make it possible for both species' populations to grow indefinitely.
Indirect negative and positive effects are also possible. For example, if two predators eat the same prey then they compete indirectly, even though they might not have a direct competition term in the community matrix.
The diagonal terms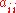
are usually taken to be negative (i.e. species i's population has a negative effect on itself). This self-limitation prevents populations from growing indefinitely.
as well as point attractors (see Hofbauer and Sigmund). As with any set of ODEs, fixed points can be found by setting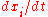
to 0 for all i, which gives
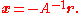
This may or may not have positive values for all the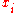
; if it does not then there is no stable attractor for which the populations of all species are positive. If there is a fixed point with all positive populations it may or may not be stable
; if it is unstable then there may or may not be a periodic or chaotic attractor
for which all the populations remain positive. In either case there can also be attractors for which some of the populations are zero and others are positive.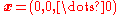
is always a fixed point, corresponding to the absence of all species.
Food web
A food web depicts feeding connections in an ecological community. Ecologists can broadly lump all life forms into one of two categories called trophic levels: 1) the autotrophs, and 2) the heterotrophs...
s. However, they lack features of other ecological models such as predator preference and nonlinear functional response
Functional response
A functional response in ecology is the intake rate of a consumer as a function of food density. It is associated with the numerical response, which is the reproduction rate of a consumer as a function of food density. Following C. S...
s, and they cannot be used to model mutualism without allowing indefinite population growth.
The Generalised Lotka-Volterra equations model the dynamics of the populations
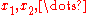of biological species. Together, these populations can be considered as a vectorVector (mathematics and physics)
In mathematics and physics, a vector is an element of a vector space. If n is a non negative integer and K is either the field of the real numbers or the field of the complex number, then K^n is naturally endowed with a structure of vector space, where K^n is the set of the ordered sequences of n...
. They are a set of ordinary differential equationOrdinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s given by
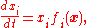
where the vector
is given bywhere
is a vector and A is a matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
known as the community matrix
Community matrix
In mathematical biology, the community matrix is the linearization of the Lotka–Volterra equation at an equilibrium point. The eigenvalues of the community matrix determine the stability of the equilibrium point....
.
Meaning of parameters
The generalised Lotka-Volterra equations can represent competition and predation, depending on the values of the parameters, as described below. They are less suitable for describing mutualism.The values of
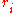are the intrinsic birth or death rates of the species. A positive value for means that species i is able to reproduce in the absence of any other species (for instance, because it is a plant), whereas a negative value means that its population will decline unless the appropriate other species are present (e.g. a herbivore that cannot survive without plants to eat, or a predator that cannot persist without its prey).The values of the matrix A represent the relationships between the species. The value of
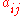represents the effect that species j has upon species i. The effect is proportional to the populations of both species, as well as to the value of 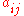. Thus, if both 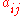and 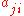are negative then the two species are said to be in direct competition with one another, since they each have a direct negative effect on the other's population. If 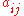is positive but 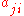is negative then species j is considered to be a predator (or parasite) on species j, since i's population grows at j's expense.Positive values for both
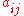and 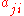would be considered mutualism. However, this is not often used in practice, because it can make it possible for both species' populations to grow indefinitely.Indirect negative and positive effects are also possible. For example, if two predators eat the same prey then they compete indirectly, even though they might not have a direct competition term in the community matrix.
The diagonal terms
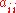are usually taken to be negative (i.e. species i's population has a negative effect on itself). This self-limitation prevents populations from growing indefinitely.Dynamics and solutions
The Generalised Lotka-Volterra equations are capable of a wide variety of dynamics, including limit cycles and chaosChaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
as well as point attractors (see Hofbauer and Sigmund). As with any set of ODEs, fixed points can be found by setting
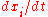to 0 for all i, which gives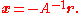This may or may not have positive values for all the
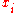; if it does not then there is no stable attractor for which the populations of all species are positive. If there is a fixed point with all positive populations it may or may not be stableLyapunov stability
Various types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
; if it is unstable then there may or may not be a periodic or chaotic attractor
Attractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
for which all the populations remain positive. In either case there can also be attractors for which some of the populations are zero and others are positive.
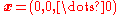is always a fixed point, corresponding to the absence of all species.See also
- Competitive Lotka–Volterra equations, based on a sigmoidal population curve (i.e., it has a carrying capacityCarrying capacityThe carrying capacity of a biological species in an environment is the maximum population size of the species that the environment can sustain indefinitely, given the food, habitat, water and other necessities available in the environment...
) - Predator–prey Lotka–Volterra equations, based on exponential population growth (i.e., no limits on reproduction ability).
- Community matrixCommunity matrixIn mathematical biology, the community matrix is the linearization of the Lotka–Volterra equation at an equilibrium point. The eigenvalues of the community matrix determine the stability of the equilibrium point....