
Classical central-force problem
Encyclopedia
In classical mechanics
, the central-force problem is to determine the motion of a particle under the influence of a single central force. A central force is a force that points from the particle directly towards (or directly away from) a fixed point in space, the center, and whose magnitude only depends on the distance of the object to the center. In many important cases, the problem can be solved analytically, i.e., in terms of well-studied functions such as trigonometric functions.
The solution of this problem is important to classical physics, since many naturally occurring forces are central. Examples include gravity and electromagnetism as described by Newton's law of universal gravitation
and Coulomb's law
, respectively. The problem is also important because some more complicated problems in classical physics (such as the two-body problem
with forces along the line connecting the two bodies) can be reduced to a central-force problem. Finally, the solution to the central-force problem often makes a good initial approximation of the true motion, as in calculating the motion of the planets in the Solar System
.
is described as an ordered pair of its x and y coordinates. of a particle moving under the influence of a central force F, either as a function of time t or as a function of the angle φ relative to the center of force and an arbitrary axis.
This two-fold definition may be expressed mathematically as follows. The center of force O can be chosen as the origin
of a coordinate system. The vector r joining O to the present position of the particle is known as the position vector. Therefore, a central force must have the mathematical form

where r is the vector magnitude |r| (the distance to the center of force) and r̂ = r/r is the corresponding unit vector. According to Newton's second law of motion
, the central force F generates a parallel acceleration a scaled by the mass m of the particleIn this article, Newton's notation for derivatives ("dot notation") is used sometimes to make the formulae easier to read; it has no other significance. In this notation, a single dot over a variable signifies its first derivative with respect to time, e.g.,

Similarly, a double dot over a variable signifies its second derivative with respect for time, e.g.,
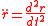
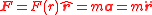
For attractive forces, F(r) is negative, because it works to reduce the distance r to the center. Conversely, for repulsive forces, F(r) is positive.
; the magnitude F(r) of a central force can always be expressed as the derivative of a time-independent potential energy
function U(r)

Thus, the total energy of the particle—the sum of its kinetic energy
and its potential energy
U—is a constant; energy is said to be conserved
. To show this, it suffices that the work W done by the force depends only on initial and final positions, not on the path taken between them.
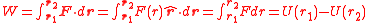
Equivalently, it suffices that the curl of the force field F is zero; using the formula for the curl in spherical coordinates
,

because the partial derivative
s are zero for a central force; the magnitude F does not depend on the angular spherical coordinates
θ and φ.
Since the scalar potential
V(r) depends only on the distance r to the origin, it has spherical symmetry. In this respect, the central-force problem is analogous to the Schwarzschild geodesics
in general relativity
and to the quantum mechanical
treatments of particles in potentials of spherical symmetry.

One solution method is to use the conservation of total energy
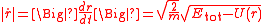
Taking the reciprocal and integrating we get:
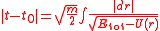
For the remainder of the article, it is assumed that the initial velocity v of the particle is not aligned with position vector r, i.e., that the angular momentum
vector L = m r × v is not zero.
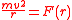
If this equation is satisfied at the initial moments, it will be satisfied at all later times; the particle will continue to move in a circle of radius r at speed v forever.
Such approximations are unnecessary, however. Newton's laws of motion allow any classical two-body problem to be converted into a corresponding exact one-body problem. To demonstrate this, let x1 and x2 be the positions of the two particles, and let r = x1 − x2 be their relative position. Then, by Newton's second law,

The final equation derives from Newton's third law
; the force of the second body on the first body (F21) is equal and opposite to the force of the first body on the second (F12). Thus, the equation of motion for r can be written in the form

where is the reduced mass
is the reduced mass
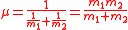
As a special case, the problem of two bodies interacting by a central force can be reduced to a central-force problem of one body.
To demonstrate this mathematically, it suffices to show that the angular momentum
of the particle is constant. This angular momentum
L is defined by the equation
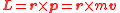
where m is the mass of the particle and p is its linear momentum.Here, the times symbol × indicates the vector cross product, not simple multiplication. Therefore, the angular momentum vector L is always perpendicular to the plane defined by the particle's position vector r and velocity vector v.If a and b are three-dimensional vectors, their vector cross product c = a × b is always perpendicular to the plane defined by a and b.
In general, the rate of change of the angular momentum L equals the net torque r × F
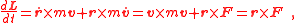
The first term m v × v is always zero, because the vector cross product
is always zero for any two vectors pointing in the same or opposite directions. However, when F is a central force, the remaining term r × F is also zero because the vectors r and F point in the same or opposite directions. Therefore, the angular momentum vector L is constant. Consequently, the particle's position r and velocity v always lie in a single plane perpendicular to L.

Taking the first derivative with respect to time yields the particle's velocity vector v

Similarly, the second derivative of the particle's position r equals its acceleration a

The velocity v and acceleration a can be expressed in terms of the radial and azimuthal unit vectors. The radial unit vector is obtained by dividing the position vector r by its magnitude r, as described above

The azimuthal unit vector is given byThis formula for the azimuthal unit vector may be verified by calculation; its magnitude equals one

and its dot-product with r equals zero

Therefore, it is a unit vector perpendicular to the radial vector r.
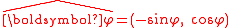
Thus, the velocity can be written as
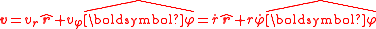
whereas the acceleration equals
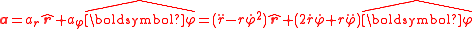
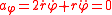
Therefore
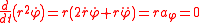
This expression in parentheses is usually denoted h

which equals the speed
v times r⊥, the component of the radius vector perpendicular to the velocity. h is the magnitude of the specific angular momentum
because it equals the magnitude L of the angular momentum divided by the mass m of the particle; in this case, the word "specific
" means "per unit mass".
For brevity, the angular speed is sometimes written ω
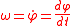
However, it should not be assumed that ω is constant. Since h is constant, ω varies with the radius r according to the formula
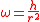
Since h is constant and r2 is positive, the angle φ changes monotonically in any central-force problem, either continuously increasing (h positive) or continuously decreasing (h negative).
, which is the rate at which area is being swept out by the particle relative to the center. Thus, the areal velocity is constant for a particle acted upon by any type of central force; this is Kepler's second law
. Conversely, if the motion under a conservative force F is planar and has constant areal velocity for all initial conditions of the radius r and velocity v, then the azimuthal acceleration aφ is always zero. Hence, by Newton's second law, F = ma, the force is a central force.
The constancy of areal velocity may be illustrated by uniform circular and linear motion. In uniform circular motion, the particle moves with constant speed v around the cricumference of a circle of radius r. Since the angular velocity ω = v/r is constant, the area swept out in a time Δt equals ω r2Δt; hence, equal areas are swept out in equal times Δt. In uniform linear motion (i.e., motion in the absence of a force, by Newton's first law of motion), the particle moves with constant velocity, that is, with constant speed v along a line. In a time Δt, the particle sweeps out an area ½vΔtr⊥ (the impact parameter
).The area of a triangle equals one half the base times its height. In this case, the base is given by vΔt and the height equals the impact parameter r⊥. The distance r⊥ does not change as the particle moves along the line; it represents the distance of closest approach of the line to the center O (the impact parameter
). Since the speed v is likewise unchanging, the areal velocity ½vr⊥ is a constant of motion; the particle sweeps out equal areas in equal times.
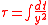
The corresponding equations of motion for ξ and η are given by
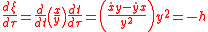
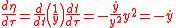
Since the rate of change of ξ is constant, its second derivative is zero
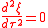
Since this is the acceleration in the ξ direction and since F=ma by Newton's second law, it follows that the force in the ξ direction is zero. Hence the force is only along the η direction, which is the criterion for a parallel-force problem. Explicitly, the acceleration in the η direction equals
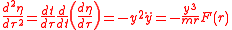
because the acceleration in the y-direction equals

Here, Fy denotes the y-component of the central force, and y/r equals the cosine of the angle between the y-axis and the radial vector r.
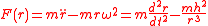
If h is not zero, the independent variable can be changed from t to φ
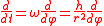
giving the new equation of motion
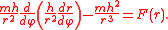
This equation becomes quasilinear on making the change of variables to the inverse radius u = 1/r
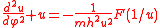
This is known as the Binet equation
. Multiplying by 2 (du/dφ) and integrating once yields the equation
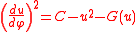
where C is a constant of integration and the function G(u) is defined by
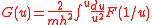
Integrating Binet's equation a second time yields the solution for φ

where φ0 is another constant of integration. A central-force problem is said to be "integrable" if this final integration can be solved in terms of known functions.

Since the total energy is constant, the rate of change of r can be calculated
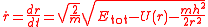
which may be converted (as before) to the derivative of r with respect to the azimuthal angle φ

Integrating and using the angular-momentum formula L=mh yields the formula

which indicates that the angular momentum contributes an effective potential energy
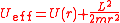
Changing the variable of integration to the inverse radius yields the integral

which expresses the above constants C = 2mEtot/L2 and G(u) = 2mU(1/u)/L2 above in terms of the total energy Etot and the potential energy U(r).
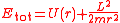
The points where this equation is satisfied are known as turning points. The orbit on either side of a turning point is symmetrical; in other words, if the azimuthal angle is defined such that φ = 0 at the turning point, then the orbit is the same in opposite directions, r(φ) = r(−φ).
If there are two turning points such that the radius r is bounded between rmin and rmax, then the motion is contained within an annulus of those radii. As the radius varies from the one turning point to the other, the change in azimuthal angle φ equals

The orbit will close upon itselfA closed orbit is one that returns to its starting position after a finite time with exactly the same velocity. Hence, it executes exactly the same motion over and over again. provided that Δφ equals a rational fraction of 2π, i.e.,
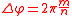
where m and n are integers. In that case, the radius oscillates exactly m times while the azimuthal angle φ makes exactly n revolutions. In general, however, Δφ will not be such a rational number
, and thus the orbit will not be closed. In that case, the particle will eventually pass arbitrarily close to every point within the annulus. Two types of central force always produce closed orbits: F(r) = αr (a linear force) and F(r) = α/r2 (an inverse square law). As shown by Bertrand, these two central forces are the only ones that guarantee closed orbits.
In general, if the angular momentum L is nonzero, the second term prevents the particle from falling into the origin, unless the effective potential energy goes to negative infinity in the limit of r going to zero. Therefore, if there is a single turning point, the orbit generally goes to infinity; the turning point corresponds to a point of minimum radius.
, many important forces follow an inverse-square law, such as gravity or electrostatics
. The general mathematical form of such inverse-square central forces is
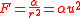
for a constant α, which is negative for an attractive force and positive for a repulsive one.
This special case of the classical central-force problem is called the Kepler problem
. For an inverse-square force, the Binet equation derived above is linear

The solution of this equation is
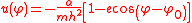
which shows that the orbit is a conic section
of eccentricity e; here, φ0 is the initial angle, and the center of force is at the focus of the conic section. Using the half-angle formula for sine, this solution can also be written as
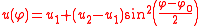
 where u1 and u2 are constants, with u2 larger than u1. The two versions of the solution are related by the equations
where u1 and u2 are constants, with u2 larger than u1. The two versions of the solution are related by the equations
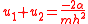
and
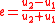
Since the sin2 function is always greater than zero, u2 is the largest possible value of u and the inverse of the smallest possible value of r, i.e., the distance of closest approach (periapsis). Since the radial distance r cannot be a negative number, neither can its inverse u; therefore, u2 must be a positive number. If u1 is also positive, it is the smallest possible value of u, which corresponds to the largest possible value of r, the distance of furthest approach (apoapsis). If u1 is zero or negative, then the smallest possible value of u is zero (the orbit goes to infinity); in this case, the only relevant values of φ are those that make u positive.
For an attractive force (α < 0), the orbit is an ellipse
, a hyperbola
or parabola
, depending on whether u1 is positive, negative, or zero, respectively; this corresponds to an eccentricity e less than one, greater than one, or equal to one. For a repulsive force (α > 0), u1 must be negative, since u2 is positive by definition and their sum is negative; hence, the orbit is a hyperbola. Naturally, if no force is present (α=0), the orbit is a straight line.
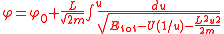
A central-force problem is said to be "integrable" if this integration can be solved in terms of known functions.
If the force is a power law, i.e., if F(r) = α rn, then u can be expressed in terms of circular functions
and/or elliptic function
s if n equals 1, -2, -3 (circular functions) and -7, -5, -4, 0, 3, 5, -3/2, -5/2, -1/3, -5/3 and -7/3 (elliptic functions). Similarly, only six possible linear combinations of power laws give solutions in terms of circular and elliptic functions
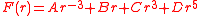
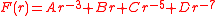
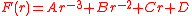

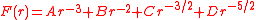
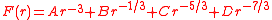
The following special cases of the first two force types always result in circular functions.
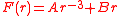

The special case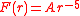
was mentioned by Newton, in corollary 1 to proposition VII of the principia, as the force implied by circular orbits passing through the point of attraction.
showed that, with adjustments in the initial conditions, the addition of such a force does not affect the radial motion of the particle, but multiplies its angular motion by a constant factor k. An extension of Newton's theorem was discovered in 2000 by Mahomed and Vawda.
Assume that a particle is moving under an arbitrary central force F1(r), and let its radius r and azimuthal angle φ be denoted as r(t) and φ1(t) as a function of time t. Now consider a second particle with the same mass m that shares the same radial motion r(t), but one whose angular speed is k times faster than that of the first particle. In other words, the azimuthal angles of the two particles are related by the equation φ2(t) = k φ1(t). Newton showed that the force acting on the second particle equals the force F1(r) acting on the first particle, plus an inverse-cube central force
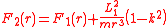
where L1 is the magnitude of the first particle's angular momentum
.
If k2 is greater than one, F2−F1 is a negative number; thus, the added inverse-cube force is attractive. Conversely, if k2 is less than one, F2−F1 is a positive number; the added inverse-cube force is repulsive. If k is an integer such as 3, the orbit of the second particle is said to be a harmonic of the first particle's orbit; by contrast, if k is the inverse of an integer, such as ⅓, the second orbit is said to be a subharmonic of the first orbit.
in his Philosophiæ Naturalis Principia Mathematica, in which Newton introduced his laws of motion. Newton used an equivalent of leapfrog integration
to convert the continuous motion to a discrete one, so that geometrical methods may be applied. In this approach, the position of the particle is considered only at evenly spaced time points. For illustration, the particle in Figure 10 is located at point A at time t = 0, at point B at time t = Δt, at point C at time t = 2Δt, and so on for all times t = nΔt, where n is an integer. The velocity is assumed to be constant between these time points. Thus, the vector rAB = rB − rA equals Δt times the velocity vector vAB (red line), whereas rBC = rC − rB equals vBCΔt (blue line). Since the velocity is constant between points, the force is assumed to act instantaneously at each new position; for example, the force acting on the particle at point B instantly changes the velocity from vAB to vBC. The difference vector Δr = rBC − rAB equals ΔvΔt (green line), where Δv = vBC − vAB is the change in velocity resulting from the force at point B. Since the acceleration a is parallel to Δv and since F = ma, the force F must be parallel to Δv and Δr. If F is a central force, it must be parallel to the vector rB from the center O to the point B (dashed green line); in that case, Δr is also parallel to rB.
If no force acts at point B, the velocity is unchanged, and the particle arrives at point K at time t = 2Δt. The areas of the triangles OAB and OBK are equal, because they share the same base (rAB) and height (r⊥). If Δr is parallel to rB, the triangles OBK and OBC are likewise equal, because they share the same base (rB) and the height is unchanged. In that case, the areas of the triangles OAB and OBC are the same, and the particle sweeps out equal areas in equal time. Conversely, if the areas of all such triangles are equal, then Δr must be parallel to rB, from which it follows that F is a central force. Thus, a particle sweeps out equal areas in equal times if and only if F is a central force.
. In polar coordinates, the Lagrangian L of a single particle in a potential energy field U(r) is given by
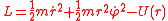
Then Lagrange's equations of motion
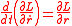
take the form

since the magnitude F(r) of the radial force equals the negative derivative of the potential energy U(r) in the radial direction.
. In polar coordinates, the Hamiltonian can be written as

Since the azimuthal angle φ does not appear in the Hamiltonian, its conjugate momentum pφ is a constant of the motion. This conjugate momentum is the magnitude L of the angular momentum, as shown by the Hamiltonian equation of motion for φ
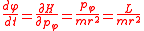
The corresponding equation of motion for r is

Taking the second derivative of r with respect to time and using Hamilton's equation of motion for pr yields the radial-force equation
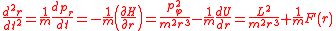
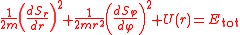
where S = Sφ(φ) + Sr(r) - Etott is Hamilton's principal function, and Etot and t represent the total energy and time, respectively. This equation may be solved by successive integrations of ordinary differential equation
s, beginning with the φ equation
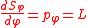
where pφ is a constant of the motion
equal to the magnitude of the angular momentum L. Thus, Sφ(φ) = Lφ and the Hamilton–Jacobi equation becomes

Integrating this equation for Sr yields
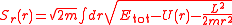
Taking the derivative of S with respect to L yields the orbital equation derived above
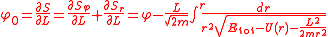
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, the central-force problem is to determine the motion of a particle under the influence of a single central force. A central force is a force that points from the particle directly towards (or directly away from) a fixed point in space, the center, and whose magnitude only depends on the distance of the object to the center. In many important cases, the problem can be solved analytically, i.e., in terms of well-studied functions such as trigonometric functions.
The solution of this problem is important to classical physics, since many naturally occurring forces are central. Examples include gravity and electromagnetism as described by Newton's law of universal gravitation
Newton's law of universal gravitation
Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...
and Coulomb's law
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
, respectively. The problem is also important because some more complicated problems in classical physics (such as the two-body problem
Two-body problem
In classical mechanics, the two-body problem is to determine the motion of two point particles that interact only with each other. Common examples include a satellite orbiting a planet, a planet orbiting a star, two stars orbiting each other , and a classical electron orbiting an atomic nucleus In...
with forces along the line connecting the two bodies) can be reduced to a central-force problem. Finally, the solution to the central-force problem often makes a good initial approximation of the true motion, as in calculating the motion of the planets in the Solar System
Solar System
The Solar System consists of the Sun and the astronomical objects gravitationally bound in orbit around it, all of which formed from the collapse of a giant molecular cloud approximately 4.6 billion years ago. The vast majority of the system's mass is in the Sun...
.
Basics
The essence of the central-force problem is to solve for the position rThroughout this article, boldface type is used to indicate that quantities such as r and F are vectors, whereas ordinary numbers are written in italics. Briefly, a vector v is a quantity that has a magnitude v (also written |v|) and a direction. Vectors are often specified by their components. For example, the position vector r = (x, y) in Cartesian coordinatesCartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
is described as an ordered pair of its x and y coordinates. of a particle moving under the influence of a central force F, either as a function of time t or as a function of the angle φ relative to the center of force and an arbitrary axis.
Definition of a central force
A central force F has two defining properties. First, it must drive particles either directly towards or directly away from a fixed point in space, the center of force, which is often labeled O. In other words, a central force must act along the line joining O with the present position of the particle. Second, a central force depends only on the distance r between O and the moving particle; it does not depend explicitly on time or other descriptors of position.This two-fold definition may be expressed mathematically as follows. The center of force O can be chosen as the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
of a coordinate system. The vector r joining O to the present position of the particle is known as the position vector. Therefore, a central force must have the mathematical form

where r is the vector magnitude |r| (the distance to the center of force) and r̂ = r/r is the corresponding unit vector. According to Newton's second law of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
, the central force F generates a parallel acceleration a scaled by the mass m of the particleIn this article, Newton's notation for derivatives ("dot notation") is used sometimes to make the formulae easier to read; it has no other significance. In this notation, a single dot over a variable signifies its first derivative with respect to time, e.g.,

Similarly, a double dot over a variable signifies its second derivative with respect for time, e.g.,
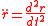
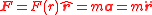
For attractive forces, F(r) is negative, because it works to reduce the distance r to the center. Conversely, for repulsive forces, F(r) is positive.
Potential energy
A central force is always a conservative forceConservative force
A conservative force is a force with the property that the work done in moving a particle between two points is independent of the path taken. Equivalently, if a particle travels in a closed loop, the net work done by a conservative force is zero.It is possible to define a numerical value of...
; the magnitude F(r) of a central force can always be expressed as the derivative of a time-independent potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
function U(r)

Thus, the total energy of the particle—the sum of its kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
and its potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
U—is a constant; energy is said to be conserved
Conservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
. To show this, it suffices that the work W done by the force depends only on initial and final positions, not on the path taken between them.
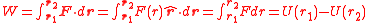
Equivalently, it suffices that the curl of the force field F is zero; using the formula for the curl in spherical coordinates
Del in cylindrical and spherical coordinates
This is a list of some vector calculus formulae of general use in working with various curvilinear coordinate systems.- Note :* This page uses standard physics notation. For spherical coordinates, \theta is the angle between the z axis and the radius vector connecting the origin to the point in...
,

because the partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s are zero for a central force; the magnitude F does not depend on the angular spherical coordinates
Spherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
θ and φ.
Since the scalar potential
Scalar potential
A scalar potential is a fundamental concept in vector analysis and physics . The scalar potential is an example of a scalar field...
V(r) depends only on the distance r to the origin, it has spherical symmetry. In this respect, the central-force problem is analogous to the Schwarzschild geodesics
Schwarzschild geodesics
In general relativity, the geodesics of the Schwarzschild metric describe the motion of particles of infinitesimal mass in the gravitational field of a central fixed mass M. The Schwarzschild geodesics have been pivotal in the validation of the Einstein's theory of general relativity...
in general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
and to the quantum mechanical
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
treatments of particles in potentials of spherical symmetry.
One-dimensional problem
If the initial velocity v of the particle is aligned with position vector r, then the motion remains forever on the line defined by r. This follows because the force—and by Newton's second law, also the acceleration a—is also aligned with r. To determine this motion, it suffices to solve the equation
One solution method is to use the conservation of total energy
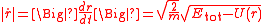
Taking the reciprocal and integrating we get:
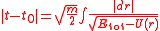
For the remainder of the article, it is assumed that the initial velocity v of the particle is not aligned with position vector r, i.e., that the angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
vector L = m r × v is not zero.
Uniform circular motion
Every central force can produce uniform circular motion, provided that the initial radius r and speed v satisfy the equation for the centripetal forceCentripetal force
Centripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens...
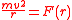
If this equation is satisfied at the initial moments, it will be satisfied at all later times; the particle will continue to move in a circle of radius r at speed v forever.
Relation to the classical two-body problem
The central-force problem concerns an ideal situation (a "one-body problem") in which a single particle is attracted or repelled from an immovable point O, the center of force. However, physical forces are generally between two bodies; and by Newton's third law, if the first body applies a force on the second, the second body applies an equal and opposite force on the first. Therefore, both bodies are accelerated if a force is present between them; there is no perfectly immovable center of force. However, if one body is overwhelmingly more massive than the other, its acceleration relative to the other may be neglected; the center of the more massive body may be treated as approximately fixed. For example, the Sun is overwhelmingly more massive than the planet Mercury; hence, the Sun may be approximated as an immovable center of force, reducing the problem to the motion of Mercury in response to the force applied by the Sun. In reality, however, the Sun also moves (albeit only slightly) in response to the force applied by the planet Mercury.Such approximations are unnecessary, however. Newton's laws of motion allow any classical two-body problem to be converted into a corresponding exact one-body problem. To demonstrate this, let x1 and x2 be the positions of the two particles, and let r = x1 − x2 be their relative position. Then, by Newton's second law,

The final equation derives from Newton's third law
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
; the force of the second body on the first body (F21) is equal and opposite to the force of the first body on the second (F12). Thus, the equation of motion for r can be written in the form

where
 is the reduced mass
is the reduced massReduced mass
Reduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. This is a quantity with the unit of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not...
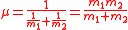
As a special case, the problem of two bodies interacting by a central force can be reduced to a central-force problem of one body.
Planar motion
The motion of a particle under a central force F always remains in the plane defined by its initial position and velocity. This may be seen by symmetry. Since the position r, velocity v and force F all lie in the same plane, there is never an acceleration perpendicular to that plane, because that would break the symmetry between "above" the plane and "below" the plane.To demonstrate this mathematically, it suffices to show that the angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
of the particle is constant. This angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
L is defined by the equation
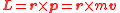
where m is the mass of the particle and p is its linear momentum.Here, the times symbol × indicates the vector cross product, not simple multiplication. Therefore, the angular momentum vector L is always perpendicular to the plane defined by the particle's position vector r and velocity vector v.If a and b are three-dimensional vectors, their vector cross product c = a × b is always perpendicular to the plane defined by a and b.
In general, the rate of change of the angular momentum L equals the net torque r × F
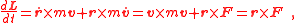
The first term m v × v is always zero, because the vector cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
is always zero for any two vectors pointing in the same or opposite directions. However, when F is a central force, the remaining term r × F is also zero because the vectors r and F point in the same or opposite directions. Therefore, the angular momentum vector L is constant. Consequently, the particle's position r and velocity v always lie in a single plane perpendicular to L.
Polar coordinates
Since the motion is planar and the force radial, it is customary to switch to polar coordinates. In these coordinates, the position vector r is represented in terms of the radial distance r and the azimuthal angle φ.
Taking the first derivative with respect to time yields the particle's velocity vector v

Similarly, the second derivative of the particle's position r equals its acceleration a

The velocity v and acceleration a can be expressed in terms of the radial and azimuthal unit vectors. The radial unit vector is obtained by dividing the position vector r by its magnitude r, as described above

The azimuthal unit vector is given byThis formula for the azimuthal unit vector may be verified by calculation; its magnitude equals one

and its dot-product with r equals zero

Therefore, it is a unit vector perpendicular to the radial vector r.
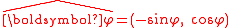
Thus, the velocity can be written as
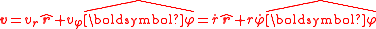
whereas the acceleration equals
Specific angular momentum
Since F = ma by Newton's second law of motion and since F is a central force, then only the radial component of the acceleration a can be non-zero; the angular component aφ must be zero
Therefore
This expression in parentheses is usually denoted h

which equals the speed
Speed
In kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...
v times r⊥, the component of the radius vector perpendicular to the velocity. h is the magnitude of the specific angular momentum
Specific relative angular momentum
The specific relative angular momentum is also known as the areal momentum .In astrodynamics, the specific relative angular momentum of two orbiting bodies is the vector product of the relative position and the relative velocity. Equivalently, it is the total angular momentum divided by the...
because it equals the magnitude L of the angular momentum divided by the mass m of the particle; in this case, the word "specific
Specific
Specific may refer to:* Specificity* Specific, a cure or therapy for a specific illnessLaw:* Specific deterrence, focussed on an individual* Specific finding, intermediate verdict used by a jury in determining the final verdict...
" means "per unit mass".
For brevity, the angular speed is sometimes written ω
However, it should not be assumed that ω is constant. Since h is constant, ω varies with the radius r according to the formula
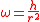
Since h is constant and r2 is positive, the angle φ changes monotonically in any central-force problem, either continuously increasing (h positive) or continuously decreasing (h negative).
Constant areal velocity
The magnitude of h also equals twice the areal velocityAreal velocity
Areal velocity is the rate at which area is swept out by a particle as it moves along a curve. In many applications, the curve lies in a plane, but in others, it is a space curve....
, which is the rate at which area is being swept out by the particle relative to the center. Thus, the areal velocity is constant for a particle acted upon by any type of central force; this is Kepler's second law
Kepler's laws of planetary motion
In astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
. Conversely, if the motion under a conservative force F is planar and has constant areal velocity for all initial conditions of the radius r and velocity v, then the azimuthal acceleration aφ is always zero. Hence, by Newton's second law, F = ma, the force is a central force.
The constancy of areal velocity may be illustrated by uniform circular and linear motion. In uniform circular motion, the particle moves with constant speed v around the cricumference of a circle of radius r. Since the angular velocity ω = v/r is constant, the area swept out in a time Δt equals ω r2Δt; hence, equal areas are swept out in equal times Δt. In uniform linear motion (i.e., motion in the absence of a force, by Newton's first law of motion), the particle moves with constant velocity, that is, with constant speed v along a line. In a time Δt, the particle sweeps out an area ½vΔtr⊥ (the impact parameter
Impact parameter
The impact parameter b is defined as the perpendicular distance between the path of a projectile and the center of the field U created by an object that the projectile is approaching...
).The area of a triangle equals one half the base times its height. In this case, the base is given by vΔt and the height equals the impact parameter r⊥. The distance r⊥ does not change as the particle moves along the line; it represents the distance of closest approach of the line to the center O (the impact parameter
Impact parameter
The impact parameter b is defined as the perpendicular distance between the path of a projectile and the center of the field U created by an object that the projectile is approaching...
). Since the speed v is likewise unchanging, the areal velocity ½vr⊥ is a constant of motion; the particle sweeps out equal areas in equal times.
Equivalent parallel force field
By a transformation of variables, any central-force problem can be converted into an equivalent parallel-force problem.A parallel-force problem is one in which the force is exactly zero along one direction. In place of the ordinary x and y Cartesian coordinates, two new position variables ξ = x/y and η = 1/y are defined, as is a new time coordinate τ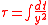
The corresponding equations of motion for ξ and η are given by
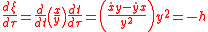
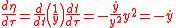
Since the rate of change of ξ is constant, its second derivative is zero
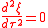
Since this is the acceleration in the ξ direction and since F=ma by Newton's second law, it follows that the force in the ξ direction is zero. Hence the force is only along the η direction, which is the criterion for a parallel-force problem. Explicitly, the acceleration in the η direction equals
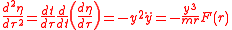
because the acceleration in the y-direction equals

Here, Fy denotes the y-component of the central force, and y/r equals the cosine of the angle between the y-axis and the radial vector r.
Binet equation
Since a central force F acts only along the radius, only the radial component of the acceleration is nonzero. By Newton's second law of motion, the magnitude of F equals the mass m of the particle times the magnitude of its radial acceleration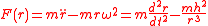
If h is not zero, the independent variable can be changed from t to φ
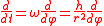
giving the new equation of motion
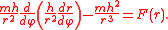
This equation becomes quasilinear on making the change of variables to the inverse radius u = 1/r
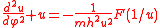
This is known as the Binet equation
Binet equation
The Binet equation, derived by Jacques Philippe Marie Binet, provides the form of a central force given the shape of the orbital motion in plane polar coordinates. The equation can also be used to derive the shape of the orbit for a given force law, but this usually involves the solution to a...
. Multiplying by 2 (du/dφ) and integrating once yields the equation
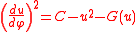
where C is a constant of integration and the function G(u) is defined by
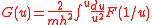
Integrating Binet's equation a second time yields the solution for φ

where φ0 is another constant of integration. A central-force problem is said to be "integrable" if this final integration can be solved in terms of known functions.
Orbit of the particle
The total energy of the system Etot equals the sum of the potential energy and the kinetic energy
Since the total energy is constant, the rate of change of r can be calculated
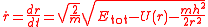
which may be converted (as before) to the derivative of r with respect to the azimuthal angle φ

Integrating and using the angular-momentum formula L=mh yields the formula

which indicates that the angular momentum contributes an effective potential energy
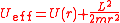
Changing the variable of integration to the inverse radius yields the integral

which expresses the above constants C = 2mEtot/L2 and G(u) = 2mU(1/u)/L2 above in terms of the total energy Etot and the potential energy U(r).
Turning points and closed orbits
The rate of change of r is zero whenever the effective potential energy equals the total energy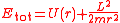
The points where this equation is satisfied are known as turning points. The orbit on either side of a turning point is symmetrical; in other words, if the azimuthal angle is defined such that φ = 0 at the turning point, then the orbit is the same in opposite directions, r(φ) = r(−φ).
If there are two turning points such that the radius r is bounded between rmin and rmax, then the motion is contained within an annulus of those radii. As the radius varies from the one turning point to the other, the change in azimuthal angle φ equals

The orbit will close upon itselfA closed orbit is one that returns to its starting position after a finite time with exactly the same velocity. Hence, it executes exactly the same motion over and over again. provided that Δφ equals a rational fraction of 2π, i.e.,
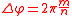
where m and n are integers. In that case, the radius oscillates exactly m times while the azimuthal angle φ makes exactly n revolutions. In general, however, Δφ will not be such a rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
, and thus the orbit will not be closed. In that case, the particle will eventually pass arbitrarily close to every point within the annulus. Two types of central force always produce closed orbits: F(r) = αr (a linear force) and F(r) = α/r2 (an inverse square law). As shown by Bertrand, these two central forces are the only ones that guarantee closed orbits.
In general, if the angular momentum L is nonzero, the second term prevents the particle from falling into the origin, unless the effective potential energy goes to negative infinity in the limit of r going to zero. Therefore, if there is a single turning point, the orbit generally goes to infinity; the turning point corresponds to a point of minimum radius.
Kepler problem
In classical physicsClassical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
, many important forces follow an inverse-square law, such as gravity or electrostatics
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
. The general mathematical form of such inverse-square central forces is
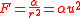
for a constant α, which is negative for an attractive force and positive for a repulsive one.
This special case of the classical central-force problem is called the Kepler problem
Kepler problem
In classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force F that varies in strength as the inverse square of the distance r between them. The force may be either attractive or repulsive...
. For an inverse-square force, the Binet equation derived above is linear

The solution of this equation is
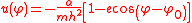
which shows that the orbit is a conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
of eccentricity e; here, φ0 is the initial angle, and the center of force is at the focus of the conic section. Using the half-angle formula for sine, this solution can also be written as
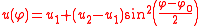

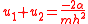
and
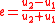
Since the sin2 function is always greater than zero, u2 is the largest possible value of u and the inverse of the smallest possible value of r, i.e., the distance of closest approach (periapsis). Since the radial distance r cannot be a negative number, neither can its inverse u; therefore, u2 must be a positive number. If u1 is also positive, it is the smallest possible value of u, which corresponds to the largest possible value of r, the distance of furthest approach (apoapsis). If u1 is zero or negative, then the smallest possible value of u is zero (the orbit goes to infinity); in this case, the only relevant values of φ are those that make u positive.
For an attractive force (α < 0), the orbit is an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
, a hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
or parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
, depending on whether u1 is positive, negative, or zero, respectively; this corresponds to an eccentricity e less than one, greater than one, or equal to one. For a repulsive force (α > 0), u1 must be negative, since u2 is positive by definition and their sum is negative; hence, the orbit is a hyperbola. Naturally, if no force is present (α=0), the orbit is a straight line.
Central forces with exact solutions
The Binet equation for u(φ) can be solved numerically for nearly any central force F(1/u). However, only a handful of forces result in formulae for u in terms of known functions. As derived above, the solution for φ can be expressed as an integral over u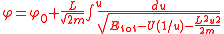
A central-force problem is said to be "integrable" if this integration can be solved in terms of known functions.
If the force is a power law, i.e., if F(r) = α rn, then u can be expressed in terms of circular functions
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
and/or elliptic function
Elliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
s if n equals 1, -2, -3 (circular functions) and -7, -5, -4, 0, 3, 5, -3/2, -5/2, -1/3, -5/3 and -7/3 (elliptic functions). Similarly, only six possible linear combinations of power laws give solutions in terms of circular and elliptic functions
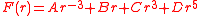
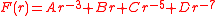
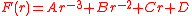

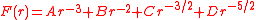
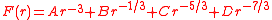
The following special cases of the first two force types always result in circular functions.
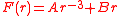

The special case
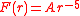
was mentioned by Newton, in corollary 1 to proposition VII of the principia, as the force implied by circular orbits passing through the point of attraction.
Newton's theorem of revolving orbits
The term r−3 occurs in all the force laws above, indicating that the addition of the inverse-cube force does not influence the solubility of the problem in terms of known functions. NewtonIsaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
showed that, with adjustments in the initial conditions, the addition of such a force does not affect the radial motion of the particle, but multiplies its angular motion by a constant factor k. An extension of Newton's theorem was discovered in 2000 by Mahomed and Vawda.
Assume that a particle is moving under an arbitrary central force F1(r), and let its radius r and azimuthal angle φ be denoted as r(t) and φ1(t) as a function of time t. Now consider a second particle with the same mass m that shares the same radial motion r(t), but one whose angular speed is k times faster than that of the first particle. In other words, the azimuthal angles of the two particles are related by the equation φ2(t) = k φ1(t). Newton showed that the force acting on the second particle equals the force F1(r) acting on the first particle, plus an inverse-cube central force
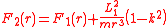
where L1 is the magnitude of the first particle's angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
.
If k2 is greater than one, F2−F1 is a negative number; thus, the added inverse-cube force is attractive. Conversely, if k2 is less than one, F2−F1 is a positive number; the added inverse-cube force is repulsive. If k is an integer such as 3, the orbit of the second particle is said to be a harmonic of the first particle's orbit; by contrast, if k is the inverse of an integer, such as ⅓, the second orbit is said to be a subharmonic of the first orbit.
Historical development
Newton's derivation
The classical central-force problem was solved geometrically by Isaac NewtonIsaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
in his Philosophiæ Naturalis Principia Mathematica, in which Newton introduced his laws of motion. Newton used an equivalent of leapfrog integration
Leapfrog integration
Leapfrog integration is a simple method for numerically integrating differential equations of the form\ddot x=F,or equivalently of the form\dot v=F,\;\dot x \equiv v,particularly in the case of a dynamical system of classical mechanics...
to convert the continuous motion to a discrete one, so that geometrical methods may be applied. In this approach, the position of the particle is considered only at evenly spaced time points. For illustration, the particle in Figure 10 is located at point A at time t = 0, at point B at time t = Δt, at point C at time t = 2Δt, and so on for all times t = nΔt, where n is an integer. The velocity is assumed to be constant between these time points. Thus, the vector rAB = rB − rA equals Δt times the velocity vector vAB (red line), whereas rBC = rC − rB equals vBCΔt (blue line). Since the velocity is constant between points, the force is assumed to act instantaneously at each new position; for example, the force acting on the particle at point B instantly changes the velocity from vAB to vBC. The difference vector Δr = rBC − rAB equals ΔvΔt (green line), where Δv = vBC − vAB is the change in velocity resulting from the force at point B. Since the acceleration a is parallel to Δv and since F = ma, the force F must be parallel to Δv and Δr. If F is a central force, it must be parallel to the vector rB from the center O to the point B (dashed green line); in that case, Δr is also parallel to rB.
If no force acts at point B, the velocity is unchanged, and the particle arrives at point K at time t = 2Δt. The areas of the triangles OAB and OBK are equal, because they share the same base (rAB) and height (r⊥). If Δr is parallel to rB, the triangles OBK and OBC are likewise equal, because they share the same base (rB) and the height is unchanged. In that case, the areas of the triangles OAB and OBC are the same, and the particle sweeps out equal areas in equal time. Conversely, if the areas of all such triangles are equal, then Δr must be parallel to rB, from which it follows that F is a central force. Thus, a particle sweeps out equal areas in equal times if and only if F is a central force.
Lagrangian mechanics
The formula for the radial force may also be obtained using Lagrangian mechanicsLagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
. In polar coordinates, the Lagrangian L of a single particle in a potential energy field U(r) is given by
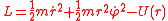
Then Lagrange's equations of motion
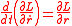
take the form

since the magnitude F(r) of the radial force equals the negative derivative of the potential energy U(r) in the radial direction.
Hamiltonian mechanics
The radial force formula may also be derived using Hamiltonian mechanicsHamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
. In polar coordinates, the Hamiltonian can be written as

Since the azimuthal angle φ does not appear in the Hamiltonian, its conjugate momentum pφ is a constant of the motion. This conjugate momentum is the magnitude L of the angular momentum, as shown by the Hamiltonian equation of motion for φ
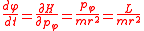
The corresponding equation of motion for r is

Taking the second derivative of r with respect to time and using Hamilton's equation of motion for pr yields the radial-force equation
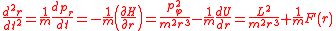
Hamilton-Jacobi equation
The orbital equation can be derived directly from the Hamilton-Jacobi equation. Adopting the radial distance r and the azimuthal angle φ as the coordinates, the Hamilton-Jacobi equation for a central-force problem can be written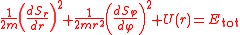
where S = Sφ(φ) + Sr(r) - Etott is Hamilton's principal function, and Etot and t represent the total energy and time, respectively. This equation may be solved by successive integrations of ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s, beginning with the φ equation
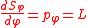
where pφ is a constant of the motion
Constant of motion
In mechanics, a constant of motion is a quantity that is conserved throughout the motion, imposing in effect a constraint on the motion. However, it is a mathematical constraint, the natural consequence of the equations of motion, rather than a physical constraint...
equal to the magnitude of the angular momentum L. Thus, Sφ(φ) = Lφ and the Hamilton–Jacobi equation becomes

Integrating this equation for Sr yields
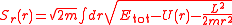
Taking the derivative of S with respect to L yields the orbital equation derived above
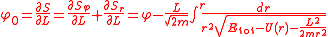
See also
- Schwarzschild geodesicsSchwarzschild geodesicsIn general relativity, the geodesics of the Schwarzschild metric describe the motion of particles of infinitesimal mass in the gravitational field of a central fixed mass M. The Schwarzschild geodesics have been pivotal in the validation of the Einstein's theory of general relativity...
, for a central-force problem in general relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics... - Particle in a spherically symmetric potential, the quantum-mechanical analog of the central-force problem
- Hydrogen-like atomHydrogen-like atomA hydrogen-like ion is any atomic nucleus with one electron and thus is isoelectronic with hydrogen. Except for the hydrogen atom itself , these ions carry the positive charge e, where Z is the atomic number of the atom. Examples of hydrogen-like ions are He+, Li2+, Be3+ and B4+...
, the Kepler problem in quantum mechanicsQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
External links
- Two-body Central Force Problems by D. E. Gary of the New Jersey Institute of TechnologyNew Jersey Institute of TechnologyNew Jersey Institute of Technology is a public research university in Newark, New Jersey. It is often also referred to as Newark College of Engineering ....
- Motion in a Central-Force Field by A. Brizard of Saint Michael's CollegeSaint Michael's CollegeSaint Michael's College is a private, residential liberal arts Catholic college. The campus is located in Colchester, Vermont. It was founded in 1904 by the Society of Saint Edmund, a French order of Catholic priests.-History:...
- Motion under the Influence of a Central Force by G. W. Collins, II of Case Western Reserve UniversityCase Western Reserve UniversityCase Western Reserve University is a private research university located in Cleveland, Ohio, USA...
- Video lecture by W. H. G. Lewin of the Massachusetts Institute of TechnologyMassachusetts Institute of TechnologyThe Massachusetts Institute of Technology is a private research university located in Cambridge, Massachusetts. MIT has five schools and one college, containing a total of 32 academic departments, with a strong emphasis on scientific and technological education and research.Founded in 1861 in...

