Binet equation
Encyclopedia
The Binet equation, derived by Jacques Philippe Marie Binet
, provides the form of a central force given the shape of the orbital motion in plane polar coordinates. The equation can also be used to derive the shape of the orbit for a given force law, but this usually involves the solution to a second order nonlinear ordinary differential equation
. A unique solution is impossible in the case of circular motion
about the center of force.
as a function of angle 
. For the Binet equation, the orbital shape is instead more concisely described by the reciprocal 
as a function of 
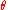. Define the specific angular momentum as 
where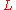 
is the angular momentum
and
is the mass. The Binet equation is
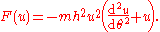
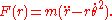
The conservation of angular momentum requires that
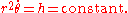
Derivatives of
with respect to time may be rewritten as derivatives of 
with respect to angle.
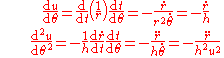
Combine all of the above and we have
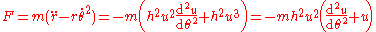
of calculating the orbit of an inverse square law may be read off from the Binet equation as the solution to the differential equation
If the angle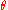
is measured from the periapsis, then the general solution for the orbit expressed in (reciprocal) polar coordinates is
The above polar equation describes conic section
s, with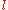
the semi-latus rectum and 
the orbital eccentricity
.
The relativistic equation derived for Schwarzschild coordinates
is
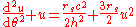
where
is the speed of light
and
is the Schwarzschild radius
. And for Reissner–Nordström metric we will obtain
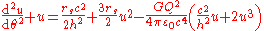
where
is the electric charge
and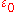
is the vacuum permittivity.
) around a focus of the ellipse
?
Differentiating twice the above polar equation for an ellipse gives
The force law is therefore
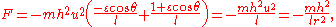
which is the anticipated inverse square law. Matching the orbital \text{constant}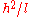
to physical values like 
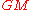or :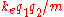
reproduces Newton's law of universal gravitation
or Coulomb's law
, respectively.
The effective force for Schwarzschild coordinates is
.
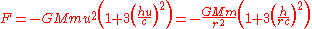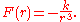
The shapes of the orbits of an inverse cube law are known as Cotes spirals. The Binet equation shows that the orbits must be solutions to the equation
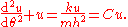
The differential equation has three kinds of solutions, in analogy to the different conic sections of the Kepler problem. When
, the solution is the epispiral, including the pathological case of a straight line when 
. When 
, the solution is the hyperbolic spiral
. When
the solution is Poinsot's spiral.
is
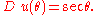
Differentiating
twice and making use of the Pythagorean identity gives
The force law is thus
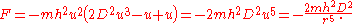
Note that solving the general inverse problem, i.e. constructing the orbits of an attractive
force law, is a considerably more difficult problem because it is equivalent to solving
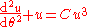
which is a second order nonlinear differential equation.
Jacques Philippe Marie Binet
Jacques Philippe Marie Binet was a French mathematician, physicist and astronomer born in Rennes; he died in Paris, France, in 1856. He made significant contributions to number theory, and the mathematical foundations of matrix algebra which would later lead to important contributions by Cayley...
, provides the form of a central force given the shape of the orbital motion in plane polar coordinates. The equation can also be used to derive the shape of the orbit for a given force law, but this usually involves the solution to a second order nonlinear ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
. A unique solution is impossible in the case of circular motion
Circular motion
In physics, circular motion is rotation along a circular path or a circular orbit. It can be uniform, that is, with constant angular rate of rotation , or non-uniform, that is, with a changing rate of rotation. The rotation around a fixed axis of a three-dimensional body involves circular motion of...
about the center of force.
Equation
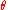The shape of an orbit is often conveniently described in terms of relative distance as a function of angle . For the Binet equation, the orbital shape is instead more concisely described by the reciprocal as a function of . Define the specific angular momentum as where 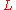is the angular momentumAngular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
and
is the mass. The Binet equation is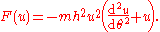Derivation
Newton's Second Law for a purely central force is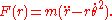The conservation of angular momentum requires that
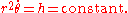
Derivatives of
with respect to time may be rewritten as derivatives of with respect to angle.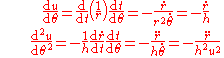Combine all of the above and we have
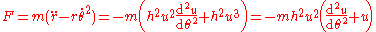
Kepler problem
The traditional Kepler problemKepler problem
In classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force F that varies in strength as the inverse square of the distance r between them. The force may be either attractive or repulsive...
of calculating the orbit of an inverse square law may be read off from the Binet equation as the solution to the differential equation
If the angle
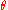is measured from the periapsis, then the general solution for the orbit expressed in (reciprocal) polar coordinates isThe above polar equation describes conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
s, with
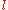the semi-latus rectum and the orbital eccentricityOrbital eccentricity
The orbital eccentricity of an astronomical body is the amount by which its orbit deviates from a perfect circle, where 0 is perfectly circular, and 1.0 is a parabola, and no longer a closed orbit...
.
The relativistic equation derived for Schwarzschild coordinates
Schwarzschild coordinates
In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric...
is
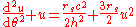
where
is the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
and
is the Schwarzschild radiusSchwarzschild radius
The Schwarzschild radius is the distance from the center of an object such that, if all the mass of the object were compressed within that sphere, the escape speed from the surface would equal the speed of light...
. And for Reissner–Nordström metric we will obtain
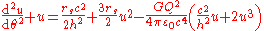
where
is the electric chargeElectric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
and
is the vacuum permittivity.Inverse Kepler problem
Consider the inverse Kepler problem. What kind of force law produces a noncircular elliptical orbit (or more generally a noncircular conic sectionConic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
) around a focus of the ellipse
Focus (geometry)
In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...
?
Differentiating twice the above polar equation for an ellipse gives
The force law is therefore
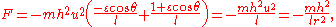
which is the anticipated inverse square law. Matching the orbital \text{constant}
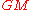to physical values like or :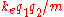 reproduces Newton's law of universal gravitationNewton's law of universal gravitation
Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...
or Coulomb's law
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
, respectively.
The effective force for Schwarzschild coordinates is
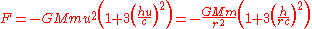.Cotes spirals
An inverse cube force law has the form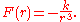The shapes of the orbits of an inverse cube law are known as Cotes spirals. The Binet equation shows that the orbits must be solutions to the equation
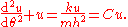
The differential equation has three kinds of solutions, in analogy to the different conic sections of the Kepler problem. When
, the solution is the epispiral, including the pathological case of a straight line when . When , the solution is the hyperbolic spiralHyperbolic spiral
thumb|200px|right|Hyperbolic spiral for a=2A hyperbolic spiral is a transcendental plane curve also known as a reciprocal spiral. A hyperbolic spiral is the opposite of an Archimedean spiral and are a type of Cotes' spiral.It has the polar equation:...
. When
the solution is Poinsot's spiral.Off-axis circular motion
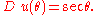
Although the Binet equation fails to give a unique force law for circular motion about the center of force, the equation can provide a force law when the circle's center and the center of force do not coincide. Consider for example a circular orbit that passes directly through the center of force. A (reciprocal) polar equation for such a circular orbit of diameter isDifferentiating
twice and making use of the Pythagorean identity givesThe force law is thus
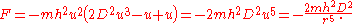
Note that solving the general inverse problem, i.e. constructing the orbits of an attractive
force law, is a considerably more difficult problem because it is equivalent to solving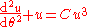which is a second order nonlinear differential equation.
See also
- Bohr–Sommerfeld quantization#Relativistic orbit
- Classical central-force problemClassical central-force problemIn classical mechanics, the central-force problem is to determine the motion of a particle under the influence of a single central force. A central force is a force that points from the particle directly towards a fixed point in space, the center, and whose magnitude only depends on the distance...
- General relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
- Two-body problem in general relativity