
Triangular prism
Encyclopedia
In geometry
, a triangular prism is a three-sided prism
; it is a polyhedron
made of a triangular
base, a translated
copy, and 3 faces joining corresponding sides.
Equivalently, it is a pentahedron
of which two faces are parallel, while the surface normal
s of the other three are in the same plane (which is not necessarily parallel to the base planes). These three faces are parallelogram
s. All cross-sections parallel to the base faces are the same triangle.
or, more generally, a uniform polyhedron
if the base faces are equilateral triangle
s, and the other three faces are squares
. It can be seen as a truncated
trigonal hosohedron, represented by Schläfli symbol t{2,3}. Alternately it can be seen as the Cartesian product
of a triangle and a line segment
, and represented by the product {3}x{}. The dual
of a triangular prism is a triangular bipyramid.
The symmetry group
of a right 3-sided prism with triangular base is D3h
of order 12. The rotation group
is D3 of order 6. The symmetry group does not contain inversion.
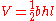
where b is the triangle base length, h is the triangle height, and l is the length between the triangles.
and [n,3] Coxeter group
symmetry.
There are 9 uniform honeycombs that include triangular prism cells:
The triangular prism exists as cells of a number of four-dimensional uniform polychora
, including:
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a triangular prism is a three-sided prism
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
; it is a polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
made of a triangular
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
base, a translated
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
copy, and 3 faces joining corresponding sides.
Equivalently, it is a pentahedron
Pentahedron
In geometry, a pentahedron is a polyhedron with five faces. Since there are no face-transitive polyhedra with five sides and there are two distinct topological types, this term is less frequently used than tetrahedron or octahedron....
of which two faces are parallel, while the surface normal
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
s of the other three are in the same plane (which is not necessarily parallel to the base planes). These three faces are parallelogram
Parallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
s. All cross-sections parallel to the base faces are the same triangle.
As a semiregular (or uniform) polyhedron
A right triangular prism is semiregularSemiregular polyhedron
The term semiregular polyhedron is used variously by different authors.In its original definition, it is a polyhedron with regular faces and a symmetry group which is transitive on its vertices, which is more commonly referred to today as a uniform polyhedron...
or, more generally, a uniform polyhedron
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
if the base faces are equilateral triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s, and the other three faces are squares
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
. It can be seen as a truncated
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
trigonal hosohedron, represented by Schläfli symbol t{2,3}. Alternately it can be seen as the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of a triangle and a line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
, and represented by the product {3}x{}. The dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
of a triangular prism is a triangular bipyramid.
The symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of a right 3-sided prism with triangular base is D3h
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
of order 12. The rotation group
Rotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
is D3 of order 6. The symmetry group does not contain inversion.
Volume
The volume of any prism is the product of the area of the base and the distance between the two bases. In this case the base is a triangle so we simply need to compute the area of the triangle and multiply this by the length of the prism: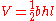
where b is the triangle base length, h is the triangle height, and l is the length between the triangles.
Related polyhedra
It is related to the following sequence of uniform truncated polyhedra and tilings with 3.2n.2n a vertex configurationVertex configuration
In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron...
and [n,3] Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
symmetry.
 3.4.4 |
 3.6.6 Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
 3.8.8 Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... |
 3.10.10 Truncated dodecahedron In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges.- Geometric relations :... |
 3.12.12 Truncated hexagonal tiling In geometry, the truncated hexagonal tiling is a semiregular tiling of the Euclidean plane. There are 2 dodecagons and one triangle on each vertex.... |
 3.14.14 Order-3 truncated heptagonal tiling In geometry, the Truncated order-3 heptagonal tiling is a semiregular tiling of the hyperbolic plane. There is one triangle and two tetrakaidecagons on each vertex... |
 3.16.16 |
3.∞.∞ |
Related polytopes
There are 4 uniform compounds of triangular prisms:- Compound of four triangular prismsCompound of four triangular prismsThis uniform polyhedron compound is a chiral symmetric arrangement of 4 triangular prisms, aligned with the axes of three-fold rotational symmetry of an octahedron.- Cartesian coordinates :...
, compound of eight triangular prismsCompound of eight triangular prismsThis uniform polyhedron compound is a symmetric arrangement of 8 triangular prisms, aligned in pairs with the axes of three-fold rotational symmetry of an octahedron. It results from composing the two enantiomorphs of the compound of 4 triangular prisms....
, compound of ten triangular prismsCompound of ten triangular prismsThis uniform polyhedron compound is a chiral symmetric arrangement of 10 triangular prisms, aligned with the axes of three-fold rotational symmetry of an icosahedron.- Relatde polyhedra :...
, compound of twenty triangular prismsCompound of twenty triangular prismsThis uniform polyhedron compound is a symmetric arrangement of 20 triangular prisms, aligned in pairs with the axes of three-fold rotational symmetry of an icosahedron.It results from composing the two enantiomorphs of the compound of 10 triangular prisms...
.
There are 9 uniform honeycombs that include triangular prism cells:
- Gyroelongated alternated cubic honeycombGyroelongated alternated cubic honeycombThe gyroelongated alternated cubic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed of octahedra, triangular prisms, and tetrahedra in a ratio of 1:2:2....
, elongated alternated cubic honeycombElongated alternated cubic honeycombThe elongated alternated cubic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed of octahedra, triangular prisms, and tetrahedra in a ratio of 1:2:2....
, gyrated triangular prismatic honeycombGyrated triangular prismatic honeycombThe gyrated triangular prismatic honeycomb is a space-filling tessellation in Euclidean 3-space made up of triangular prisms. It is vertex-uniform with 12 triangular prisms per vertex....
, snub square prismatic honeycombSnub square prismatic honeycombThe snub square prismatic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed of cubes and triangular prisms in a ratio of 1:2.It is constructed from a Snub square tiling extruded into prisms....
, triangular prismatic honeycombTriangular prismatic honeycombThe triangular prismatic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed entirely of triangular prisms.It is constructed from a triangular tiling extruded into prisms.It is one of 28 convex uniform honeycombs....
, triangular-hexagonal prismatic honeycombTriangular-hexagonal prismatic honeycombThe triangular-hexagonal prismatic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed of hexagonal prisms and triangular prisms in a ratio of 1:2.It is constructed from a trihexagonal tiling extruded into prisms....
, truncated hexagonal prismatic honeycombTruncated hexagonal prismatic honeycombThe truncated hexagonal prismatic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed of dodecagonal prisms, and triangular prisms in a ratio of 1:2....
, rhombitriangular-hexagonal prismatic honeycombRhombitriangular-hexagonal prismatic honeycombThe rhombitriangular-hexagonal prismatic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed of hexagonal prisms, cubes, and triangular prisms in a ratio of 1:3:2....
, snub triangular-hexagonal prismatic honeycombSnub triangular-hexagonal prismatic honeycombThe Snub triangular-hexagonal prismatic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed of hexagonal prisms and triangular prisms in a ratio of 1:8....
, elongated triangular prismatic honeycombElongated triangular prismatic honeycombThe elongated triangular prismatic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed of cubes and triangular prisms in a ratio of 1:2.It is constructed from an elongated triangular tiling extruded into prisms....
The triangular prism exists as cells of a number of four-dimensional uniform polychora
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
, including:
| tetrahedral prism |
octahedral prism Octahedral prism In geometry, a octahedral prism is a convex uniform polychoron . This polychoron has 10 polyhedral cells: 2 octahedra connected by 8 triangular prisms.- Related polytopes :... |
cuboctahedral prism Cuboctahedral prism In geometry, a cuboctahedral prism is a convex uniform polychoron . This polychoron has 16 polyhedral cells: 2 cuboctahedra connected by 8 triangular prisms, and 6 cubes.... |
icosahedral prism Icosahedral prism In geometry, an icosahedral prism is a convex uniform polychoron . This polychoron has 22 polyhedral cells: 2 icosahedra connected by 20 triangular prisms. It has 70 faces: 30 squares and 40 triangles... |
icosidodecahedral prism Icosidodecahedral prism In geometry, an icosidodecahedral prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of parallel Platonic solids or Archimedean solids.... |
Truncated dodecahedral prism Truncated dodecahedral prism In geometry, a truncated dodecahedral prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.- Alternative names :* Truncated-dodecahedral dyadic prism... |
||
 |
 |
 |
 |
 |
 |
||
| Rhombi-cosidodecahedral prism Rhombicosidodecahedral prism In geometry, a rhombicosidodecahedral prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.- Alternative names :* rhombicosidodecahedral dyadic prism... |
Rhombi-cuboctahedral prism Rhombicuboctahedral prism In geometry, a rhombicuboctahedral prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.- Alternative names :* rhombicuboctahedral dyadic prism In... |
Truncated cubic prism Truncated cubic prism In geometry, a truncated cubic prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.- Alternative names :* Truncated-cubic hyperprism* Truncated-cubic... |
Snub dodecahedral prism Snub dodecahedral prism In geometry, a snub dodecahedral prism is a convex uniform polychoron .It is one of 18 convex uniform polyhedral prisms created by using uniform prisms to connect pairs of Platonic solids or Archimedean solids in parallel hyperplanes.- Alternative names :* Snub-icosidodecahedral dyadic prism In... |
n-gonal antiprismatic prism Uniform antiprismatic prism In 4-dimensional geometry, a uniform antiprismatic prism is a uniform polychoron with two uniform antiprism cells in two parallel 3-space hyperplanes, connected by uniform prisms cells between pairs of faces.... |
|||
 |
 |
 |
 |
 |
|||
| Cantellated 5-cell Cantellated 5-cell In four-dimensional geometry, a cantellated 5-cell is a convex uniform polychoron, being a cantellation of the regular 5-cell.There are 2 unique degrees of runcinations of the 5-cell including with permutations truncations.... |
Cantitruncated 5-cell |
Runcinated 5-cell |
Runcitruncated 5-cell |
Cantellated tesseract Cantellated tesseract In four-dimensional geometry, a cantellated tesseract is a convex uniform polychoron, being a cantellation of the regular tesseract.There are four degrees of cantellations of the tesseract including with permutations truncations... |
Cantitruncated tesseract |
Runcinated tesseract Runcinated tesseract In four-dimensional geometry, a runcinated tesseract is a convex uniform polychoron, being a runcination of the regular tesseract.... |
Runcitruncated tesseract |
| Cantellated 24-cell Cantellated 24-cell In four-dimensional geometry, a cantellated 24-cell is a convex uniform polychoron, being a cantellation of the regular 24-cell.There are 2 unique degrees of runcinations of the 24-cell including with permutations truncations.... |
Cantitruncated 24-cell |
Runcinated 24-cell Runcinated 24-cell In four-dimensional geometry, a runcinated 24-cell is a convex uniform polychoron, being a runcination of the regular 24-cell.... |
Runcitruncated 24-cell |
Cantellated 120-cell Cantellated 120-cell In four-dimensional geometry, a cantellated 120-cell is a convex uniform polychoron, being a cantellation of the regular 120-cell.... |
Cantitruncated 120-cell |
Runcinated 120-cell Runcinated 120-cell In four-dimensional geometry, a runcinated 120-cell is a convex uniform polychoron, being a runcination of the regular 120-cell.... |
Runcitruncated 120-cell |

