
Johnson solid
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a Johnson solid is a strictly convex polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
, each face of which is a regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
, but which is not uniform
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
, i.e., not a Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
, Archimedean solid
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
, prism
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
or antiprism
Antiprism
In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
. There is no requirement that each face must be the same polygon, or that the same polygons join around each vertex. An example of a Johnson solid is the square-based pyramid
Pyramid (geometry)
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle. It is a conic solid with polygonal base....
with equilateral
Equilateral
In geometry, an equilateral polygon is a polygon which has all sides of the same length.For instance, an equilateral triangle is a triangle of equal edge lengths...
sides (J1
Square pyramid
In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it will have C4v symmetry.- Johnson solid :...
); it has 1 square face and 4 triangular faces.
As in any strictly convex solid, at least three faces meet at every vertex, and the total of their angles is less than 360 degrees. Since a regular polygon has angles at least 60 degrees, it follows that at most five faces meet at any vertex. The pentagonal pyramid
Pentagonal pyramid
In geometry, a pentagonal pyramid is a pyramid with a pentagonal base upon which are erected five triangular faces that meet at a point . Like any pyramid, it is self-dual....
(J2) is an example that actually has a degree-5 vertex.
Although there is no obvious restriction that any given regular polygon cannot be a face of a Johnson solid, it turns out that the faces of Johnson solids always have 3, 4, 5, 6, 8, or 10 sides.
In 1966, Norman Johnson published a list which included all 92 solids, and gave them their names and numbers. He did not prove that there were only 92, but he did conjecture that there were no others. Victor Zalgaller
Victor Zalgaller
Victor Abramovich Zalgaller is a mathematician in the fields of geometry and optimization. He is best known for his results on convex polyhedra, linear and dynamic programming, isoperimetry, and differential geometry....
in 1969 proved that Johnson's list was complete.
Of the Johnson solids, the elongated square gyrobicupola
Elongated square gyrobicupola
In geometry, the elongated square gyrobicupola or pseudorhombicuboctahedron is one of the Johnson solids . The 92 Johnson solids were named and described by Norman Johnson in 1966.- Relation to Rhombicuboctahedron :...
(J37) is unique in being locally vertex-uniform: there are 4 faces at each vertex, and their arrangement is always the same: 3 squares and 1 triangle. However, it is not vertex-transitive, as it has different isometry at different vertices, making it a Johnson solid rather than an Archimedean solid
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
.
Names
The names are listed below and are more descriptive than they sound. Most of the Johnson solids can be constructed from the first few (pyramidsPyramid (geometry)
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle. It is a conic solid with polygonal base....
, cupola
Cupola (geometry)
In geometry, a cupola is a solid formed by joining two polygons, one with twice as many edges as the other, by an alternating band of triangles and rectangles...
e, and rotunda
Pentagonal rotunda
In geometry, the pentagonal rotunda is one of the Johnson solids . It can be seen as half an icosidodecahedron.The 92 Johnson solids were named and described by Norman Johnson in 1966.-Formulae:...
), together with the Platonic
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
and Archimedean
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
solids, prism
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
s, and antiprism
Antiprism
In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
s.
- Bi- means that two copies of the solid in question are joined base-to-base. For cupolae and rotundae, they can be joined so that like faces (ortho-) or unlike faces (gyro-) meet. In this nomenclature, an octahedronOctahedronIn geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
would be a square bipyramid, a cuboctahedronCuboctahedronIn geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
would be a triangular gyrobicupola, and an icosidodecahedronIcosidodecahedronIn geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
would be a pentagonal gyrobirotunda. - Elongated means that a prism has been joined to the base of the solid in question or between the bases of the solids in question. A rhombicuboctahedronRhombicuboctahedronIn geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles...
would be an elongated square orthobicupola. - Gyroelongated means that an antiprismAntiprismIn geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
has been joined to the base of the solid in question or between the bases of the solids in question. An icosahedronIcosahedronIn geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
would be a gyroelongated pentagonal bipyramid. - Augmented means that a pyramid or cupola has been joined to a face of the solid in question.
- Diminished means that a pyramid or cupola has been removed from the solid in question.
- GyrateGyrationIn geometry, a gyration is a type of rotation.The center of a rotational symmetry is a rotation point. A rotation point that does not lie on a mirror is called a gyration point. A rotocenter is a rotation point with an integral number of rotational symmetries.-See also:*Terms starting with...
means that a cupola on the solid in question has been rotated so that different edges match up, as in the difference between ortho- and gyrobicupolae.
The last three operations — augmentation, diminution, and gyration — can be performed more than once on a large enough solid. We add bi- to the name of the operation to indicate that it has been performed twice. (A bigyrate solid has had two of its cupolae rotated.) We add tri- to indicate that it has been performed three times. (A tridiminished solid has had three of its pyramids or cupolae removed.)
Sometimes, bi- alone is not specific enough. We must distinguish between a solid that has had two parallel faces altered and one that has had two oblique faces altered. When the faces altered are parallel, we add para- to the name of the operation. (A parabiaugmented solid has had two parallel faces augmented.) When they are not, we add meta- to the name of the operation. (A metabiaugmented solid has had 2 oblique faces augmented.)
Enumeration
| Jn | Solid name | Net Net (polyhedron) In geometry the net of a polyhedron is an arrangement of edge-joined polygons in the plane which can be folded to become the faces of the polyhedron... |
Image | V | E | F | F3 | F4 | F5 | F6 | F8 | F10 | Symmetry group |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Square pyramid Square pyramid In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it will have C4v symmetry.- Johnson solid :... |
 |
 |
5 | 8 | 5 | 4 | 1 | C4v | ||||
| 2 | Pentagonal pyramid Pentagonal pyramid In geometry, a pentagonal pyramid is a pyramid with a pentagonal base upon which are erected five triangular faces that meet at a point . Like any pyramid, it is self-dual.... |
 |
 |
6 | 10 | 6 | 5 | 1 | C5v | ||||
| 3 | Triangular cupola Triangular cupola In geometry, the triangular cupola is one of the Johnson solids . It can be seen as half a cuboctahedron.The 92 Johnson solids were named and described by Norman Johnson in 1966.-Formulae:... |
 |
 |
9 | 15 | 8 | 4 | 3 | 1 | C3v | |||
| 4 | Square cupola Square cupola In geometry, the square cupola, sometimes called lesser dome, is one of the Johnson solids . It can be obtained as a slice of the rhombicuboctahedron... |
 |
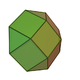 |
12 | 20 | 10 | 4 | 5 | 1 | C4v | |||
| 5 | Pentagonal cupola Pentagonal cupola In geometry, the pentagonal cupola is one of the Johnson solids . It can be obtained as a slice of the rhombicosidodecahedron.The 92 Johnson solids were named and described by Norman Johnson in 1966.... |
 |
 |
15 | 25 | 12 | 5 | 5 | 1 | 1 | C5v | ||
| 6 | Pentagonal rotunda Pentagonal rotunda In geometry, the pentagonal rotunda is one of the Johnson solids . It can be seen as half an icosidodecahedron.The 92 Johnson solids were named and described by Norman Johnson in 1966.-Formulae:... |
 |
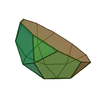 |
20 | 35 | 17 | 10 | 6 | 1 | C5v | |||
| 7 | Elongated triangular pyramid Elongated triangular pyramid In geometry, the elongated triangular pyramid is one of the Johnson solids . Norman Johnson discovered elongated triangular pyramids. As the name suggests, it can be constructed by elongating a tetrahedron by attaching a triangular prism to its base... (or elongated tetrahedron) |
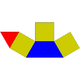 |
 |
7 | 12 | 7 | 4 | 3 | C3v | ||||
| 8 | Elongated square pyramid Elongated square pyramid In geometry, the elongated square pyramid is one of the Johnson solids . As the name suggests, it can be constructed by elongating a square pyramid by attaching a cube to its square base... (or augmented cube) |
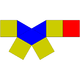 |
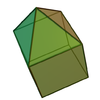 |
9 | 16 | 9 | 4 | 5 | C4v | ||||
| 9 | Elongated pentagonal pyramid Elongated pentagonal pyramid In geometry, the elongated pentagonal pyramid is one of the Johnson solids . As the name suggests, it can be constructed by elongating a pentagonal pyramid by attaching a pentagonal prism to its base.... |
 |
 |
11 | 20 | 11 | 5 | 5 | 1 | C5v | |||
| 10 | Gyroelongated square pyramid Gyroelongated square pyramid In geometry, the gyroelongated square pyramid is one of the Johnson solids . As its name suggests, it can be constructed by taking a square pyramid and "gyroelongating" it, which in this case involves joining a square antiprism to its base.... |
 |
 |
9 | 20 | 13 | 12 | 1 | C4v | ||||
| 11 | Gyroelongated pentagonal pyramid Gyroelongated pentagonal pyramid In geometry, the gyroelongated pentagonal pyramid is one of the Johnson solids . As its name suggests, it is formed by taking a pentagonal pyramid and "gyroelongating" it, which in this case involves joining a pentagonal antiprism to its base.... (or diminished icosahedron) |
 |
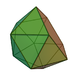 |
11 | 25 | 16 | 15 | 1 | C5v | ||||
| 12 | Triangular bipyramid |  |
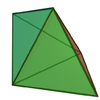 |
5 | 9 | 6 | 6 | D3h | |||||
| 13 | Pentagonal bipyramid |  |
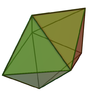 |
7 | 15 | 10 | 10 | D5h | |||||
| 14 | Elongated triangular bipyramid |  |
 |
8 | 15 | 9 | 6 | 3 | D3h | ||||
| 15 | Elongated square bipyramid (or biaugmented cube) |
 |
 |
10 | 20 | 12 | 8 | 4 | D4h | ||||
| 16 | Elongated pentagonal bipyramid |  |
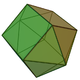 |
12 | 25 | 15 | 10 | 5 | D5h | ||||
| 17 | Gyroelongated square bipyramid |  |
 |
10 | 24 | 16 | 16 | D4d | |||||
| 18 | Elongated triangular cupola Elongated triangular cupola In geometry, the elongated triangular cupola is one of the Johnson solids . As the name suggests, it can be constructed by elongating a triangular cupola by attaching a hexagonal prism to its base.... |
 |
 |
15 | 27 | 14 | 4 | 9 | 1 | C3v | |||
| 19 | Elongated square cupola Elongated square cupola In geometry, the elongated square cupola is one of the Johnson solids . As the name suggests, it can be constructed by elongating a square cupola by attaching an octagonal prism to its base... (diminished rhombicuboctahedron) |
 |
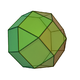 |
20 | 36 | 18 | 4 | 13 | 1 | C4v | |||
| 20 | Elongated pentagonal cupola Elongated pentagonal cupola In geometry, the elongated pentagonal cupola is one of the Johnson solids . As the name suggests, it can be constructed by elongating a pentagonal cupola by attaching a decagonal prism to its base... |
 |
 |
25 | 45 | 22 | 5 | 15 | 1 | 1 | C5v | ||
| 21 | Elongated pentagonal rotunda Elongated pentagonal rotunda In geometry, the elongated pentagonal rotunda is one of the Johnson solids . As the name suggests, it can be constructed by elongating a pentagonal rotunda by attaching a decagonal prism to its base... |
 |
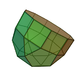 |
30 | 55 | 27 | 10 | 10 | 6 | 1 | C5v | ||
| 22 | Gyroelongated triangular cupola Gyroelongated triangular cupola In geometry, the gyroelongated triangular cupola is one of the Johnson solids . As the name suggests, it can be constructed by gyroelongating a triangular cupola by attaching a hexagonal antiprism to its base. It can also be seen as a gyroelongated triangular bicupola with one triangular cupola... |
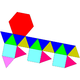 |
 |
15 | 33 | 20 | 16 | 3 | 1 | C3v | |||
| 23 | Gyroelongated square cupola Gyroelongated square cupola In geometry, the gyroelongated square cupola is one of the Johnson solids . As the name suggests, it can be constructed by gyroelongating a square cupola by attaching an octagonal antiprism to its base... |
 |
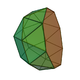 |
20 | 44 | 26 | 20 | 5 | 1 | C4v | |||
| 24 | Gyroelongated pentagonal cupola Gyroelongated pentagonal cupola In geometry, the gyroelongated pentagonal cupola is one of the Johnson solids . As the name suggests, it can be constructed by gyroelongating a pentagonal cupola by attaching a decagonal antiprism to its base... |
 |
 |
25 | 55 | 32 | 25 | 5 | 1 | 1 | C5v | ||
| 25 | Gyroelongated pentagonal rotunda Gyroelongated pentagonal rotunda In geometry, the gyroelongated pentagonal rotunda is one of the Johnson solids . As the name suggests, it can be constructed by gyroelongating a pentagonal rotunda by attaching a decagonal antiprism to its base... |
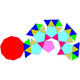 |
 |
30 | 65 | 37 | 30 | 6 | 1 | C5v | |||
| 26 | Gyrobifastigium Gyrobifastigium In geometry, the gyrobifastigium is the 26th Johnson solid . It can be constructed by joining two face-regular triangular prisms along corresponding square faces, giving a half-turn to one prism.... |
 |
 |
8 | 14 | 8 | 4 | 4 | D2d | ||||
| 27 | Triangular orthobicupola Triangular orthobicupola In geometry, the triangular orthobicupola is one of the Johnson solids . As the name suggests, it can be constructed by attaching two triangular cupolas along their bases... (gyrate cuboctahedron) |
 |
 |
12 | 24 | 14 | 8 | 6 | D3h | ||||
| 28 | Square orthobicupola Square orthobicupola In geometry, the square orthobicupola is one of the Johnson solids . As the name suggests, it can be constructed by joining two square cupolae along their octagonal bases, matching like faces... |
 |
 |
16 | 32 | 18 | 8 | 10 | D4h | ||||
| 29 | Square gyrobicupola Square gyrobicupola In geometry, the square gyrobicupola is one of the Johnson solids . Like the square orthobicupola , it can be obtained by joining two square cupolae along their bases... |
 |
 |
16 | 32 | 18 | 8 | 10 | D4d | ||||
| 30 | Pentagonal orthobicupola Pentagonal orthobicupola In geometry, the pentagonal orthobicupola is one of the Johnson solids . As the name suggests, it can be constructed by joining two pentagonal cupolae along their decagonal bases, matching like faces... |
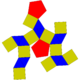 |
 |
20 | 40 | 22 | 10 | 10 | 2 | D5h | |||
| 31 | Pentagonal gyrobicupola Pentagonal gyrobicupola In geometry, the pentagonal gyrobicupola is one of the Johnson solids . Like the pentagonal orthobicupola , it can be obtained by joining two pentagonal cupolae along their bases... |
 |
 |
20 | 40 | 22 | 10 | 10 | 2 | D5d | |||
| 32 | Pentagonal orthocupolarotunda Pentagonal orthocupolarotunda In geometry, the pentagonal orthocupolarotunda is one of the Johnson solids . As the name suggests, it can be constructed by joining a pentagonal cupola and a pentagonal rotunda along their decagonal bases, matching the pentagonal faces... |
 |
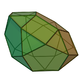 |
25 | 50 | 27 | 15 | 5 | 7 | C5v | |||
| 33 | Pentagonal gyrocupolarotunda Pentagonal gyrocupolarotunda In geometry, the pentagonal gyrocupolarotunda is one of the Johnson solids . Like the pentagonal orthocupolarotunda , it can be constructed by joining a pentagonal cupola and a pentagonal rotunda along their decagonal bases... |
 |
 |
25 | 50 | 27 | 15 | 5 | 7 | C5v | |||
| 34 | Pentagonal orthobirotunda Pentagonal orthobirotunda In geometry, the pentagonal orthobirotunda is one of the Johnson solids . As the name suggests, it can be constructed by joining two pentagonal rotundae along their decagonal faces, matching like faces... (gyrate icosidodecahedron) |
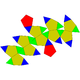 |
 |
30 | 60 | 32 | 20 | 12 | D5h | ||||
| 35 | Elongated triangular orthobicupola Elongated triangular orthobicupola In geometry, the elongated triangular orthobicupola is one of the Johnson solids . As the name suggests, it can be constructed by elongating a triangular orthobicupola by inserting a hexagonal prism between its two halves... |
 |
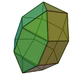 |
18 | 36 | 20 | 8 | 12 | D3h | ||||
| 36 | Elongated triangular gyrobicupola Elongated triangular gyrobicupola In geometry, the elongated triangular gyrobicupola is one of the Johnson solids . As the name suggests, it can be constructed by elongating a "triangular gyrobicupola," or cuboctahedron, by inserting a hexagonal prism between its two halves, which are congruent triangular cupolae... |
 |
 |
18 | 36 | 20 | 8 | 12 | D3d | ||||
| 37 | Elongated square gyrobicupola Elongated square gyrobicupola In geometry, the elongated square gyrobicupola or pseudorhombicuboctahedron is one of the Johnson solids . The 92 Johnson solids were named and described by Norman Johnson in 1966.- Relation to Rhombicuboctahedron :... (gyrate rhombicuboctahedron) |
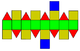 |
 |
24 | 48 | 26 | 8 | 18 | D4d | ||||
| 38 | Elongated pentagonal orthobicupola Elongated pentagonal orthobicupola In geometry, the elongated pentagonal orthobicupola is one of the Johnson solids . As the name suggests, it can be constructed by elongating a pentagonal orthobicupola by inserting a decagonal prism between its two congruent halves... |
 |
 |
30 | 60 | 32 | 10 | 20 | 2 | D5h | |||
| 39 | Elongated pentagonal gyrobicupola Elongated pentagonal gyrobicupola In geometry, the elongated pentagonal gyrobicupola is one of the Johnson solids . As the name suggests, it can be constructed by elongating a pentagonal gyrobicupola by inserting a decagonal prism between its congruent halves... |
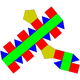 |
 |
30 | 60 | 32 | 10 | 20 | 2 | D5d | |||
| 40 | Elongated pentagonal orthocupolarotunda Elongated pentagonal orthocupolarotunda In geometry, the elongated pentagonal orthocupolarotunda is one of the Johnson solids . As the name suggests, it can be constructed by elongating a pentagonal orthocupolarotunda by inserting a decagonal prism between its halves... |
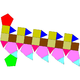 |
 |
35 | 70 | 37 | 15 | 15 | 7 | C5v | |||
| 41 | Elongated pentagonal gyrocupolarotunda Elongated pentagonal gyrocupolarotunda In geometry, the elongated pentagonal gyrocupolarotunda is one of the Johnson solids . As the name suggests, it can be constructed by elongating a pentagonal gyrocupolarotunda by inserting a decagonal prism between its halves... |
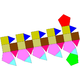 |
 |
35 | 70 | 37 | 15 | 15 | 7 | C5v | |||
| 42 | Elongated pentagonal orthobirotunda Elongated pentagonal orthobirotunda In geometry, the elongated pentagonal orthobirotunda is one of the Johnson solids . As the name suggests, it can be constructed by elongating a pentagonal orthobirotunda by inserting a decagonal prism between its congruent halves... |
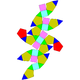 |
 |
40 | 80 | 42 | 20 | 10 | 12 | D5h | |||
| 43 | Elongated pentagonal gyrobirotunda Elongated pentagonal gyrobirotunda In geometry, the elongated pentagonal gyrobirotunda is one of the Johnson solids . As the name suggests, it can be constructed by elongating a "pentagonal gyrobirotunda," or icosidodecahedron , by inserting a decagonal prism between its congruent halves... |
 |
 |
40 | 80 | 42 | 20 | 10 | 12 | D5d | |||
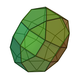
| 44 | Gyroelongated triangular bicupola Gyroelongated triangular bicupola In geometry, the gyroelongated triangular bicupola is one of the Johnson solids . As the name suggests, it can be constructed by gyroelongating a triangular bicupola by inserting a hexagonal antiprism between its congruent halves.The gyroelongated triangular bicupola is one of five Johnson solids... (2 chiral forms) |
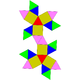 |
 |
18 | 42 | 26 | 20 | 6 | D3 | ||||
| 45 | Gyroelongated square bicupola Gyroelongated square bicupola In geometry, the gyroelongated square bicupola is one of the Johnson solids . As the name suggests, it can be constructed by gyroelongating a square bicupola by inserting an octagonal antiprism between its congruent halves.... (2 chiral forms) |
 |
 |
24 | 56 | 34 | 24 | 10 | D4 | ||||
| 46 | Gyroelongated pentagonal bicupola Gyroelongated pentagonal bicupola In geometry, the gyroelongated pentagonal bicupola is one of the Johnson solids . As the name suggests, it can be constructed by gyroelongating a pentagonal bicupola by inserting a decagonal antiprism between its congruent halves.... (2 chiral forms) |
 |
 |
30 | 70 | 42 | 30 | 10 | 2 | D5 | |||
| 47 | Gyroelongated pentagonal cupolarotunda Gyroelongated pentagonal cupolarotunda In geometry, the gyroelongated pentagonal cupolarotunda is one of the Johnson solids . As the name suggests, it can be constructed by gyroelongating a pentagonal cupolarotunda by inserting a decagonal antiprism between its two halves.The gyroelongated pentagonal cupolarotunda is one of five... (2 chiral forms) |
 |
 |
35 | 80 | 47 | 35 | 5 | 7 | C5 | |||
| 48 | Gyroelongated pentagonal birotunda Gyroelongated pentagonal birotunda In geometry, the gyroelongated pentagonal birotunda is one of the Johnson solids . As the name suggests, it can be constructed by gyroelongating a pentagonal birotunda by inserting a decagonal antiprism between its two halves.The gyroelongated pentagonal birotunda is one of five Johnson solids... (2 chiral forms) |
 |
 |
40 | 90 | 52 | 40 | 12 | D5 | ||||
| 49 | Augmented triangular prism Augmented triangular prism In geometry, the augmented triangular prism is one of the Johnson solids . As the name suggests, it can be constructed by augmenting a triangular prism by attaching a square pyramid to one of its equatorial faces... |
 |
 |
7 | 13 | 8 | 6 | 2 | C2v | ||||
| 50 | Biaugmented triangular prism Biaugmented triangular prism In geometry, the biaugmented triangular prism is one of the Johnson solids . As the name suggests, it can be constructed by augmenting a triangular prism by attaching square pyramids to two of its equatorial faces.... |
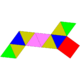 |
 |
8 | 17 | 11 | 10 | 1 | C2v | ||||
| 51 | Triaugmented triangular prism Triaugmented triangular prism In geometry, the triaugmented triangular prism is one of the Johnson solids . As the name suggests, it can be constructed by attaching square pyramids to each of the three equatorial faces of the triangular prism... |
 |
 |
9 | 21 | 14 | 14 | D3h | |||||
| 52 | Augmented pentagonal prism Augmented pentagonal prism In geometry, the augmented pentagonal prism is one of the Johnson solids . As the name suggests, it can be constructed by augmenting a pentagonal prism by attaching a square pyramid to one of its equatorial faces.... |
 |
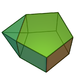 |
11 | 19 | 10 | 4 | 4 | 2 | C2v | |||
| 53 | Biaugmented pentagonal prism Biaugmented pentagonal prism In geometry, the biaugmented pentagonal prism is one of the Johnson solids . As the name suggests, it can be constructed by doubly augmenting a pentagonal prism by attaching square pyramids to two of its nonadjacent equatorial faces... |
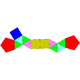 |
 |
12 | 23 | 13 | 8 | 3 | 2 | C2v | |||
| 54 | Augmented hexagonal prism Augmented hexagonal prism In geometry, the augmented hexagonal prism is one of the Johnson solids . As the name suggests, it can be constructed by augmenting a hexagonal prism by attaching a square pyramid to one of its equatorial faces.... |
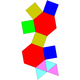 |
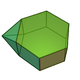 |
13 | 22 | 11 | 4 | 5 | 2 | C2v | |||
| 55 | Parabiaugmented hexagonal prism Parabiaugmented hexagonal prism In geometry, the parabiaugmented hexagonal prism is one of the Johnson solids .The 92 Johnson solids were named and described by Norman Johnson in 1966.-External links:**... |
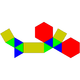 |
 |
14 | 26 | 14 | 8 | 4 | 2 | D2h | |||
| 56 | Metabiaugmented hexagonal prism Metabiaugmented hexagonal prism In geometry, the metabiaugmented hexagonal prism is one of the Johnson solids .The 92 Johnson solids were named and described by Norman Johnson in 1966.-External links:**... |
 |
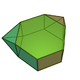 |
14 | 26 | 14 | 8 | 4 | 2 | C2v | |||
| 57 | Triaugmented hexagonal prism Triaugmented hexagonal prism In geometry, the triaugmented hexagonal prism is one of the Johnson solids .The 92 Johnson solids were named and described by Norman Johnson in 1966.-External links:**... |
 |
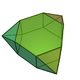 |
15 | 30 | 17 | 12 | 3 | 2 | D3h | |||
| 58 | Augmented dodecahedron Augmented dodecahedron In geometry, the augmented dodecahedron is one of the Johnson solids , consisting of a dodecahedron with a pentagonal pyramid attached to one of the faces... |
 |
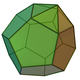 |
21 | 35 | 16 | 5 | 11 | C5v | ||||
| 59 | Parabiaugmented dodecahedron Parabiaugmented dodecahedron In geometry, the parabiaugmented dodecahedron is one of the Johnson solids . It can be seen as a dodecahedron with two pentagonal pyramids attached to opposite faces... |
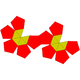 |
 |
22 | 40 | 20 | 10 | 10 | D5d | ||||
| 60 | Metabiaugmented dodecahedron Metabiaugmented dodecahedron In geometry, the metabiaugmented dodecahedron is one of the Johnson solids . It can be viewed as a dodecahedron with two pentagonal pyramids attached to two faces that are separated by one face... |
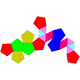 |
 |
22 | 40 | 20 | 10 | 10 | C2v | ||||
| 61 | Triaugmented dodecahedron Triaugmented dodecahedron In geometry, the triaugmented dodecahedron is one of the Johnson solids .The 92 Johnson solids were named and described by Norman Johnson in 1966.-External links:**... |
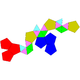 |
 |
23 | 45 | 24 | 15 | 9 | C3v | ||||
| 62 | Metabidiminished icosahedron Metabidiminished icosahedron In geometry, the metabidiminished icosahedron is one of the Johnson solids . The name refers to one way of constructing it, by removing two pentagonal pyramids from a regular icosahedron, replacing two sets of five triangular faces of the icosahedron with two adjacent pentagonal faces... |
 |
 |
10 | 20 | 12 | 10 | 2 | C2v | ||||
| 63 | Tridiminished icosahedron Tridiminished icosahedron In geometry, the tridiminished icosahedron is one of the Johnson solids .The 92 Johnson solids were named and described by Norman Johnson in 1966.- Related polytopes :... |
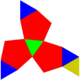 |
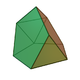 |
9 | 15 | 8 | 5 | 3 | C3v | ||||
| 64 | Augmented tridiminished icosahedron Augmented tridiminished icosahedron In geometry, the augmented tridiminished icosahedron is one of theJohnson solids .It can be obtained by joining a tetrahedron to another Johnson solid, the tridiminished icosahedron.... |
 |
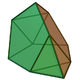 |
10 | 18 | 10 | 7 | 3 | C3v | ||||
| 65 | Augmented truncated tetrahedron Augmented truncated tetrahedron In geometry, the augmented truncated tetrahedron is one of the Johnson solids . It is created by attaching a triangular cupola to one hexagonal face of an truncated tetrahedron.-External links:**... |
 |
 |
15 | 27 | 14 | 8 | 3 | 3 | C3v | |||
| 66 | Augmented truncated cube Augmented truncated cube In geometry, the augmented truncated cube is one of theJohnson solids . As its name suggests, it is created by attaching square cupola onto one octagonal face of a truncated cube.-References:... |
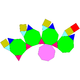 |
 |
28 | 48 | 22 | 12 | 5 | 5 | C4v | |||
| 67 | Biaugmented truncated cube Biaugmented truncated cube In geometry, the biaugmented truncated cube is one of the Johnson solids .-External links:**... |
 |
 |
32 | 60 | 30 | 16 | 10 | 4 | D4h | |||
| 68 | Augmented truncated dodecahedron Augmented truncated dodecahedron In geometry, the augmented truncated dodecahedron is one of the Johnson solids .-External links:**... |
 |
 |
65 | 105 | 42 | 25 | 5 | 1 | 11 | C5v | ||
| 69 | Parabiaugmented truncated dodecahedron Parabiaugmented truncated dodecahedron In geometry, the parabiaugmented truncated dodecahedron is one of the Johnson solids .-External links:**... |
 |
 |
70 | 120 | 52 | 30 | 10 | 2 | 10 | D5d | ||
| 70 | Metabiaugmented truncated dodecahedron Metabiaugmented truncated dodecahedron In geometry, the metabiaugmented truncated dodecahedron is one of the Johnson solids .-External links:**... |
 |
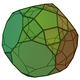 |
70 | 120 | 52 | 30 | 10 | 2 | 10 | C2v | ||
| 71 | Triaugmented truncated dodecahedron Triaugmented truncated dodecahedron In geometry, the triaugmented truncated dodecahedron is one of the Johnson solids ; of them, it has the greatest volume in proportion to side length.The 92 Johnson solids were named and described by Norman Johnson in 1966.-External links:**... |
 |
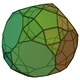 |
75 | 135 | 62 | 35 | 15 | 3 | 9 | C3v | ||
| 72 | Gyrate rhombicosidodecahedron Gyrate rhombicosidodecahedron In geometry, the gyrate rhombicosidodecahedron is one of theJohnson solids .The 92 Johnson solids were named and described by Norman Johnson in 1966.- Related polyhedron :... |
 |
 |
60 | 120 | 62 | 20 | 30 | 12 | C5v | |||
| 73 | Parabigyrate rhombicosidodecahedron Parabigyrate rhombicosidodecahedron In geometry, the parabigyrate rhombicosidodecahedron is one of the Johnson solids . It can be constructed as a rhombicosidodecahedron with two opposing pentagonal cupolae rotated through 36 degrees.... |
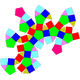 |
 |
60 | 120 | 62 | 20 | 30 | 12 | D5d | |||
| 74 | Metabigyrate rhombicosidodecahedron Metabigyrate rhombicosidodecahedron In geometry, the metabigyrate rhombicosidodecahedron is one of the Johnson solids . It can be constructed as a rhombicosidodecahedron with two non-opposing pentagonal cupolae rotated through 36 degrees.... |
 |
 |
60 | 120 | 62 | 20 | 30 | 12 | C2v | |||
| 75 | Trigyrate rhombicosidodecahedron Trigyrate rhombicosidodecahedron In geometry, the trigyrate rhombicosidodecahedron is one of theJohnson solids .It can be constructed as a rhombicosidodecahedron with three pentagonal cupolae rotated through 36 degrees.Related Johnson solids are... |
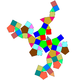 |
 |
60 | 120 | 62 | 20 | 30 | 12 | C3v | |||
| 76 | Diminished rhombicosidodecahedron Diminished rhombicosidodecahedron In geometry, the diminished rhombicosidodecahedron is one of theJohnson solids .It can be constructed as a rhombicosidodecahedron with one pentagonal cupola removed.The 92 Johnson solids were named and described by Norman Johnson in 1966.... |
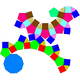 |
 |
55 | 105 | 52 | 15 | 25 | 11 | 1 | C5v | ||
| 77 | Paragyrate diminished rhombicosidodecahedron Paragyrate diminished rhombicosidodecahedron In geometry, the paragyrate diminished rhombicosidodecahedron is one of the Johnson solids .The 92 Johnson solids were named and described by Norman Johnson in 1966.-External links:**... |
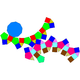 |
 |
55 | 105 | 52 | 15 | 25 | 11 | 1 | C5v | ||
| 78 | Metagyrate diminished rhombicosidodecahedron Metagyrate diminished rhombicosidodecahedron In geometry, the metagyrate diminished rhombicosidodecahedron is one of the Johnson solids .The 92 Johnson solids were named and described by Norman Johnson in 1966.-External links:**... |
 |
 |
55 | 105 | 52 | 15 | 25 | 11 | 1 | Cs | ||
| 79 | Bigyrate diminished rhombicosidodecahedron Bigyrate diminished rhombicosidodecahedron In geometry, the bigyrate diminished rhombicosidodecahedron is one of the Johnson solids .The 92 Johnson solids were named and described by Norman Johnson in 1966.-External links:**... |
 |
 |
55 | 105 | 52 | 15 | 25 | 11 | 1 | Cs | ||
| 80 | Parabidiminished rhombicosidodecahedron Parabidiminished rhombicosidodecahedron In geometry, the parabidiminished rhombicosidodecahedron is one of theJohnson solids .It can be constructed as a rhombicosidodecahedron with two opposing pentagonal cupola removed.Related Johnson solids are... |
 |
 |
50 | 90 | 42 | 10 | 20 | 10 | 2 | D5d | ||
| 81 | Metabidiminished rhombicosidodecahedron Metabidiminished rhombicosidodecahedron In geometry, the metabidiminished rhombicosidodecahedron is one of theJohnson solids .It can be constructed as a rhombicosidodecahedron with two non-opposing pentagonal cupolae removed.Related Johnson solids are... |
 |
 |
50 | 90 | 42 | 10 | 20 | 10 | 2 | C2v | ||
| 82 | Gyrate bidiminished rhombicosidodecahedron Gyrate bidiminished rhombicosidodecahedron In geometry, the gyrate bidiminished rhombicosidodecahedron is one of the Johnson solids .The 92 Johnson solids were named and described by Norman Johnson in 1966.-External links:**... |
 |
 |
50 | 90 | 42 | 10 | 20 | 10 | 2 | Cs | ||
| 83 | Tridiminished rhombicosidodecahedron Tridiminished rhombicosidodecahedron In geometry, the tridiminished rhombicosidodecahedron is one of theJohnson solids .It can be constructed as a rhombicosidodecahedron with three pentagonal cupola removed.Related Johnson solids are:... |
 |
 |
45 | 75 | 32 | 5 | 15 | 9 | 3 | C3v | ||
| 84 | Snub disphenoid Snub disphenoid In geometry, the snub disphenoid is one of the Johnson solids . It is a three-dimensional solid that has only equilateral triangles as faces, and is therefore a deltahedron. It is not a regular polyhedron because some vertices have four faces and others have five... (Siamese dodecahedron) |
 |
 |
8 | 18 | 12 | 12 | D2d | |||||
| 85 | Snub square antiprism Snub square antiprism In geometry, the snub square antiprism is one of theJohnson solids .It is one of the elementary Johnson solids that do not arise from "cut and paste" manipulations of the Platonic and Archimedean solids, although it is a relative of the Icosahedron that has fourfold symmetry instead of... |
 |
 |
16 | 40 | 26 | 24 | 2 | D4d | ||||
| 86 | Sphenocorona Sphenocorona In geometry, the sphenocorona is one of theJohnson solids .It is one of the elementary Johnson solids that do not arise from "cut and paste" manipulations of the Platonic and Archimedean solids.... |
 |
 |
10 | 22 | 14 | 12 | 2 | C2v | ||||
| 87 | Augmented sphenocorona Augmented sphenocorona In geometry, the augmented sphenocorona is one of theJohnson solids , and is obtained by addinga square pyramid to one of the square faces of the sphenocorona.... |
 |
 |
11 | 26 | 17 | 16 | 1 | Cs | ||||
| 88 | Sphenomegacorona Sphenomegacorona In geometry, the sphenomegacorona is one of theJohnson solids .It is one of the elementary Johnson solids that do not arise from "cut and paste" manipulations of the Platonic and Archimedean solids.... |
 |
 |
12 | 28 | 18 | 16 | 2 | C2v | ||||
| 89 | Hebesphenomegacorona Hebesphenomegacorona In geometry, the hebesphenomegacorona is one of theJohnson solids .It is one of the elementary Johnson solids that do not arise from "cut and paste" manipulations of the Platonic and Archimedean solids. It has 21 faces, 18 triangles and 3 squares, 33 edges, and 14 vertices.The 92 Johnson solids... |
 |
 |
14 | 33 | 21 | 18 | 3 | C2v | ||||
| 90 | Disphenocingulum Disphenocingulum In geometry, the disphenocingulum is one of theJohnson solids .It is one of the elementary Johnson solids that do not arise from "cut and paste" manipulations of the Platonic and Archimedean solids.... |
 |
 |
16 | 38 | 24 | 20 | 4 | D2d | ||||
| 91 | Bilunabirotunda Bilunabirotunda In geometry, the bilunabirotunda is one of the Johnson solids . It is one of the elementary Johnson solids that do not arise from "cut and paste" manipulations of the Platonic and Archimedean solids.... |
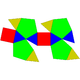 |
 |
14 | 26 | 14 | 8 | 2 | 4 | D2h | |||
| 92 | Triangular hebesphenorotunda Triangular hebesphenorotunda In geometry, the triangular hebesphenorotunda is one of the Johnson solids . It is one of the elementary Johnson solids, which do not arise from "cut and paste" manipulations of the Platonic and Archimedean solids. However, it does have a strong relationship to the icosidodecahedron, an Archimedean... |
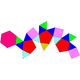 |
 |
18 | 36 | 20 | 13 | 3 | 3 | 1 | C3v |
Legend:
- Jn – Johnson Solid Number
- NetNet (polyhedron)In geometry the net of a polyhedron is an arrangement of edge-joined polygons in the plane which can be folded to become the faces of the polyhedron...
– Flattened (unfolded) image - V – Number of Vertices
- E – Number of Edges
- F – Number of Faces (total)
- F3 – Number of 3-sided Faces
- F4 – Number of 4-sided Faces
- F5 – Number of 5-sided Faces
- F6 – Number of 6-sided Faces
- F8 – Number of 8-sided Faces
- F10 – Number of 10-sided Faces
External links
- Sylvain Gagnon, "Convex polyhedra with regular faces", Structural Topology, No. 6, 1982, 83-95.
- Paper Models of Polyhedra Many links
- Johnson Solids by George W. Hart.
- Images of all 92 solids, categorized, on one page
- VRML models of Johnson Solids by Jim McNeill
- VRML models of Johnson Solids by Vladimir Bulatov

