
SO(4)
Encyclopedia
In mathematics
, the group
of rotations about a fixed point in four-dimensional Euclidean space
is denoted SO(4). The name comes from the fact that it is (isomorphic to) the special orthogonal group of order 4.
In this article rotation
means rotational displacement. For the sake of uniqueness rotation angles are assumed to be in the segment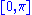 except where mentioned or clearly implied by the context otherwise.
except where mentioned or clearly implied by the context otherwise.
 .
.
Half-lines from O in the axis-plane A are not displaced; half-lines from O orthogonal to A are displaced through ; all other half-lines are displaced through an angle
; all other half-lines are displaced through an angle 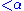 .
.
as a whole, i.e. rotated in themselves.
In general the rotation angles in plane A and
in plane A and 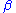 in plane B are different.
in plane B are different.
In that case A and B are the only pair of invariant planes, and half-lines from O in A, B are displaced through ,
, 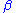 , and half-lines from O not in A or B are displaced through angles strictly between
, and half-lines from O not in A or B are displaced through angles strictly between  and
and 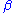 .
.
planes instead of just two, and all half-lines from O are displaced through the same angle. Such rotations are called isoclinic or equiangular rotations, or Clifford displacements. Beware: not all planes through O are invariant under isoclinic rotations; only planes that are spanned by a half-line and the corresponding displaced half-line are invariant.
There are two kinds of isoclinic 4D rotations. To see this, consider an isoclinic rotation R, and take an ordered set OU, OX, OY, OZ of mutually perpendicular half-lines at O (denoted as OUXYZ) such that OU and OX span an invariant plane, and therefore OY and OZ also span an invariant plane.
Now assume that only the rotation angle is specified. Then there are in general four isoclinic rotations in planes OUX and OYZ with rotation angle
is specified. Then there are in general four isoclinic rotations in planes OUX and OYZ with rotation angle  , depending on the rotation senses in OUX and OYZ.
, depending on the rotation senses in OUX and OYZ.
We make the convention that the rotation senses from OU to OX and from OY to OZ are reckoned positive. Then we have the four rotations R1 =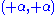 , R2 =
, R2 =  , R3 =
, R3 =  and R4 =
and R4 = 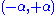 . R1 and R2 are each other's inverses
. R1 and R2 are each other's inverses
; so are R3 and R4.
Isoclinic rotations with like signs are denoted as left-isoclinic; those with opposite signs as right-isoclinic. Left- (Right-) isoclinic rotations are represented by left- (right-) multiplication by unit quaternions; see the paragraph "Relation to quaternions" below.
The four rotations are pairwise different except if or
or  .
.
 corresponds to the non-rotation;
corresponds to the non-rotation;  corresponds to the central inversion. These two elements of SO(4) are the only ones which are left- and right-isoclinic.
corresponds to the central inversion. These two elements of SO(4) are the only ones which are left- and right-isoclinic.
Left- and right-isocliny defined as above seem to depend on which specific isoclinic rotation was selected. However, when another isoclinic rotation R' with its own axes OU'X'Y'Z' is selected, then one can always choose the order of U', X', Y', Z' such that OUXYZ can be transformed into OU'X'Y'Z' by a rotation rather than by a rotation-reflection. Therefore, once one has selected a system OUXYZ of axes that is universally denoted as right-handed, one can determine the left or right character of a specific isoclinic rotation.
6-parameter
Lie group
.
Each plane through the rotation centre O is the axis-plane of a commutative subgroup
isomorphic to SO(2). All these subgroups are mutually conjugate
in SO(4).
Each pair of completely orthogonal planes through O is the pair of invariant
planes of a commutative subgroup of SO(4) isomorphic to SO(2) × SO(2).
These groups are maximal tori of SO(4), which are all mutually conjugate in SO(4). See also Clifford torus
.
All left-isoclinic rotations form a noncommutative subgroup S3L of SO(4) which is isomorphic to the multiplicative
group S3 of unit quaternions. All right-isoclinic rotations likewise form a subgroup S3R of SO(4) isomorphic to S3. Both S3L and S3R are maximal subgroups of SO(4).
Each left-isoclinic rotation commutes with each right-isoclinic rotation. This implies that there exists a direct product
S3L × S3R with normal subgroup
s S3L and S3R; both of the corresponding factor groups are isomorphic to the other factor of the direct product, i.e. isomorphic to S3.
Each 4D rotation R is in two ways the product of left- and right-isoclinic rotations RL and RR. RL and RR are together determined up to the central inversion, i.e. when both RL and RR are multiplied by the central inversion their product is R again.
This implies that S3L × S3R is the double cover of SO(4) and that S3L and S3R are normal subgroups of SO(4). The non-rotation I and the central inversion -I form a group C2 of order 2, which is the centre of SO(4) and of both S3L and S3R. The centre of a group is a normal subgroup of that group. The factor group of C2 in SO(4) is isomorphic to SO(3) × SO(3). The factor groups of C2 in S3L and S3R are isomorphic to SO(3).
The factor groups of S3L and S3R in SO(4) are isomorphic to SO(3).
s.
The even-dimensional rotation groups do contain the central inversion −I and have the group C2 = {I, −I} as their centre. From SO(6) onwards they are almost-simple in the sense that the factor groups of their centres are simple groups.
SO(4) is different: there is no conjugation
by any element of SO(4) that transforms left- and right-isoclinic rotations into each other. Reflection
s transform a left-isoclinic rotation into a right-isoclinic one by conjugation, and vice versa. This implies that under the group O(4) of all isometries with fixed point O the subgroups S3L and S3R are mutually conjugate and so are not normal subgroups of O(4). The 5D rotation group SO(5) and all higher rotation groups contain subgroups isomorphic to O(4). Like SO(4), all even-dimensional rotation groups contain isoclinic rotations. But unlike SO(4), in SO(6) and all higher even-dimensional rotation groups any pair of isoclinic rotations through the same angle is conjugate. The sets of all isoclinic rotations are not even subgroups of SO(2N), let alone normal subgroups.
linear
mappings of a 4D vector space
with inner product over the reals onto itself.
With respect to an orthonormal basis
in such a space SO(4) is represented as the group of real 4th-order orthogonal matrices with determinant
+1.
Let
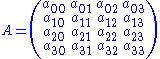
be its matrix with respect to an arbitrary orthonormal basis.
Calculate from this the so-called associate matrix
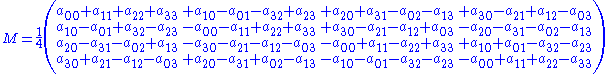
M has rank
one and is of unit Euclidean norm
as a 16D vector if and only if A is indeed a 4D rotation matrix. In this case there exist reals a, b, c, d; p, q, r, s such that
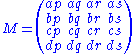
and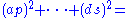
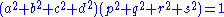 .
.
There are exactly two sets of a, b, c, d; p, q, r, s such that and
and 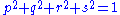 . They are each other's opposites.
. They are each other's opposites.
The rotation matrix then equals
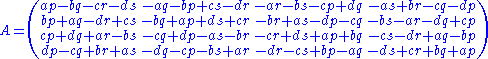
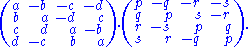
This formula is due to Van Elfrinkhof (1897).
The first factor in this decomposition represents a left-isoclinic rotation, the second factor a right-isoclinic rotation. The factors are determined up to the negative 4th-order identity matrix
, i.e. the central inversion.
u + xi + yj + zk.
A left-isoclinic rotation is represented by left-multiplication by a unit quaternion QL = a + bi + cj + dk. In matrix-vector language this is

Likewise, a right-isoclinic rotation is represented by right-multiplication by a unit quaternion QR = p + qi + rj + sk, which is in matrix-vector form
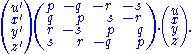
In the preceding section (Isoclinic decomposition) it is shown how a general 4D rotation is split into left- and right-isoclinic factors.
In quaternion language Van Elfrinkhof's formula reads
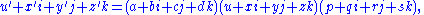
or in symbolic form
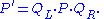
According to the German mathematician Felix Klein
this formula was already known to Cayley in 1854.
Quaternion multiplication is associative. Therefore
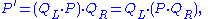
which shows that left-isoclinic and right-isoclinic rotations commute.
In quaternion notation, a rotation in SO(4) is a single rotation if and only if QL and QR are conjugate elements of the group of unit quaternions. This is equivalent to the statement that QL and QR have the same real part, i.e.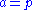 .
.
is identified with the subgroup of SO(4) consisting of the matrices
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of rotations about a fixed point in four-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
is denoted SO(4). The name comes from the fact that it is (isomorphic to) the special orthogonal group of order 4.
In this article rotation
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
means rotational displacement. For the sake of uniqueness rotation angles are assumed to be in the segment
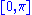 except where mentioned or clearly implied by the context otherwise.
except where mentioned or clearly implied by the context otherwise.Geometry of 4D rotations
There are two kinds of 4D rotations: simple rotations and double rotations.Simple rotations
A simple rotation R about a rotation centre O leaves an entire plane A through O (axis-plane) fixed. Every plane B that is completely orthogonal to A intersects A in a certain point P. Each such point P is the centre of the 2D rotation induced by R in B. All these 2D rotations have the same rotation angle .
.Half-lines from O in the axis-plane A are not displaced; half-lines from O orthogonal to A are displaced through
 ; all other half-lines are displaced through an angle
; all other half-lines are displaced through an angle 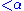 .
.Double rotations
A double rotation R about a rotation centre O leaves only O fixed. Any double rotation has at least one pair of completely orthogonal planes A and B through O that are invariantInvariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
as a whole, i.e. rotated in themselves.
In general the rotation angles
 in plane A and
in plane A and 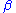 in plane B are different.
in plane B are different.In that case A and B are the only pair of invariant planes, and half-lines from O in A, B are displaced through
 ,
, 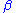 , and half-lines from O not in A or B are displaced through angles strictly between
, and half-lines from O not in A or B are displaced through angles strictly between  and
and 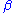 .
.Isoclinic rotations
If the rotation angles of a double rotation are equal then there are infinitely many invariantInvariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
planes instead of just two, and all half-lines from O are displaced through the same angle. Such rotations are called isoclinic or equiangular rotations, or Clifford displacements. Beware: not all planes through O are invariant under isoclinic rotations; only planes that are spanned by a half-line and the corresponding displaced half-line are invariant.
There are two kinds of isoclinic 4D rotations. To see this, consider an isoclinic rotation R, and take an ordered set OU, OX, OY, OZ of mutually perpendicular half-lines at O (denoted as OUXYZ) such that OU and OX span an invariant plane, and therefore OY and OZ also span an invariant plane.
Now assume that only the rotation angle
 is specified. Then there are in general four isoclinic rotations in planes OUX and OYZ with rotation angle
is specified. Then there are in general four isoclinic rotations in planes OUX and OYZ with rotation angle  , depending on the rotation senses in OUX and OYZ.
, depending on the rotation senses in OUX and OYZ.We make the convention that the rotation senses from OU to OX and from OY to OZ are reckoned positive. Then we have the four rotations R1 =
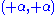 , R2 =
, R2 =  , R3 =
, R3 =  and R4 =
and R4 = 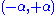 . R1 and R2 are each other's inverses
. R1 and R2 are each other's inversesInverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
; so are R3 and R4.
Isoclinic rotations with like signs are denoted as left-isoclinic; those with opposite signs as right-isoclinic. Left- (Right-) isoclinic rotations are represented by left- (right-) multiplication by unit quaternions; see the paragraph "Relation to quaternions" below.
The four rotations are pairwise different except if
 or
or  .
. corresponds to the non-rotation;
corresponds to the non-rotation;  corresponds to the central inversion. These two elements of SO(4) are the only ones which are left- and right-isoclinic.
corresponds to the central inversion. These two elements of SO(4) are the only ones which are left- and right-isoclinic.Left- and right-isocliny defined as above seem to depend on which specific isoclinic rotation was selected. However, when another isoclinic rotation R' with its own axes OU'X'Y'Z' is selected, then one can always choose the order of U', X', Y', Z' such that OUXYZ can be transformed into OU'X'Y'Z' by a rotation rather than by a rotation-reflection. Therefore, once one has selected a system OUXYZ of axes that is universally denoted as right-handed, one can determine the left or right character of a specific isoclinic rotation.
Group structure of SO(4)
SO(4) is a noncommutative compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
6-parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
.
Each plane through the rotation centre O is the axis-plane of a commutative subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
isomorphic to SO(2). All these subgroups are mutually conjugate
Conjugation of isometries in Euclidean space
In a group, the conjugate by g of h is ghg−1.-Translation:If h is a translation, then its conjugate by an isometry can be described as applying the isometry to the translation:...
in SO(4).
Each pair of completely orthogonal planes through O is the pair of invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
planes of a commutative subgroup of SO(4) isomorphic to SO(2) × SO(2).
These groups are maximal tori of SO(4), which are all mutually conjugate in SO(4). See also Clifford torus
Clifford torus
In geometric topology, the Clifford torus is a special kind of torus sitting inside R4. Alternatively, it can be seen as a torus sitting inside C2 since C2 is topologically the same space as R4...
.
All left-isoclinic rotations form a noncommutative subgroup S3L of SO(4) which is isomorphic to the multiplicative
Multiplicative
Multiplicative may refer to:*Multiplication*Multiplicative partition*A Multiplicative function* For the Multiplicative numerals, once, twice, and thrice, see English numerals...
group S3 of unit quaternions. All right-isoclinic rotations likewise form a subgroup S3R of SO(4) isomorphic to S3. Both S3L and S3R are maximal subgroups of SO(4).
Each left-isoclinic rotation commutes with each right-isoclinic rotation. This implies that there exists a direct product
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
S3L × S3R with normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
s S3L and S3R; both of the corresponding factor groups are isomorphic to the other factor of the direct product, i.e. isomorphic to S3.
Each 4D rotation R is in two ways the product of left- and right-isoclinic rotations RL and RR. RL and RR are together determined up to the central inversion, i.e. when both RL and RR are multiplied by the central inversion their product is R again.
This implies that S3L × S3R is the double cover of SO(4) and that S3L and S3R are normal subgroups of SO(4). The non-rotation I and the central inversion -I form a group C2 of order 2, which is the centre of SO(4) and of both S3L and S3R. The centre of a group is a normal subgroup of that group. The factor group of C2 in SO(4) is isomorphic to SO(3) × SO(3). The factor groups of C2 in S3L and S3R are isomorphic to SO(3).
The factor groups of S3L and S3R in SO(4) are isomorphic to SO(3).
Special property of SO(4) among rotation groups in general
The odd-dimensional rotation groups do not contain the central inversion and are simple groupSimple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
s.
The even-dimensional rotation groups do contain the central inversion −I and have the group C2 = {I, −I} as their centre. From SO(6) onwards they are almost-simple in the sense that the factor groups of their centres are simple groups.
SO(4) is different: there is no conjugation
Conjugation of isometries in Euclidean space
In a group, the conjugate by g of h is ghg−1.-Translation:If h is a translation, then its conjugate by an isometry can be described as applying the isometry to the translation:...
by any element of SO(4) that transforms left- and right-isoclinic rotations into each other. Reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
s transform a left-isoclinic rotation into a right-isoclinic one by conjugation, and vice versa. This implies that under the group O(4) of all isometries with fixed point O the subgroups S3L and S3R are mutually conjugate and so are not normal subgroups of O(4). The 5D rotation group SO(5) and all higher rotation groups contain subgroups isomorphic to O(4). Like SO(4), all even-dimensional rotation groups contain isoclinic rotations. But unlike SO(4), in SO(6) and all higher even-dimensional rotation groups any pair of isoclinic rotations through the same angle is conjugate. The sets of all isoclinic rotations are not even subgroups of SO(2N), let alone normal subgroups.
Algebra of 4D rotations
SO(4) is commonly identified with the group of orientation-preserving isometricIsometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
mappings of a 4D vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
with inner product over the reals onto itself.
With respect to an orthonormal basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
in such a space SO(4) is represented as the group of real 4th-order orthogonal matrices with determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
+1.
Isoclinic decomposition
A 4D rotation given by its matrix is decomposed into a left-isoclinic and a right-isoclinic rotation as follows:Let
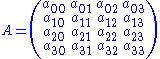
be its matrix with respect to an arbitrary orthonormal basis.
Calculate from this the so-called associate matrix
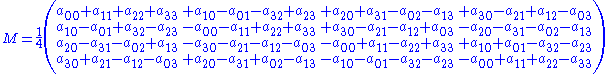
M has rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
one and is of unit Euclidean norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
as a 16D vector if and only if A is indeed a 4D rotation matrix. In this case there exist reals a, b, c, d; p, q, r, s such that
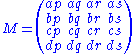
and
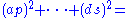
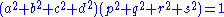 .
.There are exactly two sets of a, b, c, d; p, q, r, s such that
 and
and 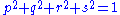 . They are each other's opposites.
. They are each other's opposites.The rotation matrix then equals
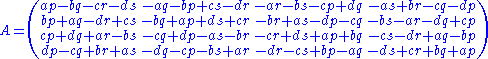
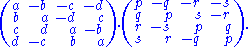
This formula is due to Van Elfrinkhof (1897).
The first factor in this decomposition represents a left-isoclinic rotation, the second factor a right-isoclinic rotation. The factors are determined up to the negative 4th-order identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
, i.e. the central inversion.
Relation to quaternions
A point in 4D space with Cartesian coordinates (u, x, y, z) may be represented by a quaternionQuaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
u + xi + yj + zk.
A left-isoclinic rotation is represented by left-multiplication by a unit quaternion QL = a + bi + cj + dk. In matrix-vector language this is

Likewise, a right-isoclinic rotation is represented by right-multiplication by a unit quaternion QR = p + qi + rj + sk, which is in matrix-vector form
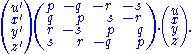
In the preceding section (Isoclinic decomposition) it is shown how a general 4D rotation is split into left- and right-isoclinic factors.
In quaternion language Van Elfrinkhof's formula reads
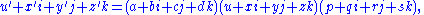
or in symbolic form
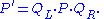
According to the German mathematician Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
this formula was already known to Cayley in 1854.
Quaternion multiplication is associative. Therefore
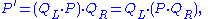
which shows that left-isoclinic and right-isoclinic rotations commute.
In quaternion notation, a rotation in SO(4) is a single rotation if and only if QL and QR are conjugate elements of the group of unit quaternions. This is equivalent to the statement that QL and QR have the same real part, i.e.
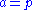 .
.The Euler–Rodrigues formula for 3D rotations
Our ordinary 3D space is conveniently treated as the subspace with coordinate system OXYZ of the 4D space with coordinate system OUXYZ. Its rotation groupRotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
is identified with the subgroup of SO(4) consisting of the matrices
-

In Van Elfrinkhof's formula in the preceding subsection this restriction to three dimensions leads to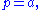
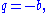
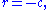
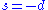 , or in quaternion representation: QR = QL
, or in quaternion representation: QR = QL' = QL−1.
The 3D rotation matrix then becomes
-

which is the representation of the 3D rotation by its Euler–Rodrigues parameters.
The corresponding quaternion formula
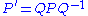 , (
, (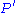 is / means P - prime)
is / means P - prime)
where Q = QL, or, in expanded form:
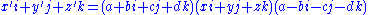
is known as the HamiltonWilliam Rowan HamiltonSir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
–CayleyArthur CayleyArthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....
formula.
See also
- orthogonal matrixOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
- orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
- rotation groupRotation groupIn mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
- Lorentz groupLorentz groupIn physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
- Poincaré groupPoincaré groupIn physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
- Laplace–Runge–Lenz vector
- Plane of rotationPlane of rotationIn geometry, a plane of rotation is an abstract object used to describe or visualise rotations in space. In three dimensions it is an alternative to the axis of rotation, but unlike the axis of rotation it can be used in other dimensions, such as two, four or more dimensions.Mathematically such...
- orthogonal matrix
-

