Spherical 3-manifold
Encyclopedia
In mathematics
, a spherical 3-manifold M is a 3-manifold
of the form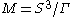
where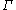
is a finite
subgroup
of SO(4) acting freely
by rotations on the 3-sphere
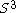. All such manifolds are prime
, orientable, and closed
. Spherical 3-manifolds are sometimes called elliptic 3-manifolds or Clifford-Klein manifolds.
isomorphic to Γ itself. The elliptization conjecture
, proved by Grigori Perelman
, states that conversely all 3-manifolds with finite fundamental group are spherical manifolds.
The fundamental group is either cyclic
, or is a central extension of a dihedral
, tetrahedral, octahedral, or icosahedral group by a cyclic group of even order. This divides the set of such manifolds into 5 classes, described in the following sections.
The spherical manifolds are exactly the manifolds with spherical geometry, one of the 8 geometries of Thurston's geometrization conjecture
.
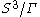with Γ cyclic
are precisely the 3-dimensional lens space
s. A lens space is not determined by its fundamental group (there are non-homeomorphic lens spaces with isomorphic fundamental groups); but any other spherical manifold is.
Three-dimensional lens spaces arise as quotients of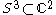
by
the action of the group that is generated by elements of the form
where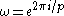
. Such a lens space 
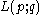has fundamental group 
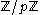for all 
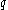, so spaces with different 
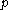are not homotopy equivalent.
Moreover, classifications up to homeomorphism and homotopy equivalence are known, as follows. The three-dimensional spaces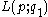
and
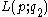are:
In particular, the lens spaces L(7,1) and L(7,2) give examples of two 3-manifolds that are homotopy equivalent but not homeomorphic.
The lens space L(1,0) is the 3-sphere, and the lens space L(2,1) is 3 dimensional real projective space.
Lens spaces can be represented as Seifert fiber space
s in many ways, usually as fiber spaces over the 2-sphere with at most two exceptional fibers, though the lens space with fundamental group of order 4 also has a representation as a Seifert fiber space over the projective plane with no exceptional fibers.
M whose fundamental group
is a central extension of a dihedral group.
The fundamental group π1(M) of M is given by the presentation
for integers m, n with m ≥ 1, n ≥ 2.
This group is a metacyclic group
of order 4mn with abelianization of order 4m (so m and n are both determined by this group).
The element y generates a cyclic
normal subgroup
of order 2n, and the element x has order 4m. The center
is cyclic of order 2m and is generated by x2, and the quotient by the center is the dihedral group
of order 2n.
The simplest example is m = 1, n = 2, when π1(M) is the quaternion group
of order 8.
Prism manifolds are uniquely determined by their fundamental groups: if a closed 3-manifold has the same fundamental group as a prism manifold M, it is homeomorphic
to M.
Prism manifolds can be represented as Seifert fiber space
s in two ways.
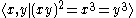
or a group of order 8×3k, k ≥ 1 with presentation
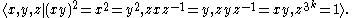
These manifolds are uniquely determined by their fundamental groups. They can all be represented in an essentially unique way as Seifert fiber space
s: the quotient manifold is a sphere and there are 3 exceptional fibers of orders 2, 3, and 3.
These manifolds are uniquely determined by their fundamental groups. They can all be represented in an essentially unique way as Seifert fiber space
s: the quotient manifold is a sphere and there are 3 exceptional fibers of orders 2, 3, and 4.
When m is 1, the manifold is the Poincaré homology sphere.
These manifolds are uniquely determined by their fundamental groups. They can all be represented in an essentially unique way as Seifert fiber spaces: the quotient manifold is a sphere and there are 3 exceptional fibers of orders 2, 3, and 5.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a spherical 3-manifold M is a 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
of the form
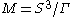
where
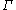is a finiteFinite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of SO(4) acting freely
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
by rotations on the 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
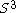. All such manifolds are primePrime decomposition (3-manifold)
In mathematics, the prime decomposition theorem for 3-manifolds states that every compact, orientable 3-manifold is the connected sum of a unique collection of prime 3-manifolds....
, orientable, and closed
Closed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
. Spherical 3-manifolds are sometimes called elliptic 3-manifolds or Clifford-Klein manifolds.
Properties
A spherical 3-manifold has a finite fundamental groupFundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
isomorphic to Γ itself. The elliptization conjecture
Thurston elliptization conjecture
William Thurston's elliptization conjecture states that a closed 3-manifold with finite fundamental group is spherical, i.e. has a Riemannian metric of constant positive sectional curvature. A 3-manifold with such a metric is covered by the 3-sphere, moreover the group of covering transformations...
, proved by Grigori Perelman
Grigori Perelman
Grigori Yakovlevich Perelman is a Russian mathematician who has made landmark contributions to Riemannian geometry and geometric topology.In 1992, Perelman proved the soul conjecture. In 2002, he proved Thurston's geometrization conjecture...
, states that conversely all 3-manifolds with finite fundamental group are spherical manifolds.
The fundamental group is either cyclic
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
, or is a central extension of a dihedral
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
, tetrahedral, octahedral, or icosahedral group by a cyclic group of even order. This divides the set of such manifolds into 5 classes, described in the following sections.
The spherical manifolds are exactly the manifolds with spherical geometry, one of the 8 geometries of Thurston's geometrization conjecture
Geometrization conjecture
Thurston's geometrization conjecture states that compact 3-manifolds can be decomposed canonically into submanifolds that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem for surfaces...
.
Cyclic case (lens spaces)
The manifolds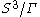 with Γ cyclicCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
are precisely the 3-dimensional lens space
Lens space
A lens space is an example of a topological space, considered in mathematics. The term often refers to a specific class of 3-manifolds, but in general can be defined for higher dimensions....
s. A lens space is not determined by its fundamental group (there are non-homeomorphic lens spaces with isomorphic fundamental groups); but any other spherical manifold is.
Three-dimensional lens spaces arise as quotients of
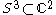bythe action of the group that is generated by elements of the form
where
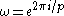. Such a lens space 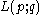has fundamental group 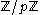for all 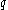, so spaces with different 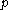are not homotopy equivalent.Moreover, classifications up to homeomorphism and homotopy equivalence are known, as follows. The three-dimensional spaces
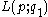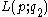and are:
- homotopy equivalent if and only if
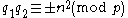for some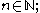 
- homeomorphic if and only if
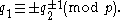
In particular, the lens spaces L(7,1) and L(7,2) give examples of two 3-manifolds that are homotopy equivalent but not homeomorphic.
The lens space L(1,0) is the 3-sphere, and the lens space L(2,1) is 3 dimensional real projective space.
Lens spaces can be represented as Seifert fiber space
Seifert fiber space
A Seifert fiber space is a 3-manifold together with a "nice" decomposition as a disjoint union of circles. In other words it is a S^1-bundle over a 2-dimensional orbifold...
s in many ways, usually as fiber spaces over the 2-sphere with at most two exceptional fibers, though the lens space with fundamental group of order 4 also has a representation as a Seifert fiber space over the projective plane with no exceptional fibers.
Dihedral case (prism manifolds)
A prism manifold is a closed 3-dimensional manifold3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
M whose fundamental group
is a central extension of a dihedral group.
The fundamental group π1(M) of M is given by the presentation
for integers m, n with m ≥ 1, n ≥ 2.
This group is a metacyclic group
Metacyclic group
In group theory, a metacyclic group is an extension of a cyclic group by a cyclic group. That is, it is a group G for which there is a short exact sequence1 \rightarrow K \rightarrow G \rightarrow H \rightarrow 1,\,where H and K are cyclic...
of order 4mn with abelianization of order 4m (so m and n are both determined by this group).
The element y generates a cyclic
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of order 2n, and the element x has order 4m. The center
Center (group theory)
In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
is cyclic of order 2m and is generated by x2, and the quotient by the center is the dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
of order 2n.
The simplest example is m = 1, n = 2, when π1(M) is the quaternion group
Quaternion group
In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
of order 8.
Prism manifolds are uniquely determined by their fundamental groups: if a closed 3-manifold has the same fundamental group as a prism manifold M, it is homeomorphic
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to M.
Prism manifolds can be represented as Seifert fiber space
Seifert fiber space
A Seifert fiber space is a 3-manifold together with a "nice" decomposition as a disjoint union of circles. In other words it is a S^1-bundle over a 2-dimensional orbifold...
s in two ways.
Tetrahedral case
The fundamental group is a product of a cyclic group of order m coprime to 6 with the binary tetrahedral group (of order 24) which has the presentation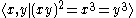or a group of order 8×3k, k ≥ 1 with presentation
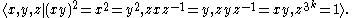
These manifolds are uniquely determined by their fundamental groups. They can all be represented in an essentially unique way as Seifert fiber space
Seifert fiber space
A Seifert fiber space is a 3-manifold together with a "nice" decomposition as a disjoint union of circles. In other words it is a S^1-bundle over a 2-dimensional orbifold...
s: the quotient manifold is a sphere and there are 3 exceptional fibers of orders 2, 3, and 3.
Octahedral case
The fundamental group is a product of a cyclic group of order m coprime to 6 with the binary octahedral group (of order 48) which has the presentationThese manifolds are uniquely determined by their fundamental groups. They can all be represented in an essentially unique way as Seifert fiber space
Seifert fiber space
A Seifert fiber space is a 3-manifold together with a "nice" decomposition as a disjoint union of circles. In other words it is a S^1-bundle over a 2-dimensional orbifold...
s: the quotient manifold is a sphere and there are 3 exceptional fibers of orders 2, 3, and 4.
Icosahedral case
The fundamental group is a product of a cyclic group of order m coprime to 30 with the binary icosahedral group (order 120) which has the presentationWhen m is 1, the manifold is the Poincaré homology sphere.
These manifolds are uniquely determined by their fundamental groups. They can all be represented in an essentially unique way as Seifert fiber spaces: the quotient manifold is a sphere and there are 3 exceptional fibers of orders 2, 3, and 5.