
600-cell
Encyclopedia
In geometry
, the 600-cell (or hexacosichoron) is the convex regular 4-polytope
, or polychoron
, with Schläfli symbol {3,3,5}. Its boundary is composed of 600 tetrahedral
cells with 20 meeting at each vertex. Together they form 1200 triangular faces, 720 edges, and 120 vertices. The edges form 72 flat regular decagons. Each vertex of the 600-cell is a vertex of six such decagons.
The mutual distances of the vertices, measured in degrees of arc on the circumscribed hypersphere
, only have the values 36° = , 60°=
, 60°=  , 72° =
, 72° =  , 90° =
, 90° =  , 108° =
, 108° =  , 120° =
, 120° =  , 144° =
, 144° =  , and 180° =
, and 180° =  . Departing from an arbitrary vertex V one has at 36° and 144° the 12 vertices of an icosahedron
. Departing from an arbitrary vertex V one has at 36° and 144° the 12 vertices of an icosahedron
, at 60° and 120° the 20 vertices of a dodecahedron, at 72° and 108° again the 12 vertices of an icosahedron, at 90° the 30 vertices of an icosadodecahedron, and finally at 180° the antipodal vertex of V. References: S.L. van Oss (1899); F. Buekenhout and M. Parker (1998).
The 600-cell is regarded as the 4-dimensional analog of the icosahedron
, since it has five tetrahedra
meeting at every edge, just as the icosahedron has five triangle
s meeting at every vertex. It is also called a tetraplex (abbreviated from "tetrahedral complex") and polytetrahedron
, being bounded by tetrahedral cells
.
Its vertex figure
is an icosahedron
, and its dual polytope is the 120-cell.
Each cell touches, in some manner, 56 other cells. One cell contacts each of the four faces; two cells contact each of the six edges, but not a face; and ten cells contact each of the four vertices, but not a face or edge.
), can be given as follows: 16 vertices of the form:
,
and 8 vertices obtained from
by permuting coordinates. The remaining 96 vertices are obtained by taking even permutations of
Note that the first 16 vertices are the vertices of a tesseract
, the second eight are the vertices of a 16-cell
, and that all 24 vertices together are vertices of a 24-cell. The final 96 vertices are the vertices of a snub 24-cell
, which can be found by partitioning each of the 96 edges of another 24-cell (dual to the first) in the golden ratio in a consistent manner.
When interpreted as quaternion
s, the 120 vertices of the 600-cell form a group
under quaternionic multiplication. This group is often called the binary icosahedral group and denoted by 2I as it is the double cover of the ordinary icosahedral group I. It occurs twice in the rotational symmetry group RSG of the 600-cell as an invariant subgroup, namely as the subgroup 2IL of quaternion left-multiplications and as the subgroup 2IR of quaternion right-multiplications. Each rotational symmetry of the 600-cell is generated by specific elements of 2IL and 2IR; the pair of opposite elements generate the same element of RSG. The centre of RSG consists of the non-rotation Id and the central inversion -Id. We have the isomorphism RSG ≅ (2IL × 2IR) / {Id, -Id}. The order of RSG equals 120 × 120 / 2 = 7200.
The binary icosahedral group is isomorphic to SL(2,5)
.
The full symmetry group
of the 600-cell is the Weyl group
of H4. This is a group
of order 14400. It consists of 7200 rotations
and 7200 rotation-reflections. The rotations form an invariant subgroup of the full symmetry group. The rotational symmetry group was described by S.L. van Oss (1899); see References.
Frame synchronized animated comparison of the 600 cell using orthogonal isometric (left) and perspective (right) projections.
may be obtained from the 600-cell by removing the vertices of an inscribed 24-cell and taking the convex hull
of the remaining vertices. This process is a diminishing of the 600-cell.
The grand antiprism
may be obtained by another diminishing of the 600-cell: removing 20 vertices that lie on two mutually orthogonal rings and taking the convex hull of the remaining vertices.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the 600-cell (or hexacosichoron) is the convex regular 4-polytope
Convex regular 4-polytope
In mathematics, a convex regular 4-polytope is a 4-dimensional polytope that is both regular and convex. These are the four-dimensional analogs of the Platonic solids and the regular polygons ....
, or polychoron
Polychoron
In geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...
, with Schläfli symbol {3,3,5}. Its boundary is composed of 600 tetrahedral
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
cells with 20 meeting at each vertex. Together they form 1200 triangular faces, 720 edges, and 120 vertices. The edges form 72 flat regular decagons. Each vertex of the 600-cell is a vertex of six such decagons.
The mutual distances of the vertices, measured in degrees of arc on the circumscribed hypersphere
Hypersphere
In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...
, only have the values 36° =
 , 60°=
, 60°=  , 72° =
, 72° =  , 90° =
, 90° =  , 108° =
, 108° =  , 120° =
, 120° =  , 144° =
, 144° =  , and 180° =
, and 180° =  . Departing from an arbitrary vertex V one has at 36° and 144° the 12 vertices of an icosahedron
. Departing from an arbitrary vertex V one has at 36° and 144° the 12 vertices of an icosahedronIcosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
, at 60° and 120° the 20 vertices of a dodecahedron, at 72° and 108° again the 12 vertices of an icosahedron, at 90° the 30 vertices of an icosadodecahedron, and finally at 180° the antipodal vertex of V. References: S.L. van Oss (1899); F. Buekenhout and M. Parker (1998).
The 600-cell is regarded as the 4-dimensional analog of the icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
, since it has five tetrahedra
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
meeting at every edge, just as the icosahedron has five triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s meeting at every vertex. It is also called a tetraplex (abbreviated from "tetrahedral complex") and polytetrahedron
Polytetrahedron
Polytetrahedron is a term used for three distinct types of objects, all basedon the tetrahedron:*A uniform convex polychoron made up of 600 tetrahedral cells. It is more commonly known as a 600-cell or hexacosichoron...
, being bounded by tetrahedral cells
Cell (geometry)
In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made...
.
Its vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
is an icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
, and its dual polytope is the 120-cell.
Each cell touches, in some manner, 56 other cells. One cell contacts each of the four faces; two cells contact each of the six edges, but not a face; and ten cells contact each of the four vertices, but not a face or edge.
Coordinates
The vertices of a 600-cell centered at the origin of 4-space, with edges of length 1/φ (where φ = (1+√5)/2 is the golden ratioGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
), can be given as follows: 16 vertices of the form:
,
and 8 vertices obtained from
by permuting coordinates. The remaining 96 vertices are obtained by taking even permutations of
- ½(±1,±φ,±1/φ,0).
Note that the first 16 vertices are the vertices of a tesseract
Tesseract
In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...
, the second eight are the vertices of a 16-cell
16-cell
In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....
, and that all 24 vertices together are vertices of a 24-cell. The final 96 vertices are the vertices of a snub 24-cell
Snub 24-cell
In geometry, the snub 24-cell is a convex uniform polychoron composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices....
, which can be found by partitioning each of the 96 edges of another 24-cell (dual to the first) in the golden ratio in a consistent manner.
When interpreted as quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s, the 120 vertices of the 600-cell form a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under quaternionic multiplication. This group is often called the binary icosahedral group and denoted by 2I as it is the double cover of the ordinary icosahedral group I. It occurs twice in the rotational symmetry group RSG of the 600-cell as an invariant subgroup, namely as the subgroup 2IL of quaternion left-multiplications and as the subgroup 2IR of quaternion right-multiplications. Each rotational symmetry of the 600-cell is generated by specific elements of 2IL and 2IR; the pair of opposite elements generate the same element of RSG. The centre of RSG consists of the non-rotation Id and the central inversion -Id. We have the isomorphism RSG ≅ (2IL × 2IR) / {Id, -Id}. The order of RSG equals 120 × 120 / 2 = 7200.
The binary icosahedral group is isomorphic to SL(2,5)
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
.
The full symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of the 600-cell is the Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of H4. This is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of order 14400. It consists of 7200 rotations
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
and 7200 rotation-reflections. The rotations form an invariant subgroup of the full symmetry group. The rotational symmetry group was described by S.L. van Oss (1899); see References.
Visualization
The symmetries of the 3-D surface of the 600-cell are somewhat difficult to visualize due to both the large number of tetrahedral cells, and the fact that the tetrahedron has no opposing faces or vertices. One can start by realizing the 600-cell is the dual of the 120-cell.Union of two tori
The 120-cell can be decomposed into two disjoint tori. Since it is the dual of the 600-cell, this same dual tori structure exists in the 600-cell, although it is somewhat more complex. The 10-cell geodesic path in the 120-cell corresponds to a 10-vertex decagon path in the 600-cell. Start by assembling five tetrahedrons around a common edge. This structure looks somewhat like an angular "flying saucer". Stack ten of these, vertex to vertex, "pancake" style. Fill in the annular ring between each "saucer" with 10 tetrahedrons forming an icosahedron. You can view this as five, vertex stacked, icosahedra, with the five extra annular ring gaps also filled in. You now have a torus consisting of 150 cells, ten edges long, with 100 exposed triangular faces. Stack another tetrahedron on each exposed face. This will give you a somewhat spiny torus of 250 cells with 50 raised vertices and 100 valley edges. Build a second identical torus of 250 cells that interlinks with the first. This accounts for 500 cells. These two tori mate together, leaving 100 tetrahedral voids that are filled with the remaining 100 tetrahedra.2D projections
| H4 | - | F4 |
|---|---|---|
[30] |
[20] |
[12] |
| H3 | A2 / B3 / D4 | A3 / B2 |
[10] |
[6] |
[4] |
3D projections
| Vertex-first projection | |
|---|---|
 |
This image shows a vertex-first perspective projection of the 600-cell into 3D. The 600-cell is scaled to a vertex-center radius of 1, and the 4D viewpoint is placed 5 units away. Then the following enhancements are applied:
|
| Cell-first projection | |
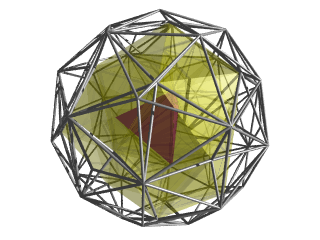 |
This image shows the 600-cell in cell-first perspective projection into 3D. Again, the 600-cell to a vertex-center radius of 1 and the 4D viewpoint is placed 5 units away. The following enhancements are then applied:
This particular viewpoint shows a nice outline of 5 tetrahedra sharing an edge, towards the front of the 3D image. |
| Stereographic projection (on 3-sphere 3-sphere In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space... ) |
|
 |
Cell-Centered |
| Simple Rotation | |
| A 3D projection of a 600-cell performing a simple rotation. | |
Frame synchronized animated comparison of the 600 cell using orthogonal isometric (left) and perspective (right) projections.
Related polychora
The snub 24-cellSnub 24-cell
In geometry, the snub 24-cell is a convex uniform polychoron composed of 120 regular tetrahedral and 24 icosahedral cells. Five tetrahedra and three icosahedra meet at each vertex. In total it has 480 triangular faces, 432 edges, and 96 vertices....
may be obtained from the 600-cell by removing the vertices of an inscribed 24-cell and taking the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of the remaining vertices. This process is a diminishing of the 600-cell.
The grand antiprism
Grand antiprism
In geometry, the grand antiprism or pentagonal double antiprismoid is a uniform polychoron bounded by 320 cells: 20 pentagonal antiprisms, and 300 tetrahedra. It is an anomalous, non-Wythoffian uniform polychoron, discovered in 1965 by Conway and Guy.- Alternate names :* Pentagonal double...
may be obtained by another diminishing of the 600-cell: removing 20 vertices that lie on two mutually orthogonal rings and taking the convex hull of the remaining vertices.
External links
-
- Der 600-Zeller (600-cell) Marco Möller's Regular polytopes in R4 (German)
- The 600-Cell Vertex centered expansion of the 600-cell

