120-cell
Encyclopedia
In geometry
, the 120-cell (or hecatonicosachoron) is the convex regular 4-polytope
with Schläfli symbol {5,3,3}.
The boundary of the 120-cell is composed of 120 dodecahedral cells with 4 meeting at each vertex.
It can be thought of as the 4-dimensional analog of the dodecahedron and has been called a dodecaplex (short for "dodecahedral complex"), hyperdodecahedron, and polydodecahedron. Just as a dodecahedron can be built up as a model with 12 pentagons, 3 around each vertex, the dodecaplex can be built up from 120 dodecahedrons, with 3 around each edge.
The Davis 120-cell, introduced by , is a compact 4-dimensional hyperbolic manifold
obtained by identifying opposite faces of the 120-cell, whose universal cover gives the regular honeycomb {5,3,3,5} of 4-dimensional hyperbolic space.
s of:
and all even permutations of
where φ (also called τ) is the golden ratio
, (1+√5)/2.
and the 24-cell). One can stack dodecahedrons face to face in a straight line bent in the 4th direction into a great circle with a circumference of 10 cells. Starting from this initial ten cell construct there are two common visualizations one can use: a layered stereographic projection, and a structure of intertwining rings.
Starting at the North Pole, we can build up the 120-cell in 9 latitudinal layers, with allusions to terrestrial 2-sphere topography in the table below. With the exception of the poles, each layer represents a separate 2-sphere, with the equator being a great 2-sphere. The centroids of the 30 equatorial cells form the vertices of an icosidodecahedron
, with the meridians (as described above) passing through the center of each pentagonal face. The cells labeled "interstitial" in the following table do not fall on meridian great circles.
Layers 3 and 7's cells are located directly over the pole cell's vertices. Layer 5's cells are located over the pole cell's edges.
) tori. If the center ring of the first torus is a meridian great circle as defined above, the center ring of the second torus is the equatorial great circle that is centered on the meridian circle.
Also note that the spiraling shell of 50 cells around a center ring can be either left handed or right handed. It's just a matter of partitioning the cells in the shell differently, i.e. picking another set of disjoint great circles.
3-dimensional orthogonal projections can also be made with three orthonormal basis vectors, and displayed as a 3d model, and then projecting a certain perspective in 3D for a 2d image.
use the same approach, but are shown with curved edges, representing the polytope a tiling of a 3-sphere
.
A comparison of perspective projections from 3D to 2D is shown in anology.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the 120-cell (or hecatonicosachoron) is the convex regular 4-polytope
Convex regular 4-polytope
In mathematics, a convex regular 4-polytope is a 4-dimensional polytope that is both regular and convex. These are the four-dimensional analogs of the Platonic solids and the regular polygons ....
with Schläfli symbol {5,3,3}.
The boundary of the 120-cell is composed of 120 dodecahedral cells with 4 meeting at each vertex.
It can be thought of as the 4-dimensional analog of the dodecahedron and has been called a dodecaplex (short for "dodecahedral complex"), hyperdodecahedron, and polydodecahedron. Just as a dodecahedron can be built up as a model with 12 pentagons, 3 around each vertex, the dodecaplex can be built up from 120 dodecahedrons, with 3 around each edge.
The Davis 120-cell, introduced by , is a compact 4-dimensional hyperbolic manifold
Hyperbolic manifold
In mathematics, a hyperbolic n-manifold is a complete Riemannian n-manifold of constant sectional curvature -1.Every complete, connected, simply-connected manifold of constant negative curvature −1 is isometric to the real hyperbolic space Hn. As a result, the universal cover of any closed manifold...
obtained by identifying opposite faces of the 120-cell, whose universal cover gives the regular honeycomb {5,3,3,5} of 4-dimensional hyperbolic space.
Elements
- There are 120 cells, 720 pentagonPentagonIn geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
al faces, 1200 edges, and 600 vertices. - There are 4 dodecahedra, 6 pentagons, and 4 edges meeting at every vertex.
- There are 3 dodecahedra and 3 pentagons meeting every edge.
- The dual polytope of the 120-cell is the 600-cell.
- The vertex figureVertex figureIn geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
of the 120-cell is a tetrahedronTetrahedronIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
.
Cartesian coordinates
The 600 vertices of the 120-cell include all permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s of:
- (0, 0, ±2, ±2)
- (±1, ±1, ±1, ±√5)
- (±φ-2, ±φ, ±φ, ±φ)
- (±φ-1, ±φ-1, ±φ-1, ±φ2)
and all even permutations of
- (0, ±φ-2, ±1, ±φ2)
- (0, ±φ-1, ±φ, ±√5)
- (±φ-1, ±1, ±φ, ±2)
where φ (also called τ) is the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
, (1+√5)/2.
Visualization
The 120-cell consists of 120 dodecahedral cells. For visualization purposes, it is convenient that the dodecahedron has opposing parallel faces (a trait it shares with the cells of the tesseractTesseract
In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...
and the 24-cell). One can stack dodecahedrons face to face in a straight line bent in the 4th direction into a great circle with a circumference of 10 cells. Starting from this initial ten cell construct there are two common visualizations one can use: a layered stereographic projection, and a structure of intertwining rings.
Layered stereographic projection
The cell locations lend themselves to a hyperspherical description. Pick an arbitrary cell and label it the "North Pole". Twelve great circle meridians (four cells long) radiate out in 3 dimensions, converging at the 5th "South Pole" cell. This skeleton accounts for 50 of the 120 cells (2 + 4*12).Starting at the North Pole, we can build up the 120-cell in 9 latitudinal layers, with allusions to terrestrial 2-sphere topography in the table below. With the exception of the poles, each layer represents a separate 2-sphere, with the equator being a great 2-sphere. The centroids of the 30 equatorial cells form the vertices of an icosidodecahedron
Icosidodecahedron
In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
, with the meridians (as described above) passing through the center of each pentagonal face. The cells labeled "interstitial" in the following table do not fall on meridian great circles.
| Layer # | Number of Cells | Description | Colatitude | Region |
|---|---|---|---|---|
| 1 | 1 cell | North Pole | 0° | Northern Hemisphere |
| 2 | 12 cells | First layer of meridian cells | 36° | |
| 3 | 20 cells | Non-meridian / interstitial / "Tropic of Cancer Tropic of Cancer The Tropic of Cancer, also referred to as the Northern tropic, is the circle of latitude on the Earth that marks the most northerly position at which the Sun may appear directly overhead at its zenith... " |
60° | |
| 4 | 12 cells | Second layer of meridian cells | 72° | |
| 5 | 30 cells | Non-meridian / interstitial | 90° | Equator |
| 6 | 12 cells | Third layer of meridian cells | 108° | Southern Hemisphere |
| 7 | 20 cells | Non-meridian / interstitial / "Tropic of Capricorn Tropic of Capricorn The Tropic of Capricorn, or Southern tropic, marks the most southerly latitude on the Earth at which the Sun can be directly overhead. This event occurs at the December solstice, when the southern hemisphere is tilted towards the Sun to its maximum extent.Tropic of Capricorn is one of the five... " |
120° | |
| 8 | 12 cells | Fourth layer of meridian cells | 144° | |
| 9 | 1 cell | South Pole | 180° | |
| Total | 120 cells | |||
Layers 3 and 7's cells are located directly over the pole cell's vertices. Layer 5's cells are located over the pole cell's edges.
Intertwining rings
The 120-cell can be partitioned into 12 disjoint 10-cell great circle rings, forming a discrete/quantized Hopf fibration. Starting with one 10-cell ring, one can place another ring along side it that spirals around the original ring one complete revolution in ten cells. Five such 10-cell rings can be placed adjacent to the original 10-cell ring. Although the outer rings "spiral" around the inner ring (and each other), they actually have no helical torsion. They are all equivalent. The spiraling is a result of the 3-sphere curvature. The inner ring and the five outer rings now form a six ring, 60-cell solid torus. One can continue adding 10-cell rings adjacent to the previous ones, but it's more instructive to construct a second torus, disjoint from the one above, from the remaining 60 cells, that interlocks with the first. The 120-cell, like the 3-sphere, is the union of these two (CliffordClifford torus
In geometric topology, the Clifford torus is a special kind of torus sitting inside R4. Alternatively, it can be seen as a torus sitting inside C2 since C2 is topologically the same space as R4...
) tori. If the center ring of the first torus is a meridian great circle as defined above, the center ring of the second torus is the equatorial great circle that is centered on the meridian circle.
Also note that the spiraling shell of 50 cells around a center ring can be either left handed or right handed. It's just a matter of partitioning the cells in the shell differently, i.e. picking another set of disjoint great circles.
Other great circle constructs
There is another great circle path of interest that alternately passes through opposing cell vertices, then along an edge. This path consists of 6 cells and 6 edges. Both the above great circle paths have dual great circle paths in the 600-cell. The 10 cell face to face path above maps to a 10 vertices path solely traversing along edges in the 600-cell, forming a decagon. The alternating cell/edge path above maps to a path consisting of 12 tetrahedrons alternately meeting face to face then vertex to vertex in the 600-cell.Orthogonal projections
Orthogonal projections of the 120-cell can be done in 2D by defining two orthonormal basis vectors for a specific view direction.| H4 | - | F4 |
|---|---|---|
[30] |
[20] |
[12] |
| H3 | A2 / B3 / D4 | A3 / B2 |
[10] |
[6] |
[4] |
3-dimensional orthogonal projections can also be made with three orthonormal basis vectors, and displayed as a 3d model, and then projecting a certain perspective in 3D for a 2d image.
3D isometric projection |
Animated 4D rotation |
Perspective projections
These projections use perspective projection, from a specific view point in 4-dimensions, and projecting the model as a 3D shadow. Therefore faces and cells that look larger are merely closer to the 4D viewpoint. Schlegel diagrams use perspective to show 4 dimensional figures, choosing a point above a specific cell, thus making the cell as the envelope of the 3D model, and other cells are smaller seen inside it. Stereographic projectionStereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
use the same approach, but are shown with curved edges, representing the polytope a tiling of a 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
.
A comparison of perspective projections from 3D to 2D is shown in anology.
| Projection | Dodecahedron | Dodecaplex |
|---|---|---|
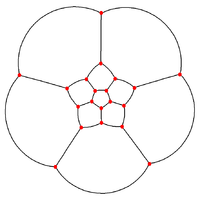
| Schlegel diagram |  12 pentagon faces in the plane |
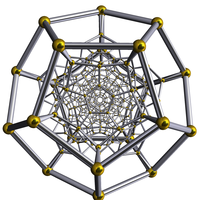 120 dodecahedral cells in 3-space |
| Stereographic projection Stereographic projection The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it... |
 |
 With transparent faces |
| Perspective projection | |
|---|---|
 |
Cell-first perspective projection at 5 times the distance from the center to a vertex, with these enhancements applied:
|
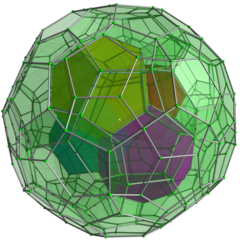 |
Vertex-first perspective projection at 5 times the distance from center to a vertex, with these enhancements:
|
| A 3D projection of a 120-cell performing a simple rotation. | |
| A 3D projection of a 120-cell performing a simple rotation (from the inside). | |
| Animated 4D rotation |
See also
- Uniform polychora family with [5,3,3] symmetry
- 57-cell – an abstract regular polychoronPolychoronIn geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...
constructed from 57 hemi-dodecahedra.
External links
-
- Der 600-Zeller (600-cell) Marco Möller's Regular polytopes in R4 (German)
- 120-cell explorer – A free interactive program that allows you to learn about a number of the 120-cell symmetries. The 120-cell is projected to 3 dimensions and then rendered using OpenGL.
- Construction of the Hyper-Dodecahedron
- YouTube animation of the construction of the 120-cell Gian Marco Todesco.

