B-admissible representation
Encyclopedia
In mathematics
, the formalism of B-admissible representations provides constructions of full Tannakian
subcategories
of the category of representations
of a group
G on finite-dimensional vector space
s over a given field
E. In this theory, B is chosen to be a so-called (E, G)-regular ring, i.e. an E-algebra with an E-linear action of G satisfying certain conditions given below. This theory is most prominently used in p-adic Hodge theory
to define important subcategories of p-adic Galois representations of the absolute Galois group
of local
and global field
s.
s, quotient objects, direct sums, tensor product
s, and duals
.
An (E, G)-ring is a commutative ring
B that is an E-algebra with an E-linear action of G. Let F = BG be the G-invariants of B. The covariant functor DB : Rep(G) → ModF defined by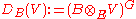
is E-linear (ModF denotes the category of F-modules
). The inclusion of DB(V) in B ⊗EV induces a homomorphism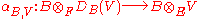
called the comparison morphism.
;for every V in Rep(G), αB,V is injective
;every b ∈ B for which the line bE is G-stable is invertible in B.
The third condition implies F is a field. If B is a field, it is automatically regular.
When B is regular,
with equality if, and only if, αB,V is an isomorphism
.
A representation V ∈ Rep(G) is called B-admissible if αB,V is an isomorphism. The full subcategory of B-admissible representations, denoted RepB(G), is Tannakian.
If B has extra structure, such as a filtration or an E-linear endomorphism
, then DB(V) inherits this structure and the functor DB can be viewed as taking values in the corresponding category.
of G.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the formalism of B-admissible representations provides constructions of full Tannakian
Tannakian category
In mathematics, a tannakian category is a particular kind of monoidal category C, equipped with some extra structure relative to a given field K. The role of such categories C is to approximate, in some sense, the category of linear representations of an algebraic group G defined over K...
subcategories
Subcategory
In mathematics, a subcategory of a category C is a category S whose objects are objects in C and whose morphisms are morphisms in C with the same identities and composition of morphisms. Intuitively, a subcategory of C is a category obtained from C by "removing" some of its objects and...
of the category of representations
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G on finite-dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s over a given field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
E. In this theory, B is chosen to be a so-called (E, G)-regular ring, i.e. an E-algebra with an E-linear action of G satisfying certain conditions given below. This theory is most prominently used in p-adic Hodge theory
P-adic Hodge theory
In mathematics, p-adic Hodge theory is a theory that provides a way to classify and study p-adic Galois representations of characteristic 0 local fields with residual characteristic p . The theory has its beginnings in Jean-Pierre Serre and John Tate's study of Tate modules of abelian varieties and...
to define important subcategories of p-adic Galois representations of the absolute Galois group
Absolute Galois group
In mathematics, the absolute Galois group GK of a field K is the Galois group of Ksep over K, where Ksep is a separable closure of K. Alternatively it is the group of all automorphisms of the algebraic closure of K that fix K. The absolute Galois group is unique up to isomorphism...
of local
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
and global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
s.
(
E, G)-rings and the functor D Let G be a group and E a field. Let Rep(G) denote a non-trivial strictly full subcategory of the Tannakian category of E-linear representations of G on finite-dimensional vector spaces over E stable under subobjectSubobject
In category theory, a branch of mathematics, a subobject is, roughly speaking, an object which sits inside another object in the same category. The notion is a generalization of the older concepts of subset from set theory and subgroup from group theory...
s, quotient objects, direct sums, tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
s, and duals
Dual representation
In mathematics, if G is a group and ρ is a linear representation of it on the vector space V, then the dual representation is defined over the dual vector space as follows:...
.
An (E, G)-ring is a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
B that is an E-algebra with an E-linear action of G. Let F = BG be the G-invariants of B. The covariant functor DB : Rep(G) → ModF defined by
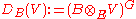
is E-linear (ModF denotes the category of F-modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
). The inclusion of DB(V) in B ⊗EV induces a homomorphism
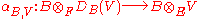
called the comparison morphism.
Regular (
E, G)-rings and B-admissible representations An (E, G)-ring B is called regular ifReduced ring
In ring theory, a ring R is called a reduced ring if it has no non-zero nilpotent elements. Equivalently, a ring is reduced if it has no non-zero elements with square zero, that is, x2 = 0 implies x = 0...
;
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
;
The third condition implies F is a field. If B is a field, it is automatically regular.
When B is regular,
with equality if, and only if, αB,V is an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
.
A representation V ∈ Rep(G) is called B-admissible if αB,V is an isomorphism. The full subcategory of B-admissible representations, denoted RepB(G), is Tannakian.
If B has extra structure, such as a filtration or an E-linear endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
, then DB(V) inherits this structure and the functor DB can be viewed as taking values in the corresponding category.
Examples
- Let K be a field of characteristicCharacteristic (algebra)In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
p (a prime), and Ks a separable closure of K. If E = Fp (the finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
with p elements) and G = Gal(Ks/K) (the absolute Galois group of K), then B = Ks is a regular (E, G)-ring. On Ks there is an injective Frobenius endomorphismFrobenius endomorphismIn commutative algebra and field theory, the Frobenius endomorphism is a special endomorphism of commutative rings with prime characteristic p, an important class which includes finite fields. The endomorphism maps every element to its pth power...
σ : Ks → Ks sending x to xp. Given a representation G → GL(V) for some finite-dimensional Fp-vector space V,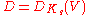
is a finite-dimensional vector space over F=(Ks)G = K which inherits from B = Ks an injective function φD : D → D which is σ-semilinear (i.e. φ(ad) = σ(a)φ(d) for all a ∈ K and all d ∈ D). The Ks-admissible representations are the continuous ones (where G has the Krull topology and V has the discrete topology). In fact, 
is an equivalence of categoriesEquivalence of categoriesIn category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
between the Ks-admissible representations (i.e. continuous ones) and the finite-dimensional vector spaces over K equipped with an injective σ-semilinear φ.
Potentially B-admissible representations
A potentially B-admissible representation captures the idea of a representation that becomes B-admissible when restricted to some subgroupSubgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of G.